
PART IV. SPIRA SOLARIS ARCHYTAS-MIRABILIS

A. THE
FIBONACCI SERIES, PHI-SERIES AND SYNODIC MEAN
That the attested, ubiquitous, and long-revered
constant
Phi = 1.61803398875... - The Golden Mean
provides
the underlying foundations for these exponential planetary functions
should
surprise no one. The value is known to occur in many diverse contexts
that
range from the structure of quasi-crystals,3
Penrose Tiles,4
the
closely related Phi and Fibonacci series,
growth functions, and even the structure of galaxies, our own barred-spiral galaxy, the Milky
Way included, it would seem:
Figure 12. Double-formed* Spira Solaris and the plan-view of the Milky Way
[ Milky Way Plan-view from: Atlas of the Universe ]
* Double-formed In a simplistic sense, the transition from two to three dimensions, i.e., the rotation of two-dimensional Spira Solaris through 180 degrees in both vertical and horizontal planes; the fourth dimension is time itself:-- TIME:- "Eternal, Infinite, Young and Old, and of a Spiral Form." See Part 4d2b: "Spira Solaris and the Three-Fold Number", and a similar process for "Whirlpool" galaxy M51. For an "explanation" concerning the "first motions" and the "first weights" attributed to the Milky Way in antiquity, see the above with accompanying text. Make of it what you will ...
In fact, in 1988,
Timothy Ferris pointed out in Coming of Age in the Milky Way
that: 5
The spiral patterns found inside the chambered nautilus,... are approximated by the Fibonacci Series, an arithmetic operation in which each succeeding unit is equal to the total of the preceding two (1,1,2,3,5,8,...). The ratio created by dividing any number in such a series by the number that follows it approached the value 0.618*. This, not incidentally, is the formula of the "golden section," a geometrical proportion that shows up in the Parthenon, the Mona Lisa, and Botticelli's The Birth of Venus, and is the basis of the octave employed in Western music since the time of Bach. All the fecund diversity of this particular symmetry, expressed in myriad ways from seashells and pine cones to the Well-Tempered Clavier, therefore derives from a single invariance, that of the Fibonacci Series. The realization that one abstract symmetry could have such diverse and fruitful manifestations occasioned delight among Renaissance scholars, who cited it as evidence of the efficacy of mathematics and of the subtlety of God's design. Yet it was only the beginning. Many other abstract symmetries have since been identified in nature - some intact and some "broken," or "flawed," - and their effects appear to extend to the very bedrock foundations of matter and energy. (For an up-to-date, in-depth treatment of this complex topic see: THE GOLDEN RATIO: The Story of Phi, the World's Most astonishing Number, by Mario Livio (Broadway Books, New York, 2002)6
|
Synodics |
|
|
|
(Phi) |
|
|
|
| MERCURY | 0.240843 | 0.240843 | 0.239564 | 0.236068 | -3 | 1 | Ø0 = -1Ø + 1Ø2 |
| Synodic | 0.395794 | 0.389692 | 0.387623 | 0.381966 | -2 | 1.618034 |
Ø1
= 1Ø + 0Ø2
|
| VENUS | 0.615186 | 0.630534 | 0.627187 | 0.618034 | -1 | 2.618034 | Ø2 = 0Ø + 1Ø2 |
| Earth/Synodic | 0.914226 | 1.020226 | 1.014810 | 1.000000 | 0 | 4.236068 | Ø3 = 1Ø + 1Ø2 |
| MARS | 1.880751 | 1.650760 | 1.641996 | 1.618034 | 1 | 6.854102 | Ø4 = 1Ø + 2Ø2 |
| Synodic | 3.124532 | 2.670986 | 2.656806 | 2.618034 | 2 | 11.090170 | Ø5 = 2Ø + 3Ø2 |
| AST. MEAN | 4.724682 | 4.321746 | 4.298802 | 4.236068 | 3 | 17.944272 | Ø6 = 3Ø + 5Ø2 |
| Synodic | 7.849214 | 6.992732 | 6.955608 | 6.854102 | 4 | 29.034442 | Ø7 = 5Ø + 8Ø2 |
| JUPITER | 11.86899 | 11.31448 | 11.25441 | 11.09017 | 5 | 46.978714 | Ø8 = 8Ø + 13Ø2 |
| Synodic | 19.92533 | 18.30721 | 18.21002 | 17.94427 | 6 | 76.013156 | Ø9 = 13Ø + 21Ø2 |
| SATURN | 29.35497 | 29.62168 | 29.46443 | 29.03444 | 7 | 122.991869 | Ø10 = 21Ø + 34Ø2 |
| Synodic | 45.16339 | 47.92889 | 47.67445 | 46.97871 | 8 | 199.005024 | Ø11 = 34Ø + 55Ø2 |
| URANUS | 83.86479 | 77.55058 | 77.13888 | 76.01315 | 9 | 321.996894 | Ø12 = 55Ø + 89Ø2 |
| Synodic | 126.6410 | 125.4794 | 124.8133 | 122.9918 | 10 | 521.001919 | Ø13 = 89Ø + 144Ø2 |
| NEP/PLUTO | 248.2858 | 203.0301 | 201.9522 | 199.0050 | 11 | 842.998814 | Ø14 = 144Ø + 377Ø2 |
|
|
|||||||
|
Synodics |
|
|
|
|
|
|
Decomposition |
| MARS | 1.880751 | 1.650760 | 1.641996 | 1.618034 | 1 | 6.854102 | Ø4 = 1Ø + 2Ø2 |
| Synodic | 2.234889 | 2.670986 | 2.656806 | 1.894427 | "4/3" | 8.024921 | (Ø4/3 = 1.899457) |
| JUPITER | 11.86899 | 11.31448 | 11.25441 | 11.09017 | 5 | 46.978714 | Ø8 = 8Ø + 13Ø2 |
|
Table 3b. The Solar system, Exponential Periods and the Mars-Jupiter Gap |
|||||||

| POSITIONS | Deg | X | PERIOD T, R, V | DISTANCE R | VELOCITY V |
| MERCURY T | 0 | 0 | 0.2360679774997 | 0.3819660112501 | 1.6180339887499 |
| Ura-Sat V | 60 | 0.2771402637873 | 0.4250758357168 | 1.5337931410899 | |
| Saturn V | 120 | 0.3253585116692 | 0.4730511636860 | 1.4539381842480 | |
| Synodic T | 180 | 0.3819660112501 | 0.5264411304099 | 1.3782407724892 | |
| Jupiter V | 240 | 0.4484223664590 | 0.5858568481849 | 1.3064844486040 | |
| Synodic R | 300 | 0.5264411304099 | 0.6519784012656 | 1.2384640249478 | |
| VENUS T | 360 | 1 | 0.6180339887498 | 0.7255626302463 | 1.1739849967053 |
| Venus R | 60 | 0.7255626302463 | 0.8074517950104 | 1.1128629857030 | |
| Mars V | 120 | 0.8517996420792 | 0.8985832154065 | 1.0549232131785 | |
| Earth/Syn. | 180 | 1 | 1 | 1 | |
| Venus V | 240 | 1.1739849967053 | 1.1128629857030 | 0.9479362929050 | |
| Mars R | 300 | 1.3782407724892 | 1.2384640249478 | 0.8985832154065 | |
| MARS T | 360 | 2 | 1.6180339887499 | 1.3782407724892 | 0.8517996420792 |
| Synodic R | 60 | 1.8995476269516 | 1.5337931410899 | 0.8074517950104 | |
| 120 | 2.2300404145684 | 1.7069016144441 | 0.7654128612617 | ||
| Synodic | 180 | 2.6180339887499 | 1.8995476269516 | 0.7255626302463 | |
| 240 | 3.0735326236569 | 2.1139362436145 | 0.6877871499865 | ||
| 300 | 3.6082811870576 | 2.3525213996546 | 0.6519784012656 | ||
| MJ-GM T | 360 | 3 | 4.2360679774998 | 2.6180339887499 | 0.6180339887498 |
| 60 | 4.9730802506086 | 2.9135131213921 | 0.5858568481849 | ||
| 120 | 5.8383216016261 | 3.2423409111574 | 0.5553549688414 | ||
| Synodic | 180 | 6.8541019662497 | 3.6082811870576 | 0.5264411304099 | |
| 240 | 8.0466128742656 | 4.0155225750850 | 0.4990326535935 | ||
| 300 | 9.4466027886838 | 4.4687264420669 | 0.4730511636860 | ||
| JUPITER T | 360 | 4 | 11.0901699437495 | 4.9730802506086 | 0.4484223664590 |
| 60 | 13.0196931248743 | 5.5343569358330 | 0.4250758357168 | ||
| 120 | 15.2849243903099 | 6.1589809835573 | 0.4029448119129 | ||
| Synodic | 180 | 17.9442719099992 | 6.8541019662497 | 0.3819660112501 | |
| 240 | 21.0663059991398 | 7.6276763784735 | 0.3620794447201 | ||
| 300 | 24.7315271789938 | 8.4885587085244 | 0.3432282465651 | ||
| SATURN T | 360 | 5 | 29.0344418537488 | 9.4466027886838 | 0.3253585116692 |
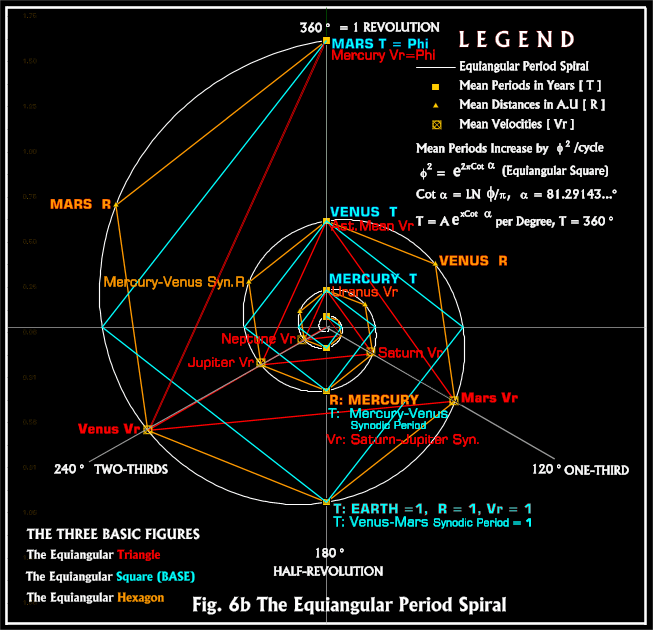
Table 4. The Triadic Equiangular Period
Spiral, Mercury
to Saturn
| POSITIONS | xT | Period T | xR | Distance | xVr | Velocity | xVi |
Inverse
Vi
|
| MERCURY | -3 | 0.2360680 | -6/3 | 0.3819660 | 1 | 1.6180340 | -3/3 | 0.6180340 |
| Synodic 1 | -2 | 0.3819660 | -4/3 | 0.5264411 | 2/3 | 1.3782408 | -2/3 | 0.7255626 |
| VENUS | -1 | 0.6180340 | -2/3 | 0.7255626 | 1/3 | 1.1739850 | -1/3 | 0.8517996 |
| EARTH/Syn | 0 | 1.0000000 | 0 | 1.0000000 | 0 | 1.0000000 | 0 | 1.0000000 |
| MARS | 1 | 1.6180340 | 2/3 | 1.3782408 | -1/3 | 0.8517996 | 1/3 | 1.1739850 |
| Synodic 3 | 2 | 2.6180340 | 4/3 | 1.8995476 | -2/3 | 0.7255626 | 2/3 | 1.3782408 |
| [ MJ-GM ] | 3 | 4.2360680 | 6/3 | 2.6180340 | -3/3 | 0.6180340 | 3/3 | 1.6180340 |
| Synodic 4 | 4 | 6.8541020 | 8/3 | 3.6082812 | -4/3 | 0.5264411 | 4/3 | 1.8995476 |
| JUPITER | 5 | 11.090169 | 10/3 | 4.9730803 | -5/3 | 0.4484224 | 5/3 | 2.2300404 |
| Synodic 5 | 6 | 17.944271 | 12/3 | 6.8541020 | -6/3 | 0.3819660 | 6/3 | 2.6180340 |
| SATURN | 7 | 29.034441 | 14/3 | 9.4466028 | -7/3 | 0.3253585 | 7/3 | 3.0735326 |
| Synodic 6 | 8 | 46.978713 | 16/3 | 13.019693 | -8/3 | 0.2771403 | 8/3 | 3.6082812 |
| URANUS | 9 | 76.013155 | 18/3 | 17.944271 | -9/3 | 0.2360680 | 9/3 | 4.2360680 |
Table 5a. Phi-Series Periods, Distances and Velocities (Mercury-Uranus)
| POSITIONS | xT | Period T | xR | Distance | xVr | Velocity | xVi |
InverseVi
|
| MERCURY | -3 | 0.2360680 | -6/3 | 0.3819660 | 1 | 1.6180340 | -3/3 | 0.6180340 |
| Synodic 1 | -2 | 0.3819660 | -4/3 | 0.5264411 | 2/3 | 1.3782408 | -2/3 | 0.7255626 |
| VENUS | -1 | 0.6180340 | -2/3 | 0.7255626 | 1/3 | 1.1739850 | -1/3 | 0.8517996 |
| Synodic 2 | 1 | 1.6180340 | 1 | 1.3782408 | 2/3 | 0.8517996 | 1/3 | 1.1739850 |
| EARTH | 0 | 1.0000000 | 0 | 1.0000000 | 0 | 1.0000000 | 0 | 1.0000000 |
| Synodic 3 | 2 | 2.6180340 | 4/3 | 1.8995476 | -2/3 | 0.7255626 | 2/3 | 1.3782408 |
| MARS | 1 | 1.6180340 | 2/3 | 1.3782408 | -1/3 | 0.8517996 | 1/3 | 1.1739850 |
| Synodic 4 | 4/3 | 1.8944272 | 4/3 | 1.5310356 | -2/3 | 0.8081786 | 2/3 | 1.2373502 |
| JUPITER | 5 | 11.090169 | 10/3 | 4.9730803 | -5/3 | 0.4484224 | 5/3 | 2.2300404 |
Table 5b. Phi-Series Parameters:
(Mars-Jupiter Mean Omitted)
- The Golden Mean, Phi = 1.618033989.. the limiting value of Fibonacci ratios (Relation 13a).
- - The Fundamental Constant for the Exponential Planetary Framework.
- - The Fundamental constant for the Equiangular Period Spiral.
- The Ordinal numbers (exponents for the mean periods) and all subdivisions.
- The Constant: Pi = 3.141592654...
- The Constant: e = 2.718281828..., the base of natural logarithms
- The Phi-Series
- The Fibonacci Series
- Arithmetic Progressions (Relation 11a)
- Geometric Progressions ( exact for the Phi-Series)
- The Geometric Mean (Relation 11b for the Fibonacci Series)
- The Harmonic Mean (Relation 13b)
- Dual additive Fibonacci series (The phi-series multipliers)
- The Mean Sidereal Periods of Revolution of the Planets
- The Mean Heliocentric Distances of the Planets from the Sun
- The Mean Orbital Velocities and their Inverses
- The Mean Synodic Periods and the Synodic Mean (Relation 12a)
- Velocity Expansions of the Harmonic law
- The Harmonic Law of Planetary motion
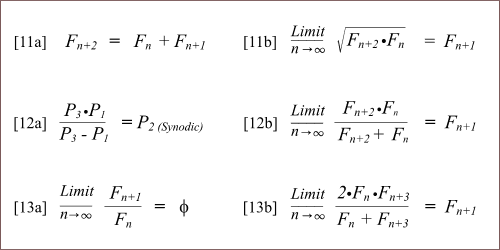
Table 6c. Spira Solaris: Relations 11a through 15b
In light of the above there seems little doubt that in general and in the present astronomical context in particular, Spira Solaris qualifies to be described numerically as "the One and the Many," the "One and the All," "the Alpha and the Omega," and also (from The Chaldean Oracles): "Fountain of Fountains, and of All Fountains, The Matrix of all Things." 8
The latter part of the above
notwithstanding and still remaining with ancient terms and concepts -
in accounting for the
60-degree divisions that provide all three planetary parameters (i.e.,
the
Mean Heliocentric Distances, the Mean Sidereal and Synodic Periods, and
the
mean Orbital Velocities), this increasingly complex Spiral is found to
utilize
the same three fundamental figures known to "fill a space" in
antiquity,
namely the Triangle, the Square and the Hexagon.
As for the part played by Archytas
- an alleged communicator with Plato - it was the same Archytas
who was reputedly:9
"The first who methodically applied the principles of mathematics to mechanics: who imparted an organic motion to a geometric figure, by the section of the semi-cylinder seeking two means that would be proportional, in order to double the cube." [emphasis supplied]
"Hippocrates of Chino (a Pythagorean mathematician) in 440 BC ... declared that the problem could be solved if 2 successive mean proportional line segments were found between a given segment and another twice its length. He gave the equation a : x = x : y = y : 2*a. Hence if a is the side of the original cube, then x = cubic root(2*a) is the side of it's volumetric double. Unfortunately, Hippocrates did not say how the 2 mean proportionals were to be found...."
"TIME: Æternal, Infinite. Young, and Old, of a Spiral Form." (The Chaldean Oracles).The above quotation and rectangular derivation of Phi may be questioned in the exact astronomical contexts suggested here, but despite numerous erudite commentaries both past and present there still remain fundamental ambiguities in many ancient works. Also, and in the case of Plato in particular, as Benjamin Jowett points out: "the obscurity arises from our want of familiarity with the subject," though want of familiarity is hardly limited to this single source. There are many others, and accordingly, difficulties arise from the sheer bulk of available material on one hand and the inordinate amount of groundwork required to assimilate it on the other. Term after term, definition after definition, concept upon concept, some of which may well have have been delivered "synoptically, and in such a way as to be inaccessible to the vulgar" all need to be carefully considered, e.g., the following discussion by Aristotle, who states:11
it is not enough for a definitive formula to express most now do the mere fact; it must include and exhibit the ground also. At present definitions are given in a form analogous to the conclusion of a syllogism, e.g., What is squaring? The construction of an equilateral rectangle equal to a given oblong rectangle. Such a definition is in form equivalent to a conclusion. One that tells us that squaring is the discovery of a line which is a mean proportional between the two unequal sides of the given rectangle discloses the ground of what is defined (Aristotle, On the Soul, Bk II, Chap. 2, 413a, trans. J. A. Smith; emphases supplied)
Simplicius, in his commentary on the 2nd Book of Aristotle, "On the Heavens," remarks that Pythagoras and his followers claimed to have heard the Music of the Spheres, to have heard an harmonic sound produced by the motion of the planets, and from the sound to have calculated by numbers the ratio of distance and size of the Sun, Moon, Venus and Mercury. (W. Wyn Westcott, Numbers, Their Occult Power and Mystic Virtues, Sun Books, Santa Fe, 1983:20-21; emphases supplied)Thus apparently calculations of both "distance" and "size" for not only the Sun and the Moon, but also Venus and Mercury. But why these two inferior planets in particular? One can only theorize (or consider, perhaps, "what is being defined"). But with fundamental units of time provided by the Sun and the Moon it can be seen from the Phi-based planetary framework that there are indeed reasons for linking Venus and Mercury in the above context, i.e., remaining with this pair of planets alone, the parameter Phi-2 = 0.381966011 not only occurs as the mean distance of Mercury, it also occurs as the mean period for the synodic difference cycle between the two planets in question. Thus, from Table 5a, the Mercury-Venus synodic period Phi -2 = the mean distance of Mercury with the latter also readily obtained from (Phi -3) 2/3 = Phi -2 etc.
Proclus further observes that a mirror was assumed by ancient theologists as a symbol of the aptitude of the universe to be filled with intellectual illumination. Hence, says he, they say that Vulcan made a mirror for Bacchus, into which the God, looking and beholding the image of himself, proceeded into the whole divisible fabrication. And you may say that the smoothness of the external surface of the universe, which is mentioned by Plato, reminds us of the above-mentioned catoptric apparatus. (emphases supplied)
D.2.
PYTHAGORAS AND LOGOS
Certainly, once the initial
step towards the Phi-series is taken it is possible
to embark on "the whole divisible fabrication", but there is a further part to the
puzzle
to be included; the constant Phi -2 =
0.381966011, which
in addition to the two assignments already mentioned also occurs as (or
is
mirrored in) the synodic velocity of the Jupiter-Saturn synodic
cycle.
Here with the inclusion of velocity matters become more complex yet
again,
but in technical terms even operations involving fractional exponents
are
not quite as difficult as they might appear (see below.) In any case,
an
early interest in velocity per se is not that easily dismissed;
for
despite the strict oral tradition of the
Pythagorean
School it was nevertheless recorded later that Pythagoras formulated
his instruction
to his followers into:14
two great divisions–the science of numbers and the theory of magnitude. The former division into two branches, arithmetic and musical harmony; the latter was further subdivided into the consideration of magnitude at rest – geometry, and magnitude in motion – astronomy (W. Wyn Westcott, Numbers, Their Occult Power and Mystic Virtues, Sun Books, Santa Fe, 1983:14; emphases supplied)
whereas the content in the second version provided by Burges (1876:153) implies a direct connection between Tetractys and "Soul":16Pythagoras said the sacred Tetractys is: ' the spring having the roots of ever-flowing nature.'
The quotation is exactly as given in the parent publication; the significance of the "Soul" in this context, however, is widened further in the continuation of the first quotation; which is at once simple yet precise:17By my Tetractys, which has given to Soul
The fount, that feeds of ever-flowing Nature
The roots--
Pythagoras said the sacred Tetractys is: ` the spring having the roots of ever-flowing nature.' .... The four parts of the Decad, this perfect number, are called number, monad, power and cube. And the interweavings and minglings of these in the origin of growth are what naturally completes nascent number; for when a power of a power; and a cube is multiplied on a cube, it is the power of a cube; and when a cube is multiplied on a cube, the cube of a cube; thus all numbers, from which arise the genesis of what arises, are seven: number, monad, power, cube, power of a power, power of a cube, and cube of a cube. (Hippol., Phil,. 2. Dox. 355, Pythagorean Sources & Fragments, Kenneth Sylvan Guthrie, Phanes Press, Grand Rapids, Michigan 1988:312; emphases supplied)
But two things alone cannot be satisfactorily united without a third; for there must be some bond between them drawing them together. And of all bonds the best is that which makes itself and the terms it connects a unity in the fullest sense; and it is of the nature of a continued geometrical proportion to effect this most perfectly. For whenever of three numbers, the middle one between any two that are either solids (cubes) or squares is such that, as the first is to it, so is it to the last, and conversely as the last is to the middle, so is the middle to the first, then since the middle becomes first and last, and again the last and first becoming middle, in that way all will necessarily come to play the same part towards one another, and by doing so they will make a unity. Now it had been required that the body of the universe should be a plane surface with no depth, a single measure would have been enough to connect its companions and itself; but in fact the world was to be solid in form, and solids are always conjoined, not be one mean, but by two. Accordingly the god set water and air between fire and earth, and made them, so far as was possible, proportional to one another, so that as fire is to air, so is air to water and as air is to water, so is water to earth, and thus he bounded together the frame of a world visible and tangible. For these reasons and from such constituents, four in number, the body of the universe was brought into being, coming into concord by means of proportion, and from these it acquired Amity, so that coming into unity with itself it became indissoluble by any other save him who bound it together. (Timaeus, 31b-32c, Plato's Cosmology: The Timaeus of Plato, Trans. Francis MacDonald Cornford, Bobbs-Merrill, Indianapolis, 1975:43-44, emphases supplied)Here it is relevant to note that meanings are necessarily influenced by translation; Jowett's version of the above passage, for example, closes with a minor variation of the above that substitutes "friendship" for "amity" but nevertheless continues with the mention of a "perfect whole", whereas Cornford's translation does not:19
And for these reasons and out of such elements which are four in number, the body of the world was created, and it was harmonized by proportion, and therefore has the spirit of friendship, and having been reconciled to itself , it was indissoluble by the hand of any other but the framer.and (again from Jowett), more on the activities of the framer concerning "perfection" and "friendship": 20
Now the creation took up the whole of each of the four elements, for the creator compounded the world out of all the fire and all the water and all the air and all the earth, leaving no parts of any of them nor any power of them outside. His intention was, in the first place, that the animal should be as far as possible a perfect whole and of perfect parts, secondly, that it should be one, leaving no remainders out of which another such world might be created . (Timaeus 32c-33a, Trans. Benjamin Jowett, The Collected Dialogues of Plato, Princeton University Press, Princeton, 1982: 1164, emphases supplied)
he made it smooth and even, having a surface in every direction equidistant from the center, a body entire and perfect, and formed out of perfect bodies. And in the center he put the soul, which he diffused throughout the body, making it also to be the exterior environment of it, and he made the universe a circle moving in a circle, one and solitary, yet by reason of its excellence able to converse with itself, and needing no other friendship or acquaintance. (Timaeus 34a-34b, Trans. Benjamin Jowett, The Collected Dialogues of Plato, Princeton University Press, Princeton, 1982: 1165, emphases supplied)
D2. 2. AMICABLE NUMBERS
In mathematical terms "amity" is perhaps best explained by the first
amicable
pair, 220 and 284--both "amicable" because each
is equal
to the sum of the aliquot parts of the other. Thus 284 equals the sum
of
the aliquot parts of 220 (1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 +
110
= 284) and 220 equals the sum of the aliquot parts of 284 (1 + 2 + 4 +
71
+ 142 = 220). However, neither of these two "amicable" numbers appear
have
any immediately relevance to the Phi-series planetary framework, but
then
again, there remains the reference to unity in the continuation
that
follows, specifically, the statement in Timaeus 34b that:18
"the body of the universe was brought into being, coming into concord by mean of proportion, and from these it acquired Amity, so that coming into unity with itself it became indissoluble by any other save him who bound it together."Here it may be observed that although rarely stated (and also not strictly fulfilling the definition of the term) a form of "amity" undoubtedly exists between unity (1) and the first perfect number (6). In short, while the latter as a "Perfect" number is equal to the sum of its constituent parts (i.e., 1/2 of 6 = 3, 1/3 of 6 = 2, 1/6 of 6 = 1 and 3 + 2 + 1 = 6) unity is in turn the sum of the fractional form of the same set, i.e., the reciprocals, thus 1/2 of 1 = 1/2, 1/3 of 1 = 1/3, 1/6 1 = 1/6 and their sum in turn is 1/2 + 1/3 + 1/6 = 1.
| 1 Mean Heliocentric Distance (R) | = T 2/3 |
| 2 Mean Orbital Velocity (Vr) | = T -1/3 |
| 3 Mean Orbital Velocity (Vr) | = R -1/2 |
| 4 Mean Inverse Velocity (Vi) | = T 1/3 |
| 5 Mean Inverse Velocity (Vi) | = R 1/2 |
| 6 Mean Heliocentric
Distance |
= Vi 2 |
| 7 Mean Sidereal Period (T) | = Vi 3 |
Table 6d. Period, Distance and Velocity Relations
Mean velocities may be
obtained
from the fundamental relationship directly by using negative fractional
exponents
(relations 2 and 3) or more simply from the reciprocals of the inverse
velocities (relations 4 and 5), which are, of course, simply cube
roots
and square roots. Whereas both the distance (R) and the Period (T)
are in turn readily obtained by squaring and cubing the inverse
velocity
(Vi) with all such relations utilizing the integers 1, 2 and
3 in various combinations. Thus the almost perfect amicable pairing
[ 6, 1 ] is hardly numerology, or a simplistic association of
numbers, but
rather an easily learnt mnemonic device that encapsulates a
considerable amount
of information. How far back in time this understanding extends is
difficult
to assess, but these relationships are doubly important, for it is not
only
far easier to obtain the velocities in the above manner, it is also of
historic
significance in addition. Here the reader will recall that the formulas
for
the velocities employed in the construction of the various planetary
frameworks
in Section III were obtained from Galileo, whose
acknowledged
source was in turn Plato (for details see my paper: Projectiles, Parabolas,
and
Velocity Expansions of the Laws of Planetary Motion published
in
the Journal of the Royal Astronomical Society of Canada in 1989 21).
In short, the positive fractional exponents 1/2 and
1/3 gained from the latter play a considerable role in
the computation
of both the mean distances and the mean velocities. Further,
the latter
also produce the inverse velocity components of the Phi-series by
taking
the cube root of the Periods, while squaring the result
in
turn produces the mean distances, i.e., relation 1 above, but in two
distinct
but simpler stages (relations 4 and 6). Lastly, the constant Phi
1/2also provides the basis for
90-degree quadrants
of the equiangular rectangle
underlying the construction of Spira Solaris.
Thus it may not be that surprising that this pair of
fractions--1/2
and 1/3--should together take on historical
significance, as
indeed in the following dense assessment of related matters given by
Francis
McDonald Cornford: 22
We have seen that the whole nature of things, all the essential properties of physis, were believed by the Pythagoreans to be contained in the tetractys of the decad; and it now appears that, just as we should expect, this ' fountain of ever-flowing nature' contains the periodic movement of life, evolving out of unity and reverting to unity again, in the recurrent revolution of a wheel of birth. It embodies the fundamental Dionysiac representation of palingenesia.The occurrence of the "logos or ratio 1/2 or 1/3" (with or without the perfect number 6) appears to be a useful indicator; it occurs, for example, in the final chapter concerning the Fibonacci series and the structure of the Solar System in the Essay on Classification by Louis Agassiz (1857) and it is also elegantly infused into Canon Mosely's 1838 analysis of the spiral structure of the shell Turritella duplicata. It is apparent that the latter's understanding was recognized as such by D'arcy Wentworth Thompson, who in turn provided wider dissemination by repeating the analysis in its essential details in On Growth and Form (1942:773).
But there is something more in it than this. Pythagoras inherited the music of Orpheus, as well as the reincarnation doctrine of Dionysus. From the Orphics he inherited also the doctrine of the fall of the soul from its first perfect state of union with the divine, its degradation into the darkness of this life and of the underworld, and its final restoration to peace and unity. Now, on the model of this doctrine of the fall of the soul, the Pythagorean philosophy must hold that all existence proceeds out of the One and returns to it again; and that the One alone is perfect, while the manifold world of visible body is a turbid medium of appearance, in which the one truth is half-revealed and half-concealed, as the divine soul is manifest in the flesh and yet obscured by it and degraded.
There is thus, inherent in the representation handed down from Orphism to Pythagoras, not only the primitive wheel of birth, but another aspect of the movement of life, which is best described as a processional movement out of unity into plurality, out of light into darkness. This movement, also, must be revealed in the nature of numbers, and contained in the tetractys. Pythagoras found it in the procession of numerical series, the study of which he originated, thereby rounding the science of number. It is practically certain, also, that in music he discovered the ratios of the octave, the fifth, and the fourth, contained in the harmonic proportion 12: 8: 6. Now a progression like those contained in the tetractys of Plato's worldsoul --the series, 1: 2: 4: 8, 1: 3: 9: 27– is what the Pythagoreans called an harmonia; it is a continuous entity knit together by a principle of unity running through it, namely the logos or ratio (1/2 or 1/3) which links every term to its predecessor by the same bond. Both series, moreover, radiate from the One, which in Pythagorean arithmetic was not itself a number, but the source in which the whole nature of all numbers was gathered up and implicit. When we note, further, that every number is not only a many, but also one number, we can see how Pythagoras would find the whole movement of cosmic evolution contained in the procession of series, in which the One passes out of itself into a manifold, yet without losing all its unity, and a return from the many to the One is secured by that bond of proportion which runs, backwards and forwards, through the whole series and links it into a ' harmony.' It is thus that we must understand the doctrine that ' the whole Heaven is harmony and number.' The processional movement of physis is modelled upon that of soul, which falls from its first state of union with the divine, but yet remains linked to the One life by mysterious bonds, and can return to it again, purified by music. (Francis McDonald Cornford, From Religion to Philosophy: A Study in the Origins of Western Speculation, Humanities Press, Atlantic Highlands, 1980:208-210; emphases supplied)
D2.3 DOUBLING THE CUBE
It is at this juncture, i.e., armed with the above, that we may now
revisit Archytas and the puzzling quotation provided earlier, i.e., the
assertion that the latter was: 9
"The first who methodically applied the principles of mathematics to mechanics: who imparted an organic motion to a geometric figure,In addition to what may well be considered a bone fide treatment in terms of conic sections, in the present context by extending the phi-series planetary framework beyond Phi 2 to include the range Phi 3 to Phi 6 and remaining with exponents, it becomes possible to "double the cube" such that ( Phi 3 ) 2 = Phi 6 and thus obtain two mean proportionals between the given limits as a result (i.e., Phi 4 and Phi -5).
by the section of the semi-cylinder seeking two means that would be proportional, in order to double the cube." [emphases supplied]
|
|
|
|
|
|
|
1/3 |
|
|
|
|
|
|
Vi | |
| 3 | Ast./Gap | 4.23606797 | 2.61803398 | 1.61803398 | 0.61803398 | 3/3 |
| 4 | Synodic | 6.85410196 | 3.60828118 | 1.89954762 | 0.52644113 | 4/3 |
| 5 | JUPITER | 11.0901699 | 4.97308025 | 2.23004041 | 0.44842236 | 5/3 |
| 6 | Synodic | 17.9442719 | 6.85410196 | 2.61803398 | 0.38196601 | 6/2 |
| 1 | 2/3 | 1/3 | ||||
| Multipliers | 1.61803398 | 1.37824077 | 1.17398499 |
Table 6e. Phi-Series Planetary Framework Phi 3 to Phi 6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
| 3 | Ast./Gap | 4.23606797 | 2.61803398 | 1.61803398 |
0.6180339
|
6/6 | 3/3 |
|
| 3.5 | 5.38836170 | 3.07353262 | 1.75314934 |
0.5704020
|
7/6 |
|
|
|
| 4 | Synodic | 6.85410196 | 3.60828118 | 1.89954762 |
0.5264411
|
8/6 | 4/3 |
|
| 4.5 | 8.71855238 | 4.23606797 | 2.05817102 |
0.4858682
|
9/6 | -- |
|
|
| 5 | JUPITER | 11.0901699 | 4.97308025 | 2.23004041 |
0.4484223
|
10/6 | 5/3 |
|
| 5.5 | 14.1069140 | 5.83832160 | 2.41626190 | 0.4138624 | 11/6 |
|
|
|
| 6 | Synodic | 17.9442719 | 6.85410196 | 2.61803398 |
0.3819660
|
12/6 | 6/3 |
|
|
|
1/2 | 1/3 | 1/6 | |||||
| Multipliers | 1.27201964 | 1.17398499 | 1.08350588 |
Table 6f. Second augmentation of the Phi-Series Framework Phi 3 to Phi 6
In fact, for additional intervals between planetary positions the halving of the period exponents can be repeated almost indefinitely. Although disarmingly simple, it is clear on examination that this continued division involves the sequence: 1, 1/2, 1/4, 1/8,..., which is in fact the fractional form of Plato's double interval: 1, 2, 4, 8, etc. The resulting tables are not as as forbidding as they might appear either, since all that is necessary for their generation is the latter understanding and the determination of new multipliers for the periods, the distances and also the velocities, which may then be applied to the original planetary data. Thus for Table 6e, for example, the sequential multipliers are 1.61803398, 1.37824077 and 1.17398499 respectively while their square roots are applied in Table 6f, and so on for the "whole divisable fabrication" to proceed, though as it turns out it is the inverse velocities (especially the exponential thirds and sixths) that are of paramount importance as will be seen in later sections.
As for
the
"geometric figure", that we may already have (whether applicable here
or
not) and although the concept of "organic motion" may strike some
modern
readers as strange, it is nevertheless an underlying feature in many
ancient
major works--the Timaeus of Plato especially. Here it may also
be
observed that by expressing the exponents of this short section of the
Phi-series
planetary framework in thirds, the sets [3, 6, 9 , [4, 8, 12]
and [6, 12, 18] are also apparent--sets that may or may not be
considered
further with respect to other passages in Plato, etc. The point being,
of
course, that so far we have only scratched the surface and that there
still
remains a great deal of assimilation and clarification ahead.
Against
this, however, is the amount of potentially relevant material
available,
though origins remain murky.
Lastly,
although
no planet per se exists in the position that corresponds to a
period
of Phi 3 (from a modern viewpoint this
region
is represented by the Mar-Jupiter Gap, or loosely the Asteroid Belt)
the
corresponding mean distance in the Phi-series planetary
framework
is now the fundamental constant Phi 2.
Furthermore,
the same fundamental constant is also the inverse velocity (Vi)
of the Jupiter -Saturn synodic cycle, which (as will also be seen in
later
sections) again turns out to be of some importance.
D2.3
INVERSE VELOCITY AND ANGULAR MOMENTUM
At this point in the proceedings the reader should be aware that the
inverse
velocity in consort with the Period-Distance-Velocity
relationship
T 2 = R 3 = Vr
- 6 provides
substantially
more than mere mathematical convenience. In fact the corresponding
Period-Distance-Inverse Velocity relationship T 2
=
R 3 = Vi - 6
allows Vi to
play a major
role in the computation of planetary angular momentum (L).
A brief description of the latter by Jeffrey K. Wagner is
provided
below:23
Most of the angular momentum of the solar system is in the planets, not in the Sun. This is because the massive Sun rotates very slowly, whereas the planets, less massive but far away, move rapidly enough in their orbits that their angular momentum is greater. This is particularly true for the gas giants. (Angular momentum is a quantity for rotating or revolving objects that is somewhat analogous to momentum for objects moving in a straight line. The angular momentum, L, of an orbiting object is given by the equation L = mav, where m is the mass of the object, a is its semi-major axis, and v is its average orbital velocity. For a rotating object, angular momentum is given by L = Cmr2w, where C is the object's moment of inertia coefficient, m is its mass, r is its radius, and w is its rotational velocity in radians per second. Table 29.1 lists the angular momentum of various solar system objects.) Other important characteristics of the solar system involve the physical properties of its various objects. The planets differ in composition, with the controlling factor being distance from the Sun. The inner, terrestrial planets are rocky and metallic, the outer gas giants are primarily hydrogen and helium, and outermost Pluto is icy. The planets and their satellites resemble miniature solar systems, and most satellites orbit regularly in the equatorial plane of their planet ... (Jeffrey K. wagner; Chap. 29. Constraints on Solar System Formation in Introduction to the Solar System, Holt, Rinehart & Winston, Orlando 1991:426)
Consequently
angular
momentum is essentially the product of the mass, the
mean distance
and the mean velocity. However, because of the relation
Period-Distance-Velocity
relationship: T 2 = R 3
= Vi -6
the
relation: L = Mav may be expressed in the form
Mass x
Vi 2x Vr, which reduces
further to become simply:
Mass
x Vi:
Angular Momentum L = mvi
|
OBJECTS
|
L
(Ang.
M) (g cm2/sec) |
|
Phi-S MVi |
| SUN | 1.6 X 1048 | 0.5% | 0.5% |
| 4 Inner Planets |
4.95 X 1047 | 0.2% | 0.15% |
| Jupiter | 1.9 X 1050 | 60.4% | 60.54% |
| Saturn | 7.8 X 1049 | 24.8% | 24.98% |
| Uranus | 1.7 X 1049 | 5.4% | 5.25% |
| Neptune | 2.6 X 1049 | 8.3% | 8.58% |
| 4 Gas giant Total | 3.14 X 1050 | 98.9% | 99.35% |
Table 6g. Percent Solar
System
L, The Phi-Series Exponential Framework
and the Modern Solar System (after Wagner 1991:426)
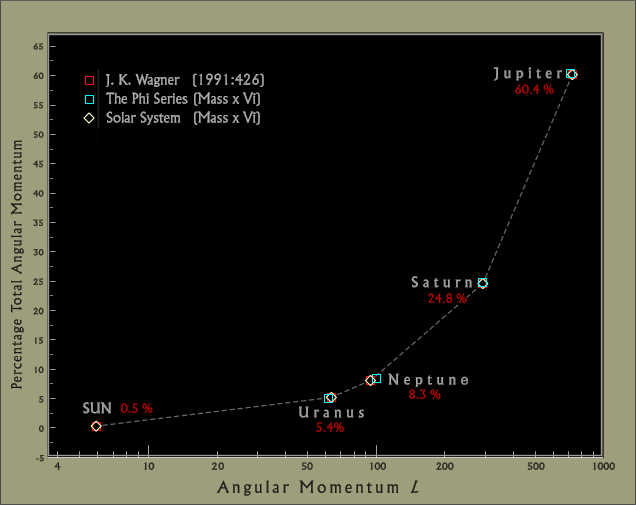
Figure 6c. Angular
Momentum
L. 1: Wagner 1991, 2: The Phi-Series. 3:
Modern
data
D.4.
SOUL, BODY AND SPIRIT: THE ALCHEMICAL ASPECT
The next step--the Alchemical aspect--brings with it difficulty and
controversy,
but hopefully also further enlightenment. Before expanding on this side
of
the matter, however, it may be helpful to remind the reader what was
stressed
in the Overview regarding this subject and ancient sources in general,
namely
that there is potentially an enormous range of material that might be
brought
to bear on the current investigation--so much in fact that at times it
becomes
difficult to separate the gold from the dross, especially without a
distinct
focus. And even with the acquaintance of the parameters of Spira
Solaris,
etc., it is still difficult--not only because of possible degradation
through
time--but also the appropriation and absorption of fundamental
concepts.
Indeed, such is the complexity and continuance of this issue that
readers
should decide for themselves whether "Christian Alchemy" was a valid
appropriation
of an older and more complex understanding, and as such whether it has
been
more a hindrance than a help.
This said, the difference between the two types of
alchemy
is apparent in extant writings, especially instances where alchemists,
after
dedicating their work to the "Father, Son, and Holy Ghost"
nevertheless
reverted to the technical alchemical triad "body, soul and spirit"--a
fundamental
and complex triad that, as we shall see later, is readily understood to
represent
Time, Distance and Velocity in not only astronomical
contexts,
but also in related historical and alchemical contexts in addition.
An example of the shift from the "dedication" to the Father,
Son, and Holy Ghost to the alchemical "body, soul and spirit" is
seen in the first line of following text, which also emphasizes the
metal
Mercury, argent vivre ("Quicksilver"; see below for Phi as the
"Velocity"
of Mercury) while also providing bald references to the four elements
and
not least of all Plato--the latter occurrence again
perhaps
a surprise to some readers.
Thus: "A Treatise of Florianus Raudorff: Of the Stone, or Mercury
of
the Philosophers. In the name of Father, Son, and Holy Ghost. A short
Declaration
of the Great Matter" 24
Chap.1. Know you, that our Medicine is made of three things, viz. of a body, soul and spirit.Bearing in mind that "Soul" has a wide variety of meanings and contexts, and that this was so long before Christian appropriations, consider next the following two passage from Aristotle's On the Soul, and dwell perhaps, not only on the alchemical allusions given here, but also the references to "body", "motion," "harmony", and not least of all intellectual understanding. Thus with respect to these latter aspects Aristotle also writes:25
[Chapters 2 through 5 omitted]
Chap 6. You may say, we do not speak true, that our medicine is made of two things, of body and of spirit; it is right said, that all metals have one root and original.
Chap. 7. Why can it not be made of two compounded together? Answer, 1) They may be made all these together. 2) They must be reduced into a Mercury, which would fall difficult by reason of mans life; therefore we take the next matter, which are the two above said things, viz. the body and spirit: Some Philosophers say in their Books, our medicine is made out of four things, and it is so, for in metals and their spirits are the four Elements; and others say true also, saying, metals must be turned into argent vive: Herein many learned and wise men do err, and lose themselves in this path.
[Chapters 8 through 21 omitted]
Chap. 32. The Philosophers’ Examples. All this being done, then our medicine is finished, and nothing but the ingression is wanting, that the matter may have an ingress into imperfect metals. Plato, and many other Philosophers, begun this work again with dissolving, subliming, or subtiliating, congealing, calcining, as at first, and that medicine which we call a ferment, transmutes Mercury into its nature, in which it is dissolved and sublimed; Philosophers say, our medicine transmutes infinitely imperfect metals; and say that he which attains once to the perfection of it, has no more need of it, to make any more; but they speak it mystically in their expressions." (selections from the Treatise of Florianus Raudorff, Transcribed by Gleb Butuzov from Five Treatises of the Philosophers Stone, London, 1652; emphases supplied)
Some go so far as to hold that the movements which the soul imparts to the body in which it is are the same in kind as those with which it itself is moved. An example of this is Democritus, who uses language like that of the comic dramatist Philippus, who accounts for the movements that Daedalus imparted to his wooden Aphrodite by saying that he poured quicksilver into it; similarly Democritus says that the spherical atoms which according to him constitute soul, owing to their own ceaseless movements draw the whole body after them and so produce its movements. We must urge the question whether it is these very same atoms which produce rest also-how they could do so, it is difficult and even impossible to say. And, in general, we may object that it is not in this way that the soul appears to originate movement in animals-it is through intention or process of thinking.Here then are least hints concerning the astronomical side of the matter; hints that are in addition specifically referred to Plato's Timaeus, along with the "elements" and once again applied intellectual understanding, all further compounded with Pythagorean concepts as follows:26
It is in the same fashion that the Timaeus also tries to give a physical account of how the soul moves its body; the soul, it is there said, is in movement, and so owing to their mutual implication moves the body also. After compounding the soul-substance out of the elements and dividing it in accordance with the harmonic numbers, in order that it may possess a connate sensibility for 'harmony' and that the whole may move in movements well attuned, the Demiurge bent the straight line into a circle; this single circle he divided into two circles united at two common points; one of these he subdivided into seven circles. All this implies that the movements of the soul are identified with the local movements of the heavens. (Aristotle, On the Soul, Bk I, Chap. 3, 406b-407a, trans. J. A. Smith; emphases supplied)
All those, then, who had special regard to the fact that what has soul in it is moved, adopted the view that soul is to be identified with what is eminently originative of movement. All, on the other hand, who looked to the fact that what has soul in it knows or perceives what is, identify soul with the principle or principles of Nature, according as they admit several such principles or one only. Thus Empedocles declares that it is formed out of all his elements, each of them also being soul; his words are:For 'tis by Earth we see Earth, by Water Water,
By Ether Ether divine, by Fire destructive Fire,
By Love Love, and Hate by cruel Hate.In the same way Plato in the Timaeus fashions soul out of his elements; for like, he holds, is known by like, and things are formed out of the principles or elements, so that soul must be so too. Similarly also in his lectures 'On Philosophy' it was set forth that the Animal-itself is compounded of the Idea itself of the One together with the primary length, breadth, and depth, everything else, the objects of its perception, being similarly constituted. Again he puts his view in yet other terms: Mind is the monad, science or knowledge the dyad (because it goes undeviatingly from one point to another), opinion the number of the plane, sensation the number of the solid; the numbers are by him expressly identified with the Forms themselves or principles, and are formed out of the elements; now things are apprehended either by mind or science or opinion or sensation, and these same numbers are the Forms of things. Some thinkers, accepting both premises, viz. that the soul is both originative of movement and cognitive, have compounded it of both and declared the soul to be a self-moving number. ( Aristotle, On the Soul, Bk I, Chap. 2, 404b trans. J. A. Smith; emphases supplied)
Next, consider further the information provided in the Commentaries of Proclus on the Timaeus, especially the reference to "harmony, figure, powers and motion" and the statement that the whole matter is once again: "generated with reference to intellect", followed by the awareness of "soul", then "body," and not least of all, the grouping of "essence, figure, and power, in a three-fold respect" 28since everything is a possible object of thought, mind in order, as Anaxagoras says, to dominate, that is, to know, must be pure from all admixture; for the co-presence of what is alien to its nature is a hindrance and a block: it follows that it too, like the sensitive part, can have no nature of its own, other than that of having a certain capacity. Thus that in the soul which is called mind (by mind I mean that whereby the soul thinks and judges) is, before it thinks, not actually any real thing. For this reason it cannot reasonably be regarded as blended with the body: if so, it would acquire some quality, e.g. warmth or cold, or even have an organ like the sensitive faculty: as it is, it has none. It was a good idea to call the soul 'the place of forms', though (1) this description holds only of the intellective soul, and (2) even this is the formsonly potentially, not actually (Aristotle, On the Soul, Bk III, Chap. 4, 429a, trans. J. A. Smith; emphases supplied). 27
Since Plato gives to the soul afterward, all such things as he before gave to the body, viz. essence, harmony, figure, powers, and motion, and conjoins both to the completion of one animal; in order that you may not ignorantly suppose that body and soul are of a similar dignity, being deceived by homonymous appellations, he concisely reminds us of the difference between the two, and does not superfluously say, that body is visible, but soul is invisible; and shows that body is the object of opinion, because it is sensible and generated, but that the soul is unbegotten, as with reference to the body, but generated as with reference to intellect. For it belongs at one and the same time to eternal beings, and generated natures, but it is the last of the former; since time has now a place in it. (The Commentaries of Proclus on the Timaeus of Plato, translated from the Greek by Thomas Taylor, Vol. 2, Bk III, p.154, Kessinger, Kila, ISBN 1-56459-349-5; emphases supplied)What then is "Soul," "Body" and "Spirit" in the above contexts? From an astronomical viewpoint the reader is asked to bear in mind that as far as the planets are concerned it is only the mean periods of revolution (T) that are observable, but it is the planets that are visible; that both the mean distances (R) and the mean velocities (V) must be obtained by intellection, i.e., from the application of the Harmonic Law and its associated variants, thus the mean distance R from T2/3 and the mean velocity V from T -1/3 etc. Or, remaining with positive roots, the reciprocal of the inverse velocity. But in any event, as discussed further in later sections TIME may reasonably be represented by "Soul", DISTANCE by "Body," and VELOCITY by "Spirit" as assigned in Table 5c. The table--which extends from the Inter-Mercurial Object (IMO) to Uranus for completeness, thus embracing all the visible planets and also the dual occurrence of the value 0.2360680 --is colour-coded to enhance the three-fold nature of the Phi-series planetary framework.And if it be requisite to speak clearly, what appears to me to be the case, harmony must be conceived to have three-fold subsistance; so as to be, either harmony itself, or that which is first harmonized; being a thing of this kind according to the whole of itself; or that which is secondarily harmonized, and in a certain respect participates in harmony. And the first of these must be assigned to intellect; the second to soul; and the third to body. The rational, likewise, or reasoning energy, has a three-fold subsistence; the first being primordial; the second according to participation; and the third according to representation or resemblance. For there is also a certain vestige of the rational energy, in some irrational animals. We likewise understand essence, figure, and power, in a three-fold respect. For essence according to its primary subsistence, and the first figure, and the first power, are intelligibles. (The Commentaries of Proclus on the Timaeus of Plato, translated from the Greek by Thomas Taylor, Vol. 2, Bk III, pp.155-56, Kessinger, Kila, ISBN 1-56459-349-5) 29
PLANETS
SynodicsxT PhixPERIODS
T: SoulxR PhixDISTANCE R: Body xV PhixVELOCITY V: Spirit xVi
PhixINVERSE
ViI.M.O -5 Synodic -4 MERCURY -3 0.2360680 0.3819660 1.6180340 0.6180340 Synodic -2 0.3819660 0.5264411 1.3782408 0.7255626 VENUS -1 0.6180340 0.7255626 1.1739850 0.8517996 Earth/Syn 0 1.0000000 1.0000000 1.0000000 MARS 1 1.6180340 1.3782408 0.8517996 1.1739850 Synodic 2 2.6180340 0.7255626 1.3782408 MJ-MEAN 3 4.2360680 0.6180340 1.6180340 Synodic 4 6.8541020 3.6082812 0.5264411 1.8995476 JUPITER 5 11.090169 4.9730803 2.2300404 Synodic 6 17.944271 6.8541020 0.3819660 2.6180340 SATURN 7 29.034441 9.4466028 0.3253585 3.0735326 Synodic 8 46.978713 13.019693 0.2771403 3.6082812 URANUS 9 76.013155 17.944271 0.2360680 4.2360680 Table 5c. Phi-Series Periods, Distances, Velocities and Three-fold Numbers
83. The Circulation of the Elements is performed by a double Whorl, by the greater or extended, and the less or contracted. The Whorl extended fixeth all the Elements of the Earth, and its circle is not finished unless the work of Sulphur be perfected. The revolution of the minor Whorl is terminated by the extraction and preparation of every Element. Now in this Whorl there are three Circles placed, which always and variously move the Matter, by an Erratic and Intricate Motion, and do often (seven times at least) drive about every Element, in order succeeding one another, and so agreeable, that if one shall be wanting the labour of the rest is made void. These Circulations are Nature's Instruments, whereby the Elements are prepared. Let the Philosopher therefore consider the progress of Nature in the Physical Tract [note 49." See the Enchiridion in Manget's Bibliotheca, liber. II., section 3."], more fully described for this very end. (W. Wynn Westcott, "Hermetic Arcanmum of Penes Nos Unda Tagi", Collectanea Hermetica, Kessinger, Kila, ISBN 1-56459-260-X, p.33)Lastly, in view of the introductory steps taken so far, readers may wish to consider the implications of the following passage from Plato's Epinomis concerning education, knowledge and applied intellection, either in general, in the present context, or not at all--each according to the reader's choice and understanding:32
.... there will be a need for several sciences. The first and most important of them is likewise that which treats of pure numbers--not numbers concreted in bodies, but the whole generation of the series of odd and even, and the effects which it contributes to the nature of things. When all this has been mastered, next in order comes what is called by the very ludicrous name mensuration, but is really a manifest assimilation to one another of numbers which are naturally dissimilar, effected by reference to areas. Now to a man who can comprehend this, it will be plain that this is no mere feat of human skill, but a miracle of God's contrivance. Next, numbers raised to the third power and thus presenting an analogy with three-dimensional things. Here again he assimilates the dissimilar by a second science, which those who hit on the discovery have named stereometry [the gauging of solids], a device of God's contriving which breeds amazement in those who fix their gaze on it and consider how universal nature molds form and type by the constant revolution of potency and its converse about the double in the various progressions. The first example of this ratio of the double in the advancing number series is that of 1 to 2; double of this is the ratio of their second powers [ 4 ], and double of this again the advance to the solid and tangible, as we proceed from 1 to 8 [ 1, 2, 2 2, 23]; the advance to a mean of the double, that mean which is equidistant from lesser and greater term [the arithmetical], or the other mean [the harmonic] which exceeds the one term and is itself exceeded by the other by the same fraction of the respective terms--these ratios of 3 : 2 and 4 : 3 will be found as means between 6 and 2: why, in the potency of the mean between these terms [ 6 x 2 ], with its double sense, we have a gift from the blessed choir of the Muses to which mankind owes the boon of the play of consonance and measure, with all they contribute to rhythm and melody.Undoubtedly the more this matter is investigated the more complex it becomes. Nevertheless, we do know a definite method that produces two mean proportionals--mean proportionals, moreover, that are also successive members of the Phi-Series planetary framework. As for the space-filling three basic figures, these also occur somewhat surprisingly in the writings of the medieval scholar Nicole Oresme [1328-1382 CE], who for his part saw fit to include references to Archimedes and a spiral in his own work. The latter also attached considerable weight to the insights provided by the Arab scholar Ibn Rushd [Averroes 1128 CE - 1198 CE] and it is to these relatively neglected sources that we turn next for further enlightenment.
So much, then, for our program as a whole. But to crown it all, we must go on to the generation of things divine, the fairest and most heavenly spectacle God has vouchsafed to the eye of man. And: believe me, no man will ever behold that spectacle without the studies we have described, and so be able to boast that he has won it by an easy route. Moreover, in all our sessions for study we are to relate the single fact to its species; there are questions to be asked and erroneous theses to be refuted. We may truly say that this is ever the prime test, and the best a man can have; as for tests that profess to be such but are not, there is no labor so fruitlessly thrown away as that spent on them. We must also grasp the accuracy of the periodic times and the precision with which they complete the various celestial motions, and this is where a believer in our doctrine that soul is both older and more divine than body will appreciate the beauty and justice of the saying that ' all things are full of gods ' and that we have never been left unheeded by the forgetfulness or carelessness of the higher powers. There is one observation to be made about all such matters. If a man grasps the several questions aright, the benefit accruing to him who thus learns his lesson in the proper way is great indeed; if he cannot, 'twill ever be the better course to call on God. Now the proper way is this--so much explanation is unavoidable. To the man who pursues his studies in the proper way, all geometric constructions, all systems of numbers, all duly constituted melodic progressions, the single ordered scheme of all celestial revolutions, should disclose themselves, and disclose themselves they will, if, as I say, a man pursues his studies aright with his mind's eye fixed on their single end. As such a man reflects, he will receive the revelation of a single bond of natural interconnection between all these problems. If such matters are handled in any other spirit, a man, as I am saying, will need to invoke his luck. We may rest assured that without these qualifications the happy will not make their appearance in any society; this is the method, this the pabulum, these the studies demanded; hard or easy, this is the road we must tread. (Epinomis, 989d-992a, Trans. A.E. Taylor, The Collected Dialogues of Plato, Princeton University Press, Princeton, 1982:1530-31; original square brackets; bold and italic emphases supplied)
IVd2 Spira Solaris and the Middle Ages
http://www.spirasolaris.ca/sbb4d2.htmlIVd3 Spira Solaris: The Fourth Planet and Fifth Element.
http://www.spirasolaris.ca/sbb4d3.htmlIVe Spira Solaris: The Chaldean Oracles, Proclus, and Johannes Kepler
http://www.spirasolaris.ca/sbb4e.html
IVf Spira Solaris and the Universal Ouroborus
http://www.spirasolaris.ca/sbb4e.html
For more
on the phyllotaxic side of the matter, see:
THE THREE-FOLD NUMBER
IVd2b Spira Solaris and the 3-Fold Number
http://www.spirasolaris.ca/sbb4d2b.html
The Spiral of Pheidias; Pheidian/Golden Spirals Defined.
Pheidian Spirals and the Chemical Elements.
The Phyllotaxic approach to the structure of the Solar System of Benjamin Pierce (1750)
THE PHEIDIAN PLANORBIDAE
IVd2c Spira Solaris and the Pheidian Planorbidae.
http://www.spirasolaris.ca/sbb4d2c.html Applied to Nautiloid spirals, Ammonites, Snails and Seashells.
Whirling Rectangles and Double spiral forms; The Phedian Planorbidae in Astronomical context;
Orbital velocity, Inverse Velocity, Mass and Angular Momentum.
The real-time motions of Jupiter and Saturn and the fundamental growth constant 0.381966011
Appendix: The Matter of Lost Light.The understanding of Canon Mosely and Sir D'Arcy Wentworth Thompson.
REFERENCES
Copyright © 1997. John N. Harris, M.A. (CMNS). Last Updated on June 4, 2003.