
PART VIb. SPIRA SOLARIS AND THE MIDDLE AGES

A. NICOLE ORESME (1323-1382 CE)
It seems appropriate to begin this next section with a quotation from Ovid provided by Nicole Oresme in his major work, Le livre du ciel et du monde:
"The three-fold number is present in all things whatsoever; nor did we ourselves discover this number, but rather nature teaches it to us"
Written between 1370 and 1375 CE - some two and a half centuries before Galileo's censure for asserting that Earth was in motion - Le livre du ciel et du monde (hereafter referred to as Du Ciel ) includes a detailed discussion of the issue, the opinion of Heraclides Ponticus: "that the earth moves circularly and that the heavens remain at rest," and Oresme's cautious assessment: "subject, of course, to correction, it seems to me that it is possible to embrace the argument and consider with favour the conclusions set forth in the above opinion that the heavens has a diurnal or daily rotation." Moreover, anticipating Copernicus, Oresme finally concluded: "after considering all that has been said, one could then believe that the earth moves and not the heavens, for the opposite is not clearly evident." This remains one of the better known passages in Du ciel; its implications and the generous latitude permitted Oresme suggests, however, that this source might provide a useful starting point for our present inquiry.
Although Du Ciel was ostensively a commentary and a translation of Aristotle's De Caelo from medieval Latin into French, as the contents attest, it was clearly far more than this, for it also embraced Plato's cosmology and included three additional chapters by Oresme himself. In the introduction to his English translation of Du Ciel, Albert D. Menut describes it as a work that:
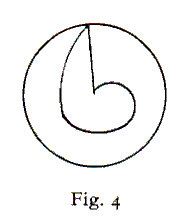
ranges over a vast field of subjects, dealing with the physical and cosmological speculations of the original text. Sometimes Oresme points out an inconsistency between a passage in De caelo and a related Aristotlean text, most frequency in the Physics. Again, he explains the terse language of Aristotle analytically, in simple terms that an educated layman might be expected to comprehend, with examples drawn from concrete instances in nature or easily observed experience.... Often he finds himself at odds with the principle expressed in the text; on such occasions - and they are numerous - we may expect an extended comment involving skillful discussion of abstruse problems - the character of a continuum, the existence of a vacuum, infinity and indivisible, the nature and the laws of motion, the measure of velocities, the plurality of worlds, the rotation of the earth, the intensification and remission of qualities - these and many other subjects that challenged the best thought of fourteenth-century science received thoughtful treatment in Oresme's commentary. (Albert D. Menut, 1968:4; emphases supplied)Of immediate interest here is the inclusion of the laws of motion, and especially the "measure" of velocities. Nevertheless, it is still surprising to discover that Oresme deemed it necessary to discus motion in terms of a spiral to the extent that he even included a diagram (see Fig.4 below from Du Ciel; Albert Menut,1986:65):
Here are two things which require clarification. One is to explain the characteristics of mixed movement; such motion is neither purely straight nor purely circular. Generally speaking, this mixture may be of three kinds. One is composed of several varieties of rectilinear motion and the other of several kinds of circular motion and the third of both rectilinear and circular or of several such compound motions. ... an example of the second kind of motion [circular] is the daily movement of the planets; as with the sun, whose motion is mixed, being involved in the daily movement of the heavens and in the proper movement of its own sphere, and this applies to planets also. The compound movements are not limited to two kinds of circular motion but may be several, some more, some less. Of the third kind of motion [rectilinear and circular mixed], and example would be the movement of an object upon the semi-diameter [or radius] of a circle when the radius is moved circularly. Such a motion describes a line called helix, which Archimedes uses in his demonstration of the squaring of a circle and a typical helix is shown here in a drawing.." [Du Ciel, Book I, Chapter 3, fols. 8c-8d. pp.63-65.]
The above passage may be compared with the following expositions concerning rectilinear and circular motion also given in the Commentaries of Proclus on the Timeus of Plato:
The figure of the spiral likewise, is no vain, fortuitous things, but gives completion to the media between bodies that move in right lines, and those that are moved in a circle. For the circle alone, as we have said, is in the inerratic sphere, but the right line in generation. And the spiral is in the planetary region, as having a co-mixture of the periphery and the right line. The motions also according to breadth and according to depth, viz. of the upward and downward, and the oblique motions. Perhaps likewise, the theurgist [Julian] in celebrating time as a spiral form, as both young and old, directed his attention to this, conceiving that the temporal periods, were especially to be known through the motions of the planets. [Trans. Thomas Taylor, Vol. II, Book IV, p.239]
With these things however, not only Plato as we have observed, but theurgists likewise accord. For they celebrate time as a mundane God, eternal, boundless, young and old, and of a spiral form. And besides this also, as having its essence in eternity, as abiding always the same, and as possessing infinite power. For how could it otherwise comprehend the infinity of apparent time, and circularly lead all things to their former condition, and renovate them, and also recall things which become old through it, to their proper measure, as being at once comprehensive both of things that are moved in a circle, and according to a right line. For a spiral is a thing of this kind; and hence, as I have before observed, time is celebrated by theurgists, as having a spiral form. [trans. Thomas Taylor, Vol. II, Book IV, pp.207-8, emphasis supplied]Here we may make take a further cue from Oresme's mention of Archimedes in this context while at the same time recognizing the necessity for the initial determinination of the "temporal periods" of revolution (as Proclus calls them) from which all else follows, the heliocentric concept included. Furthermore, in preparation for what is to follow next we need also to recall not only the salient features of Spira Solaris - the equiangular period spiral derived in the previous section - but also the various degrees of complexity that accompany it. In particular, it is necessary to recall that it is unequivocably heliocentric. Secondly, while the periods of revolution predominate in both the construction and the final format (the mean sidereal periods at the 360-degree position and the mean synodic positions at 180 degrees) the Spiral - the "Alpha and the Omega", the "One and the Many" - additionally embraces both the mean heliocentric distances and the mean relative orbital velocities. Especially noteworthy here are the latter parameters for Venus, Mars, Jupiter, Saturn, (and Neptune) which occur at either the 120 or 240-degree points on the Spiral, i.e., at the ONE-THIRD or TWO-THIRDS locations. With this in mind we may now follow Oresme's lead and consider whether the extant work of Archimedes on the spiral sheds any further light on this increasingly complex matter.
Now you are aware that 'universe' is the name given by most astronomers to the sphere whose centre is the centre of the earth and whose radius is equal to the straight line between the centre of the sun and the centre of the earth. This is the common account, as you have heard from astronomers. But Aristarchus of Samos brought out a book consisting of some hypotheses, in which the premisses lead to the result that the universe is many times greater than that now so called. His hypotheses are that the fixed stars and the sun remain unmoved, that the earth revolves about the sun in the circumference of a circle, the sun lying in the middle of the orbit, and that the sphere of the fixed stars, situated about the same centre as the sun, is so great that the circle in which he supposes the earth to revolve bears such a proportion to the distance of the fixed stars as the centre of the sphere bears to its surface. Now it is easy to see that this is impossible; for, since the centre of the sphere has no magnitude, we cannot conceive it to bear any ratio whatever to the surface of the sphere. We must however take Aristarchus to mean this: since we conceive the earth to be, as it were, the centre of the universe, the ratio which the earth bears to what we describe as the 'universe' is the same as the ratio which the sphere containing the circle in which he supposes the earth to revolve bears to the sphere of the fixed stars. For he adapts the proofs of his results to a hypothesis of this kind, and in particular he appears to suppose the magnitude of the sphere in which he represents the earth as moving to be equal to what we call the 'universe.' I say then that, even if a sphere were made up of the sand, as great as Aristarchus supposes the sphere of the fixed stars to be, I shall still prove that of the numbers named in the Principles, some exceed in multitude the number of the sand which is equal in magnitude to the sphere referred to, provided that the following assumptions be made." [THE WORKS OF ARCHIMEDES INCLUDING THE METHOD translated by Sir Thomas Heath, GREAT BOOKS OF THE WESTERN WORLD #11, Robert Maynard Hutchins, Editor in chief, William Benton, Chicago, 1952:520, emphases supplied.]A second misconception is that Archimedes and to some extent the Ancient Greeks in general were not greatly concerned with practical applications. But this again may be weighed against the written record - in the first instance as summarized by Sir Thomas Heath in his Introduction to THE WORKS OF ARCHIMEDES:
ARCHIMEDES was a citizen of Syracuse, in Sicily, where he was born around the year 287 B.C. He was intimate with Hiero, King of Syracuse, and with his son, Gelo, and Plutarch says that he was related to them. In his Sand-Reckoner, which was dedicated to Gelo, Archimedes speaks of his father, Pheidias, as an astronomer who investigated the sizes and distances of the sun and moon. As a young man Archimedes seems to have spent some time in Egypt, where he invented the water-screw as a means of drawing water out of the Nile for irrigating the fields, though it is also said that he invented this machine to drain bilge water from a huge ship built for King Hiero. He may have studied with the pupils of Euclid in Alexandria. It was probably there that he made the friendship of Conon of Samos and Eratosthenes. To Conon he was in the habit of communicating his discoveries before their publication, and it was for Eratosthenes that he wrote the Method and through him that he addressed the famous Cattle-Problem to the mathematicians of Alexandria--if the tradition is to be credited that associates Archimedes with this problem. After the death of Conon, Archimedes sent his discoveries to Conon's friend and pupil, Dositheus of Pelusium, to whom four of the extant treatises are dedicated. His mechanical inventions won great fame for Archimedes and figure largely in the traditions about him. After discovering the solution of the problem To move a given weight by a given force, he boasted to King Hiero: "Give me a place to stand on and I can move the earth." Asked for a practical demonstration, he contrived a machine by which with the use of only one arm he drew out of the dock a large ship, laden with passengers and goods, which the combined strength of the Syracusans could scarcely move. From that day Hiero ordered that "Archimedes was to be believed in everything he might say." At the king's request Archimedes then made for him catapults, battering rams, cranes, and many other engines of war, which were later used with such success in the defense of Syracuse against the Romans that they were unable to take the city except by treachery. There is also a story in Lucian that Archimedes set fire to the Roman ships by an arrangement of burning glasses. Although Archimedes acquired by his mechanical inventions "the renown of more than human sagacity," according to Plutarch, he "would not deign to leave behind him any commentary or writing on such subjects," since he considered them "sordid and ignoble." He did, however, write a description, now lost, of an apparatus, composed of concentric glass spheres moved by water power, representing the Eudoxian system of the world. This astronomical machine, which survived to be seen and described by Cicero in his Republic, was sufficiently accurate to show the eclipses of the sun and the moon. Except for this lost work On Sphere-making, Archimedes wrote only on strictly mathematical subjects. He took all the mathematical sciences for his province: arithmetic, geometry, astronomy, mechanics, and hydrostatics. Unlike Euclid and Apollonius he wrote no textbooks. Of his writings, although some have been lost, the most important have survived. The absorption of Archimedes in his mathematical investigations was so great that he forgot his food and neglected his person, and when carried by force to the bath, Plutarch records, "he used to trace geometrical figures in the ashes of the fire and diagrams in the oil on his body." Asked by Hiero to discover whether a goldsmith had alloyed with silver the gold of his crown, Archimedes found the answer while bathing by considering the water displaced by his body, whereupon he is reported to have run home in his excitement without his clothes, shouting, "Eureka" (I have found it). Archimedes' preoccupation with mathematics is even said to have been the cause of his death. In the general massacre which followed the capture of Syracuse by Marcellus in 212 B.C., Archimedes was so intent upon a mathematical diagram that he took no notice, and when ordered by a soldier to attend the victorious general, he refused until he should have solved his problem, whereupon he was slain by the enraged soldier. [THE WORKS OF ARCHIMEDES INCLUDING THE METHOD translated by Sir Thomas Heath, GREAT BOOKS OF THE WESTERN WORLD #11, Robert Maynard Hutchins, Editor in chief, William Benton, Chicago, 1952:399-400, emphases supplied]The last paragraph contains a point of particular interest, for although the death of Archimedes as described above is almost universally accepted, an interesting variant by Plutarch describes something altogether different - again with the emphasis on the practical side, for Plutarch relates in Marcellus that: "Archimedes was carrying to Marcellus mathematical instruments, dials, spheres, and angles, by which the magnitude of the sun might be measured to the sight, some soldiers seeing him, and thinking that he carried gold in a vessel, slew him". The circumstances leading up to the death of Archimedes are however preceded by an account of the various machines of war designed by Archimedes in the defence of Syracuse - machines that:
"he had designed and contrived, not as matters of any importance, but as mere amusements in geometry; in compliance with King Hiero's desire and request, some little time before, that he should reduce to practice some part of his admirable speculation in science, and by accommodating the theoretic truth to sensation and ordinary use, bring it more within the appreciation of the people in general."Plutarch next provides a blow by blow account of the defense of Syracuse and the devastation wrought by the weapons built by Archimedes. However, the account is also noteworthy for unexpected references to both mean proportion and Archytas, and also a line better suited to Plato's Timaeus or the Chaldean Oracles than a description of a battle ("the body of Archimede's designs, one soul moving and governing all"). Returning to the text itself, Plutarch continues with his historical aside as follows:
Eudoxus and Archytas had been the first originators of this far-famed and highly-prized art of mechanics, which they employed as an elegant illustration of geometrical truths, and as means of sustaining experimentally, to the satisfaction of the senses, conclusions too intricate for proof by words and diagrams. As, for example, to solve the problem, so often required in constructing geometrical figures, given the two extremes, to find the two mean lines of a proportion, both these mathematicians had recourse to the aid of instruments, adapting to their purpose certain curves and sections of lines. But what with Plato's indignation at it, and his invectives against it as the mere corruption and annihilation of the one good of geometry, which was thus shamefully turning its back upon the unembodied objects of pure intelligence to recur to sensation, and to ask help (not to be obtained without base supervisions and depravation) from matter; so it was that mechanics came to be separated from geometry, and, repudiated and neglected by philosophers, took its place as a military art. Archimedes, however, in writing to King Hiero, whose friend and near relation he was, had stated that given the force, any given weight might be moved, and even boasted, we are told, relying on the strength of demonstration, that if there were another earth, by going into it he could remove this. Hiero being struck with amazement at this, and entreating him to make good this problem by actual experiment, and show some great weight moved by a small engine, he fixed accordingly upon a ship of burden out of the king's arsenal, which could not be drawn out of the dock without great labour and many men; and, loading her with many passengers and a full freight, sitting himself the while far off, with no great endeavour, but only holding the head of the pulley in his hand and drawing the cords by degrees, he drew the ship in a straight line, as smoothly and evenly as if she had been in the sea. The king, astonished at this, and convinced of the power of the art, prevailed upon Archimedes to make him engines accommodated to all the purposes, offensive and defensive, of a siege. These the king himself never made use of, because he spent almost all his life in a profound quiet and the highest affluence. But the apparatus was, in most opportune time, ready at hand for the Syracusans, and with it also the engineer himself.
When, therefore, the Romans assaulted the walls in two places at once, fear and consternation stupefied the Syracusans, believing that nothing was able to resist that violence and those forces. But when Archimedes began to ply his engines, he at once shot against the land forces all sorts of missile weapons, and immense masses of stone that came down with incredible noise and violence; against which no man could stand; for they knocked down those upon whom they fell in heaps, breaking all their ranks and files. In the meantime huge poles thrust out from the walls over the ships sunk some by the great weights which they let down from on high upon them; others they lifted up into the air by an iron hand or beak like a crane's beak and, when they had drawn them up by the prow, and set them on end upon the poop, they plunged them to the bottom of the sea; or else the ships, drawn by engines within, and whirled about, were dashed against steep rocks that stood jutting out under the walls, with great destruction of the soldiers that were aboard them. A ship was frequently lifted up to a great height in the air (a dreadful thing to behold), and was rolled to and fro, and kept swinging, until the mariners were all thrown out, when at length it was dashed against the rocks, or let fall. At the engine that Marcellus brought upon the bridge of ships, which was called Sambuca, from some resemblance it had to an instrument of music, while it was as yet approaching the wall, there was discharged a piece of rock of ten talents weight, then a second and a third, which, striking upon it with immense force and a noise like thunder, broke all its foundation to pieces, shook out all its fastenings, and completely dislodged it from the bridge. So Marcellus, doubtful what counsel to pursue, drew off his ships to a safer distance, and sounded a retreat to his forces on land. They then took a resolution of coming up under the walls, if it were possible, in the night; thinking that as Archimedes used ropes stretched at length in playing his engines, the soldiers would now be under the shot, and the darts would, for want of sufficient distance to throw them, fly over their heads without effect. But he, it appeared, had long before framed for such occasions engines accommodated to any distance, and shorter weapons; and had made numerous small openings in the walls, through which, with engines of a shorter range, unexpected blows were inflicted on the assailants. Thus, when they who thought to deceive the defenders came close up to the walls, instantly a shower of darts and other missile weapons was again cast upon them. And when stones came tumbling down perpendicularly upon their heads, and, as it were, the whole wall shot out arrows at them, they retired. And now, again, as they were going off, arrows and darts of a longer range inflicted a great slaughter among them, and their ships were driven one against another; while they themselves were not able to retaliate in any way. For Archimedes had provided and fixed most of his engines immediately under the wall; whence the Romans, seeing that indefinite mischief overwhelmed them from no visible means, began to think they were fighting with the gods.
Yet Marcellus escaped unhurt, and deriding his own artificers and engineers, "What," said he, "must we give up fighting with this geometrical Briareus, who plays pitch-and-toss with our ships, and, with the multitude of darts which he showers at a single moment upon us, really outdoes the hundred-handed giants of mythology?" And, doubtless, the rest of the Syracusans were but the body of Archimedes's designs, one soul moving and governing all; for, laying aside all other arms, with this alone they infested the Romans and protected themselves. In fine, when such terror had seized upon the Romans, that, if they did but see a little rope or a piece of wood from the wall, instantly crying out, that there it was again, Archimedes was about to let fly some engine at them, they turned their backs and fled, Marcellus desisted from conflicts and assaults, putting all his hope in a long siege. Yet Archimedes possessed so high a spirit, so profound a soul, and such treasures of scientific knowledge, that though these inventions had now obtained him the renown of more than human sagacity, he yet would not deign to leave behind him any commentary or writing on such subjects; but, repudiating as sordid and ignoble the whole trade of engineering, and every sort of art that lends itself to mere use and profit, he placed his whole affection and ambition in those purer speculations where there can be no reference to the vulgar needs of life; studies, the superiority of which to all others is unquestioned, and in which the only doubt can be whether the beauty and grandeur of the subjects examined, of the precision and cogency of the methods and means of proof, most deserve our admiration. It is not possible to find in all geometry more difficult and intricate questions, or more simple and lucid explanations. Some ascribe this to his natural genius; while others think that incredible effort and toil produced these, to all appearances, easy and unlaboured results. No amount of investigation of yours would succeed in attaining the proof, and yet, once seen, you immediately believe you would have discovered it; by so smooth and so rapid a path he leads you to the conclusion required. And thus it ceases to be incredible that (as is commonly told of him) the charm of his familiar and domestic Siren made him forget his food and neglect his person, to that degree that when he was occasionally carried by absolute violence to bathe or have his body anointed, he used to trace geometrical figures in the ashes of the fire, and diagrams in the oil on his body, being in a state of entire preoccupation, and, in the truest sense, divine possession with his love and delight in science. His discoveries were numerous and admirable; but he is said to have requested his friends and relations that, when he was dead, they would place over his tomb a sphere containing a cylinder, inscribing it with the ratio which the containing solid bears to the contained. [Source: Plutarch's Marcellus, http://classics.mit.edu/Plutarch/marcellu.html , emphases supplied ]
1. If a straight line drawn in a plane revolve at a uniform rate about one extremity which remains fixed and return to the position from which it started and if, at the same time as the line revolves, a point move at a uniform rate along the straight line beginning from the extremity which remains fixed point will describe a spiral in the plane.
2. Let the extremity of the straight line which remains fixed while the straight line revolves be called the origin of the spiral.
3. And let the position of the line from which the straight line began revolve be called the initial line in the revolution.
4. Let the length which the point that moves along the straight line describes in one revolution be called the first distance, that which the same describes in the second revolution the second distance, and similarly let the distances described in further revolutions be called after the number of the particular revolution.
5. Let the area bounded by the spiral described in the first revolution and the first distance be called the first area, that bounded by the spiral described in the second revolution and the second distance the second area, and similarly for the rest in order.
6. If from the origin of the spiral any straight line be drawn, let that side of it which is in the same direction as that of the revolution be called forward, and that which is in the other direction backward.
7. Let the circle drawn with the origin as centre and the first distance as radius be called the first circle, that drawn with the same centre and twice the radius the second circle, and similarly for the succeeding circles.Although Archimedes appears to deal in generalities, there nevertheless exists in this work a hint of something else as indicated in his remarks to Dositheus, for after describing his work on spirals he introduces an additional set of propositions by remarking that: "After these came the following propositions about the spiral, which are as it were another sort of problem having nothing in common with the foregoing; and I have written out the proofs of them for you in this book" and it is here that readers are asked to remember the one-third and two-third positions on the Spiral described earlier. Thus Archimedes states next:
"ARCHIMEDES to Dositheus greeting. "Of most of the theorems which I sent to Conon, and of which you ask me from time to time to send you the proofs, the demonstrations are already before you in the books brought to you by Heracleides; and some more are also contained in that which I now send you. Do not be surprised at my taking a considerable time before publishing these proofs. This has been owing to my desire to communicate them first to persons engaged in mathematical studies and anxious to investigate them. In fact, how many theorems in geometry which have seemed at first impracticable are in time successfully worked out!...Further descriptions are supplied by Archimedes, who then states:
...... After these came the following propositions about the spiral, which are as it were another sort of problem having nothing in common with the foregoing; and I have written out the proofs of them for you in this book. They are as follows.
If a straight line of which one extremity remains fixed be made to revolve at a uniform rate in a plane until it returns to the position from which it started, and if, at the same time as the straight line revolves, a point move at a uniform rate along the straight line, starting from the fixed extremity, the point will describe a spiral in the plane.
I say then that the area bounded by the spiral and the straight line which has returned to the position from which it started is a third part of the circle described with the fixed point as centre and with radius the length traversed by the point along the straight line during the one revolution.
And, if a straight line touch the spiral at the extreme end of the spiral, and another straight line be drawn at right angles to the line which has revolved and resumed its position from the fixed extremity of it, so as to meet the tangent, I say that the straight line so drawn to meet it is equal to the circumference of the circle.
Again, if the revolving line and the point moving along it make several revolutions and return to the position from which the straight line started, I say that:
The area added by the spiral in the third revolution will be double of that added in the second, that in the fourth three times, that in the fifth four times, and generally the areas added in the later revolutions will be multiples of that added in the second revolution according to the successive numbers, while the area bounded by the spiral in the first revolution is a sixth part of that added in the second revolution.
Also, if on the spiral described in one revolution two points be taken and straight lines be drawn joining them to the fixed extremity of the revolving line, and if two circles be drawn with the fixed point as centre and radii the lines drawn to the fixed extremity of the straight line, and the shorter of the two lines be produced, I say that: (1) the area bounded by the circumference of the greater circle in the direction of (the part of) the; spiral included between the straight lines, the spiral (itself) and the produced straight line will bear to (2) the area bounded by the circumference of the lesser circle, the same (part of the) spiral and the straight line joining their extremities the ratio which (3) the radius of the lesser circle together with two thirds of the excess of the radius of the greater circle over the radius of the lesser bears to (4) the radius of the lesser circle together with one third of the said excess.
The proofs then of these theorems and others relating to the spiral are given in the present book. Prefixed to them, after the manner usual in other geometrical works, are the propositions necessary to the proofs of them. And here too, as in the books previously published, I assume the following lemma, that, If there be (two) unequal lines or (two) unequal areas, the excess by which the greater exceeds the less can, by being [continually] added to itself, be made to exceed any given magnitude among those which are comparable with [it and with] one another." [ THE WORKS OF ARCHIMEDES INCLUDING THE METHOD translated by Sir Thomas Heath, GREAT BOOKS OF THE WESTERN WORLD #11, Robert Maynard Hutchins, Editor in chief, William Benton, Chicago, 1952:248, emphases supplied]Without going into the finer details we may nevertheless take an initial cue from the information provided by Archimedes that "the area bounded by the spiral in the first revolution is a sixth part of that added in the second revolution". Simply stated, if the first area is 1 (i.e.,unity) then the second area will be 6, the third 12, the fourth 18, and so on, for according to Archimedes: "generally the areas added in the later revolutions will be multiples of that added in the second revolution according to the successive numbers", thus the areas expand by successive multiples of 6. But what does this have to do with the equiangular period spiral as derived in the previous section which concerns time and successive heliocentric revolutions? Since the revolutions in the latter also proceed according to a fixed increment, i.e., by the fundamental period constant associated with the equiangular square and the construction of the spiral itself - Phi 2- we can also obtain successive "areas" from the corresponding periods (as "radii") from the Phi-series planetary framework. And as it so happens, the "areas" pertaining to the planetary positions also expand in a uniform manner - not by 6 as given by Archimedes - but by a constant factor of 6.854101966 (Phi 4) instead, and thus 6 may (or may not) be considered a simplified approximation for the latter. But however one looks at it, the number "6" is undoubtedly of importance in Pythagorean contexts while a similar weight appears to have been placed - either directly or indirectly - on the numbers 6, 12 and 18 by Plato in the Epinomis, in theTimaeus, and elsewhere. And here we might also recall that with respect to the equiangular period spiral (with notable exceptions) that the heliocentric distances occur at the 60 and 300-degree points, thus a six-fold division is also a feature of the basic configuration. So what indeed is Archimedes referring to here? One can hardly be certain at this stage, but from what we have seen so far, one might begin to suspect that these seemingly simple operations are neither numerology nor primitive mathematics, but something quite different. It may well be that it is not common practice to treat time in radial form per se, but then again, we are not used to working with such an all-encompassing, complex entity as this particular equiangular spiral either. But if we are not dealing with numerology and elementary mathematics in this context, then what are dealing with? It may be too early to be definitive, but it is beginning to look more and more like highly condensed, competent methodology clothed in disarmingly simple terms.
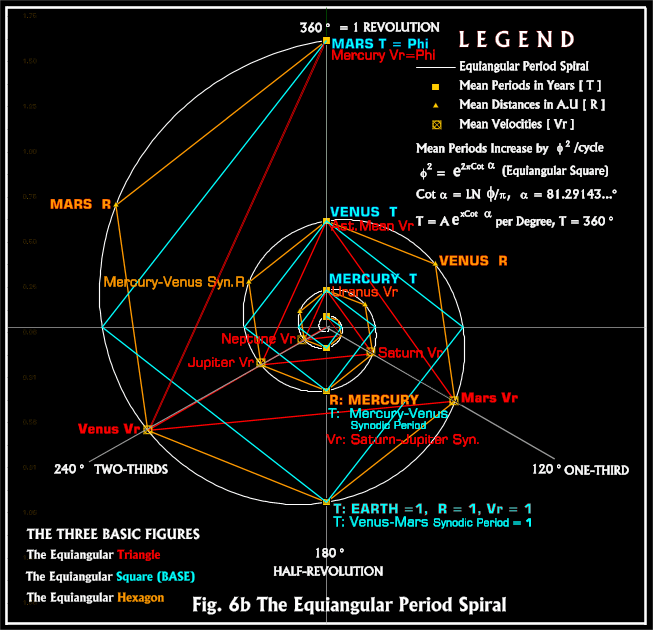
Moreover, if we recall that our final product - the equiangular period spiral, is (a) just that, i.e., equiangular, (b) that this spiral includes all three mean parameters - Periods, Distances and Velocities - and significantly (c), that the latter trio are delimited by three basic equiangular figures - the triangle, the square (more correctly the rectangle) and the hexagon - we are then able to examine Oresme's closing religious summations in Du Ciel from a more tightly focussed viewpoint:
Notwithstanding that He is everywhere, still is He absolutely indivisible and the same time infinite with respect to the three qualities that are divisible in living creatures, which we call duration, position, and power or perfection; for temporal duration of creatures is divisible in succession; their position, especially of material bodies, is divisible in extension; and their power is divisible in any degree or intensity. [Du Ciel, Book IV, Chapter 10, fols. 200a-200c, p.721]
... Besides the varieties of trinity noted there, there is another which is pertinent to our present discussion, because, in accord with what we said in chapter Twelve of Book II [see fol. 176b], there are three regular plane figures - the triangle, the square, and the hexagon - each of which we can imagine to be capable of filling so completely a flat area or surface that it is absolutely impossible that there could be more space to be filled; likewise there are three divine persons, each of whom fills all space. Isaiah the Prophet spoke of them thus: Holy, Holy, Holy, Lord God, etc. all the earth is full of thy glory. And there is one God, who spoke through His Prophet Jeremiah: I will fill the heaven and earth; and of who Virgil said: All things are replete with Jove.[Du Ciel, Book IV, Chapter 10, fols. 200d-201b, p.723]
I have recently thought of an interpretation that I should like to express here: first, with regard to a common phenomenon which we call the rainbow, and which has three colors, I assume that all these colors, and each one separately, are within the cloud where this rainbow appears and which is correctly placed to reflect them; however, to one man these colors do not appear to be throughout the entire cloud, but rather of such shape and position as a straight line coming from the center of the body of the sun and passing through the eye; this line is imagined to go straight to the center of this arc or to the circular circumference of which it is a part. It follows therefrom that two or more men not on this line cannot see this arc in the same identical place, nor can they see it as a proper arc; nevertheless, one man like the other sees it straight before his face, if he so pleases. All this I assume, without further explanation, as pure and necessary truth, demonstrated in the Meteors and in a short treatise beginning: "Among all our impressions...," etc.; all experience that we can have agrees with this assumption. Anyone could raise the doubt mentioned above if he did not understand this explanation. Therefore I ask him why Omnipotent God could not do something similar to the heavens - that is, in the supercelestial heaven, where the saved bodies would be situated in accordance with the second or third possibilities outlined in the preceding chapter [see fol. 201c] - and ask why God could not have the entire body of Christ and each of His members present throughout every part of this heaven in the same way the colors of the rainbow are situated in every part of a cloud, except that Christ's body would be everywhere the same, even according to number...[Du Ciel, Book IV, Chapter 12, fols. 202d-203a, pp.727-729]
...Therefore, we could possibly say that the body of the glorious Virgin Mary, which contained the body of Christ, is, as it were, the second rainbow and that these two glorious bodies so close to each other in nature are or will be throughout the entire heaven where the blessed bodies are and the two will fill that place just as the rainbow does, and will be seen throughout the heaven in their own proper shape, just as we said of the two perishable rainbows we can see here below. So, from this, we would have two concordant similarities: one natural, of the two arcs noted above which permeate the entire cloud; the other mathematical, in the sense that there are only two regular bodies - and there cannot be any other - which fill a place or material space: one, a pyramid or tetrahedron; and the other, a cube or hexahedron, as explained in Chapter Twelve of Book III [see fols.175d ff.]. Du Ciel, Book IV, Chapter 12, fols. 202d-203a, pp.727-729]The heavy emphasis on religious imagery notwithstanding, we must still ask just what exactly Oresme is implying here at the conclusion of what was ostensively a translation of Aristotle's De Caelo. But whether it pertains to Spira Solaris is another matter altogether, for the understanding gained in the previous Sections concerning the Phi-Series planetary framework requires both the heliocentric concept and relatively advanced mathematical skills. Thus it would be far easier to simply dismiss the above passages out of hand, especially since it is one thing to be considering the periods of revolution of the planets (e.g., the "temporal periods" in Proclus) yet quite another to suggest that either the planetary distances or the velocities were under direct consideration. After all, this would require Kepler's Third Law of planetary motion and the application of fractional exponents for the derivation of the last two parameters, i.e., an awareness of the relationships: Mean Distance R = Mean Period T 2/3 and Mean Velocity V = Mean Period T -1/3 (or initially the inverse velocity from T1/3). The determination of the last parameter could be simplified somewhat by applying the relation: V = Mean Distance R -1/2 but Du Ciel is still a fourteenth century work, and who would be able to apply fractional exponents in such contexts at this early date in any case?
Surprisingly enough, it would appear that Nicole Oresme - who already has Earth in motion - almost certainly could, for among his many endeavors was a further work on this precise subject entitled: Algorismus proportionum (Algorism of Ratios). Thus, all preconceptions aside, the necessary tools and orientation were nevertheless present. Moreover, keeping in mind that the Phi-Series planetary framework utilizes exponents of 2 and 4/3 for the increases in planetary periods and distances respectively, and the fractional exponents: 2/3, 1/3 and ½ are those specifically applied in the above astronomical context, it may not be entirely coincidental that Part I of Oresme's Algorism of Ratios commences with:
One half is written as ½, one third as 1/3, and two thirds as 2/3, and so on. The number above the crossbar is called the numerator, that below the crossbar the denominator. A double ratio [ i.e., 2/1 ] is written 2 p, a triple ratio [ i.e., 3/1 ] as 3 p, and so forth. A sequialterate ratio [ i.e., 3/2 ] is written as 1 p ½, and a sequitertian ratio [ i.e., 4/3 ] as 1 p 1/3. A superpartient two-thirds ratio [ 5/3 ] is written a 1 p 2/3, a double superpartient three-fourths [ i.e., 11/4 ] as 2 p 3/4, and so on. Half a double ratio [i.e., (2/1) ½ is written as ½ 2 p and a fourth part of a double sesquialterate [ i.e., (5/2) 1/4 ] as 1/4 2 p ½, and so on. But some times a rational ratio is written in its least terms or numbers just as a ratio of 13 to 9, which is called a superpartient four-ninths [ i.e., 1 4/9 ]. Similarly, an irrational ratio such as half a superpartient two-thirds [ i.e., (5/3) ½ ] is written as half of a ratio of 5 to 3.One could say that it would be both natural and beneficial to employ fractional exponents involving the first few integers in such a discourse, as well it might. But even so, useful information is undoubtedly provided here that simplifies calculations directly applicable in astronomical contexts, e.g., Oresme tackles 42/3 by the simple expedient of converting 42/3 to (42)1/3 = 161/3 thus reducing 42/3 to obtaining the cube root of 16.[Grant: 1965:331] More complex rules and operations follow, including the subtraction of a "sesquitertian" ratio of 4/3 from a "sesquialterate" one of 3/2 to produce an exponential ratio of 9/8, of which Oresme states: "A sesquialterate ratio is, therefore, greater that a sesquitertian ration by a ratio of 9 to 8, that is, greater by a sesquioctavan ratio. This can be shown by the twenty-seventh proposition of the second book of the Arithmetic of Jordanus."[Grant: 1965:331]. Here, and as one reads further, many of the succeeding numbers, ratios and terms used by Oresme are familiar, i.e., they are more often than not members of Plato's "Double" and Triple" intervals ( [ 1, 2, 4, 8 ] and [ 1, 3, 9, 27 ] respectively ) and/or related values discussed in Plato's Timeus and elsewhere in the Dialogues. For example, Oresme states in Du Ciel, Book IV, Chapter 7, fols.193d-194a:
Every irrational ratio - and these shall now be considered - is denominated by a rational ratio in such a manner that it is said to be a part or parts of the rational ratio, as [for example] half of a double [i.e., (2/1) 1/2], a third part of a quadruple [i.e., (4/1)1/3, or two thirds of a quadruple [ i.e., (4/1) 2/3 ]. [Edward Grant, Part I of Nicole Oresme's Algorismus proportionum, ISIS, Vol 56, 3, No.185, 1965:328-9]
Between the contrary colors black and white, there are many intermediate colors. Also, between the regions of fire and earth there is an intermediate region which cannot be empty and in which there must be at least one body or two; it cannot be a simple body because fire, which is hot and dry, must have a simple body of the opposite nature or water, which is cold and moist. Likewise, the earth must have contrary body, and this is air. So, with respect to place, air and water are intermediate bodies between the fire and earth. But Plato proves this conclusion by pointing out that between the cubes of two numbers there must necessarily be two other mean [proportional] numbers, bearing not a greater or lesser but the same proportion to each other as that between the number originally cubed; as, for example, between the first cubic numbers 8 and 27 there are the means [proportionals] 12 and 18, having to each other a continuous sesquialterate proportion [ of 2 : 3 - which were the original numbers to be cubed ]. In Plato's opinion, this explains the existence of two elements, air and water, between the fire and earth. [Menut,1968:701, emphases supplied]Here we find a clear allusion to numerical and technical details used in the construction of the "World Soul" in the Timeus linked with colours, bodies, qualities and the four primary "elements" - Fire, Air, Water and Earth, etc. Thus we are now drawn into considering both alchemical and pythagorean terms, and neither subject is necessarily as straightforward or as simple as prevailing wisdoms would have it; in fact with respect to the latter the unwary might find it beneficial to dwell on the following admonition:
"De Pythagoreis sine lumine, ne loquitor" (Do not criticize the Pythagoreans without light) or, a little more bluntly:
"Do not criticize the doctrines of the Pythagoreans unless you understand them..."
Since it appears that Nicole Oresme may have been discussing relatively advanced concepts - the laws of planetary motion included - it becomes necessary to track down the source and fount of his apparent wisdom. And here the unlikely use of the Third Law of Planetary Motion itself provides us with an indication. Although against conventional understanding, it is nevertheless possible to suggest that it is far from certain that the laws of planetary motion were entirely unknown before Kepler's time. In this regard, Oresme's remarks concerning the insights provided by the Arab scholar Ibn Rushd (Averroes) are significant since Ibn Rushd - who flourished from 1128 to 1198 CE - was renowned for his erudition in general and his Commentaries on the works of Aristotle and Plato in particular, including the latter's Republic. Thus Oresme records in Du Ciel that:
"In Book Twelve of the Metaphysics, Averroes states that the regularity of the celestial system is of the same sort as the government of a city, with a prince who acts as sovereign and the other officers each following in obedience to him. Averroes makes another analogy comparing the order of the heavens with several crafts all of which serve under the principal one. In the same way, the intelligences cause the movements of the heavens under the sovereign intelligence which causes the daily movement. It follows then, that just as the offices and leaders of the city differ in species, exactly like the different members of a body; and Averroes states that the heavens are a living body." [ Book II, Chapter 16, fols. 121c-121d., p.465; emphases supplied ].The above is notable for two things in particular, the notion that the Heavens (better perhaps, the Solar System) corresponds to a living entity, and the use of "political" analogies in the same context, which surely supplies both meaning and understanding to the well-known, but puzzling passage in Plato's Republic concerning the number of the Tyrant, especially if we keep in mind Plato's Triple Interval [ 1, 3, 9, 27 ] and the relation: 93 = 272 = 729 applied to a mean distance of 9 (reference to unity) and the corresponding mean period of revolution of 27 years:
Hence, if I am not mistaken, the tyrant will be furthest from, and the king nearest to, true and specially appropriate pleasure. It is undeniable. And therefore the tyrant will live most unpleasantly, and the king most pleasantly. It is quite undeniable. And pray are you aware of the extent to which the discomfort of the tyrant's life exceeds that of the king's. I wait for you to tell me. There are three pleasures, it appears,- one genuine, and two spurious. Now the tyrant has trespassed beyond these last, has fled from law and reason, and lives with a bodyguard of slavish pleasures: The extent of his inferiority is hard indeed to state, unless perhaps it may be stated thus. How? Reckoning from the oligarchical man, the tyrant stands third, I believe, in the descending line: for the democratical man stood between. Yes. Then, if our former remarks were true, must not the pleasure with which he consorts, be, so far as truth is concerned, a copy of a copy, the original of which is in the possession of the oligarchical man? Just so. And again, reckoning from the kingly man, the oligarchical in his turn stands third in the descending line, supposing us to identify the aristocratical and the kingly? To be sure, he does. Therefore the tyrant is thrice three times removed from true pleasure. Apparently so. Then it seems that tyrannical pleasure may be represented geometrically by a square number, 9. Exactly so. And by squaring and cubing, it is made quite clear to what a great distance the tyrant is removed. Yes, to an arithmetician it is. Conversely, if you wish to state the distance at which the king stands from the tyrant in point of reality of pleasure, by working out the multiplication you will find that the former lives 729 times more pleasantly that the latter, or that the latter lives more painfully than the former in the same proportion. You have bought out an extraordinary result in calculating the difference between the just man and the unjust, on the score of pleasure and pain. Well, I replied, I am sure that the number is correct, and applicable to human life, if days and nights and months and years are applicable thereto. And no doubt they are. [ Republic, IX, 587b-588a, trans. John Llewellyn Davies, emphases supplied]In addition to above with its clear references to "distance," "9", 27 ( "thrice three times" ), "squaring and cubing," the number "729" and not least of all time, there are further mathematical sequences associated with "political" structures and the organization of labour in Plato's Republic and elsewhere that have long attracted the interest and attention of scholars. Moreover, investigating further we find among pythagorean fragments additional information, e.g.,.
22. C. ... Law is useful to the political society if it is not monarchial, if it does not constitute privileged classes, if it is made in the interest of all, and is equally imposed on all. Law must also regard the country and the lands, for not all soils can yield the same returns, neither all human souls the same virtues. That is why some establish the aristocratic constitution, while other prefer the democratic or oligarchic. The aristocratic constitution is founded on the sub-contrary proportion [ Harmonic Mean ], and is the most just, for this proportion. in which the results of the great and small are equal [ in ratio ]. The oligarchic and tyrannic constitutions are founded on the arithmetical proportion, which, being the opposite of the subcontrary, attributes to the smallest terms the greatest results, and vice versa. [emphases supplied]
16 Explaining himself about the means, Archytas writes: In music there are three means: the first is the arithmetical mean, the second is the geometrical, the third is the subcontrary mean, which is called harmonic. The mean is arithmetical, when three terms are in a relation of analogical excess, that is to say, when the difference between the first and the second is the same as the difference between the send and third; this in proportion, the relation of the greater term is smaller, and the relation of the smaller is greater. The geometric mean exists when the first term is to the second as the second is to the third; here the relation of the greater is identical with the relation of the smaller terms. The subcontrary mean, which we call harmonic, exists when the first term exceeds the second by a fraction of itself, identically with the fraction [of the third] by which the second exceeds the third; in this proportion the relation of the greater terms is greater, and that of the smaller, smaller." [ emphases supplied, [p.185]This is the same Archytas mentioned in the previous Section, i.e.,
The first who methodically applied the principles of mathematics to mechanics; who imparted an organic motion to a geometric figure, by the section of the semi-cylinder seeking two means that would be proportional, in order to double the cube. [emphases supplied]Thus remaining with the "subcontrary mean" described above, taking any three successive periods of the phi-series planetary framework - for example, for Saturn, the intervening synodic cycle and that of Jupiter for the first, second and third terms respectively - we obtain:
| TERM | POSITION | PERIOD: T | Difference: D | FRACTION:T/D |
| FIRST | SATURN | 29.03444185 | - | - |
| SECOND | Synodic | 17.94427190 | 11.09016994 | 0.381966011 |
| THIRD | JUPITER | 11.09016994 | 6.854101969 | 0.381966011 |
| Relation: Greater to Smaller: 11.09016994 to 6.854101969 | ||||
C. THE DOUBLE AND TRIPLES INTERVALS AND THE LAWS OF PLANETARY MOTION
[ 1a ] MEAN PERIOD (T) 2 = MEAN DISTANCE (R) 3 = MEAN VELOCITY (V) - 6
[ 1b ] T 2 = R 3 = V - 6
e.g., for mean periods of revolution of T
= 8 , T = 27 and T = 1000
years respectively,
for the Double :[ 1,
2, 4, 8 ], Triple [ 1, 3,
9, 27 ] and Decadic interval [ 1,
10, 100, 1000 ]:
4 3 = 8 2 = 64 = 2 6 or (2 2 ) 3 = (2 3 ) 2 = 2 6
9 3 = 27 2 = 729 = 3 6 or (3 2 ) 3 = (3 3 ) 2 = 3 6
100 3 = 1,000 2 = 1,000,000 = 10 6 or (10 2 ) 3 = (10 3 ) 2 = 10 6
T = R/V
R = VT
V = R/T
| VELOCITY:V | DISTANCE:R | PERIOD:T | V = R/T | R = VT | T = R/V | UNITY | Vi | R | T | INTERVAL |
| 0.5 | 4 | 8 | 0.5 | 4 | 8 | 1 | 2 | 4 | 8 | DOUBLE |
| 0.33333333 | 9 | 27 | 0.3333333 | 9 | 27 | 1 | 3 | 9 | 27 | TRIPLE |
| 0.11111111 | 100 | 1000 | 0.1111111 | 100 | 1000 | 1 | 10 | 100 | 1000 | DECADIC |
Table 1. The Double,
Triple and
Decadic Intervals
in Astronomical context.
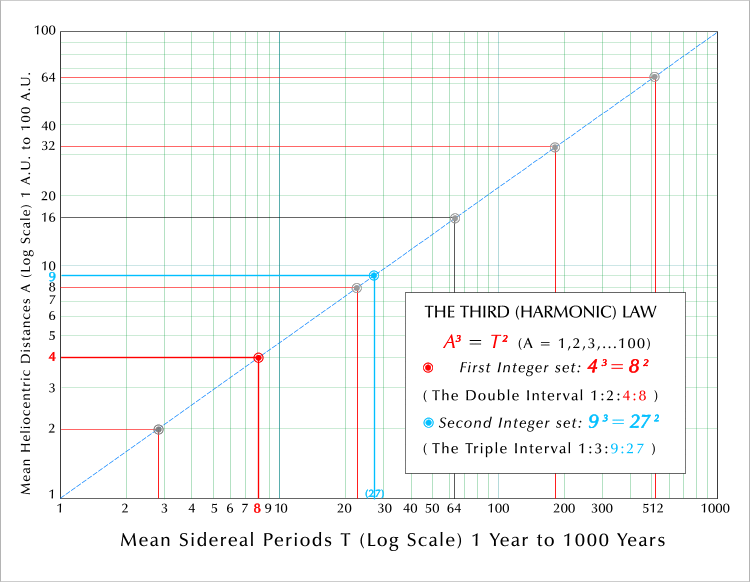
Fig. 6c. The Double and Triples Intervals, the Harmonic Law, and the Solar System.
Returning to the political allusions provided by Ibn Rushd and Plato's Republic, we find that there is an ever-widening range of symbols and meanings to be considered, including "metals" ,"marriage" and "offspring" in only slightly disguised alchemical contexts. Moreover, we also find in the Republic an explanation of the methodology, which is clearly stated as a dubious tale, if not indeed a subterfuge:
While all of you in the city are brothers, we will say in our tale, yet God in fashioning those of you who are fitted to hold rule mingled gold in their generation, for which reason they are the most precious - but in the helpers silver, and iron and brass in the farmers and other craftsmen. And as you are all akin, though for the most part you will breed after your kinds, it may sometimes happen that a golden father would beget a silver son and that a golden offspring would come from a silver sire and there would in like manner be born of one another. So that the first and chief injunction that the god lays upon the rulers is that nothing else are they to be such careful guardians and so intently observant as of the intermixing of these metals in the souls of their offspring, and if sons are born to them with an infusion of brass or iron they shall by no means give way to pity in their treatment of them, but shall assign to each the status due to his nature and thrust them out among the artisans or the farmers. And again, if from these there are born sons with unexpected gold or silver in their composition they shall honour such and bid them go up higher, some to the office of guardian, some to the assistantship. alleging that there is an oracle that the state shall be overthrown when the man of iron or brass is its guardian. Do you see any way of getting them to believe this tale? No, not of these themselves, he said, but I do their sons and successors and the rest of mankind who come after. [Republic III, 414d-415c. Trans. Paul Shorey, emphases supplied]Further clarification regarding the above passage is provided in Robert S. Brumbaugh's Plato's Mathematical Imagination, i.e., Brumbaugh observes: "The explicit mention of all the other combinations after the examples given suggests that behind this story lies some scientific explanation of the genetic phenomenon, which would be based on a combination diagram of the possible kinds of parental ability."
| PLANETS Synodics |
N | METAL | PERIOD: T | DISTANCE: R | VELOCITY: V |
| Phi n | - | Phi n=T=R/V | R = VT | V = R/T | |
| MERCURY | -3 | SILVER | 0.2360679 | 0.38196601 | 1.6180339 |
| Synodic | -2 | - | 0.38196601 | 0.52644113 | 1.37824077 |
| VENUS | -1 | BRASS | 0.61803399 | 0.72556263 | 1.17398500 |
| EARTH/Syn | 0 | - | 1 | 1 | 1 |
| MARS | 1 | IRON | 1.6180339 | 1.3782408 | 0.8517996 |
| Synodic | 2 | - | 2.6180340 | 1.8995476 | 0.7255626 |
| Asteroid Belt | 3 | - | 4.2360680 | 2.6180340 | 0.6180339 |
| Synodic | 4 | - | 6.8541020 | 3.6082812 | 0.5264411 |
| JUPITER | 5 | TIN | 11.0901699 | 4.9730803 | 0.4484224 |
| Synodic | 6 | Antimony | 17.9442719 | 6.8541020 | 0.38196601 |
| SATURN | 7 | LEAD | 29.0344419 | 9.4466028 | 0.3253585 |
| (Synodic) | 8 | - | 46.9787138 | 13.0196931 | 0.2771403 |
| URANUS | 9 | - | 76.0131556 | 17.9442719 | 0.2360679 |
Table 2. Metals and the Phi-Series
Planetary
Framework
(Mercury-Uranus).
As we have already noted in Section Three, the elliptical nature of the planetary orbits cause the actual synodic periods to vary; in the case under consideration the synodic periods of Mars with respect to Jupiter at times actually intercept the Earth-Mars synodic difference cycle and further complications arise if the other inferior planets are also factored into the equation. However, remaining with mean values based on modern estimates for the periods of Mars and Jupiter (1.880711 and 11.856252 years respectively) the mean synodic period that corresponds to "Antimony 2" (see Table 3 below) is 2.2352856 years, which may (or may not) be compared directly with that obtained from the ratio: 239/106 = 2.2547169 (years) - " the proportion of Iron to antimony " enumerated in the third chapter of the Aesch-Mezareph - a Cabalistic work that also links with the "Iron" and "opening of the mouth" of ancient Egypt (i.e., The Egyptian Book of the Dead, and West 1993:83; see also Aristotle, Metaphysics, Book XIV, Part 6 for the Pleiades and the Bear concerning the numbers 7 and 12):
Barzel, Iron; in the Natural Science, this Metal is the middle Line, reaching from one extreme to the other. This is that Male and Bridegroom, without whom the Virgin is not impregnated. This is that Sol, Sun or Gold of the Wise Men, without whom, the Moon will be always in Darkness. He that knows his Rays, works in the Day; others grope in the Night.In remains now to assign the name "Soul" to the mean periods (T), the name "Body" to the mean distances (R) and "Spirit" to the mean velocities (V) as shown in Table 3. The obscure terminology and multiplicity of meanings that pervade "Alchemy" notwithstanding, casual readers and disbelievers alike may nevertheless now find the following cryptic remarks in a relatively modern commentary on this esoteric subject at least partially understandable:
Parzala, whose lesser number is 12, is of the same account as the Name of that Bloody animal Dob, a Bear, Whose Number is 12 also.
And this is that Mystical thing, which is written, Dan., 7, 5, "And behold another Beast, a second like unto a Bear, stood on its one side, and it had three Ribs standing out in his Mouth, between his Teeth; and thus they said unto it, Arise, eat much Flesh." The Meaning is, that in order to constitute the Metallic Kingdom, in the second place, Iron is to be taken; in whose Mouth or Opening (which comes to pass in an Earthen Vessel) a threefold Scoria is thrust out, from within its whitish Nature. Let him eat Batsar, i.e., Flesh, whose lesser Number is 7, that is Puk, that is Stibium, whose lesser Number in like manner is 7. And indeed much Flesh, because the proportion of this, is greater than of that; and indeed such a proportion as Puk, that is 106, bears to Barzel 239; such shall be the proportion of Iron to Antimony. [Aesch-Mezareph, Ch. 3, in [Collectanea Hermetica, edited by William Wynn Westcott, Kessinger books, Kila [ISBN 1-56459-260-X, pp.23-24. emphases supplied]
| PLANETS Synodics | N | METAL | PERIOD: T | DISTANCE: R | VELOCITY: V |
| Phi n | - | Phi n=T=R/V | R = VT | V = R/T | |
| MERCURY | -3 | SILVER | 0.2360679 | 0.38196601 | 1.6180339 |
| Synodic | -2 | - | 0.38196601 | 0.52644113 | 1.37824077 |
| VENUS | -1 | BRASS | 0.61803399 | 0.72556263 | 1.17398500 |
| Synodic | 1 | - | 1.6180339 | 1.3782408 | 0.8517996 |
| EARTH | 0 | - | 1 | 1 | 1 |
| Synodic | 2 | - | 2.6180340 | 1.8995476 | 0.7255626 |
| MARS | 1 | IRON | 1.6180339 | 1.3782408 | 0.8517996 |
| Synodic | "4/3" | Antimony2 | 1.89442711 | 1.53103556 | 0.8081786 |
| JUPITER | 5 | (TIN) | 11.0901699 | 4.9730803 | 0.4484224 |
| Synodic | 6 | Antimony1 | 17.9442719 | 6.8541020 | 0.38196601 |
| SATURN | 7 | (LEAD) | 29.0344419 | 9.4466028 | 0.3253585 |
| (Synodic) | 8 | - | 46.9787138 | 13.0196931 | 0.2771403 |
| URANUS | 9 | - | 76.0131556 | 17.9442719 | 0.2360679 |
| NAME | - | - | "SOUL" = T | "BODY"= R | "SPIRIT"= V |
Table 3. Metals and the Phi-Series Modified Planetary Framework (Mercury - Uranus).
There is indeed another antimony, which is our sulphur, and the subject of the whole art; but this is so hard to find, and when it is found, so hard to prepare, that it had almost cast me into despair. How- soever if thou dost seriously consider what I have written, and what hath fallen from me in some places with as much purpose as caution, then verily neither the thing itself not the preparation of it can be hid from thee. To make an end, know that the philosophers have two mercuries or waters, the first and second, their first is the spirit of our antimony and here understand me rightly; their second is that of mercury and Venus philosophical, and this of itself is all sufficient; but to shorten time, the philosophers ferment it with common gold. [Collectanea Hermetica, edited by William Wynn Westcott, Kessinger books, Kila [ISBN 1-56459-260-X, p. 91. emphases supplied]The preceding discussions concerning common alchemical/numerical elements in diverse works such as Plato's Republic, a relatively modern alchemical work, and a variant with ancient origins inThe Aesch-Mezareh suggest that the underlying framework is more complex and widespread than previously suspected. In this present Section we have necessarily shifted from The Middle Ages and the insights of Ibn Rushd to touch lightly on much earlier works by Aristotle, Plato and Pythagoras. In doing so, however, we have been obliged to proceed from arabic texts translated into Latin on through medieval French to the English language version of Oresme's Le livre du ciel et du monde. In light of the understanding provided by Ibn Rushd it now seems likely that the best sources for further research would be the extant Arabic writings themselves along with their perceptive commentaries and expositions. As it stands at present, it seems unavoidable that we (in the West at least) encounter what are essentially commentaries on commentaries, multiple translations, and perhaps even the agendas of special interest groups along the way. To which may also be added that even with the best of intentions, scholarship without context, and commentary without understanding may still have created eminently readable, yet relatively meaningless renditions of ancient wisdom. Moreover, there is still the question of origins to be considered and further complexities associated with "Alchemy" to be addressed. Nor is the latter as simple as it might seem, either in earlier or more modern contexts, for it is abundantly clear that alchemy almost certainly does not concern the actual transmutation of base metals into gold. In fact, as discussed in some detail in later Sections and in a very limited fashion above, this subject appears to have far more to do with the complexities of the Golden Section in our current astronomical context than anything else. Nor do matters get any simpler when it is realized we have not yet discussed colours, quantities, qualities, harmony, the four elements, the two triangles, the five solids, or the detailed technical formation of the "World Soul" described in Plato's Timeus. Moreover, we have yet to understand what was meant by "Form, Matter, and the Perceptible" and related topics such as "The Diagonal of the Diagonal" (Statesman, 266a-267c) or "The First of Unities" (Plutarch, De Anim. Procreat.) etc. In terms of such difficulties, it might well be that Giorgio de Santillana and Hertha von Dechend were essentially correct when they concluded at the end of Hamlet's Mill (Gambit, Boston, 1969:348) that:
there is nothing left of the ancient knowledge except relics, fragments and allusions that have survived the steep attrition of the ages. Part of the lost treasure may be recovered through archaeology; some of it - Mayan astronomy, for instance - may be reconstructed through sheer mathematical ingenuity; but the system as a whole may lie beyond all conjecture, because the creating, ordering minds that made it have vanished forever.However, in our present situation we have a detailed mathematical framework that provides the basis for the next phase, duly augmented by guidance from Hermes Trimegistos. Nevertheless, we will not only have to "separate Earth from Fire," as the latter instructs, but also "separate Water from Earth" before we are able to appreciate the related complexity of Plato's Doctrine of the Timeus in our present context.
REFERENCES AND RELATED WORKS
Brumbaugh, R.S. Plato's
Mathematical Imagination,
Indiana University Press, Bloomington, 1977: 284.
Burges, G. The Works of Plato, Vol VI. (Incl.
Timeus the Locrian) George Bell & Sons, London, 1876.
Chadwick, H. Boethius: The Consolation of Music,
Logic, Theology and Philosophy, Clarendon Press, Oxford, 1981.
Cornford, F. M. Plato's Cosmology The Timeus of
Plato, Bobbs-Merrill, Indianapolis, 1975.
____________ Plato's Theory of Knowledg,
Routledge & Kega Paul, London, 1934.
Crosby, H. L. Thomas Bradwardine. His Tractus
de Proportionibus. Its significance for the development of Mathematical
Physics (University of Wisconsin Press, Madison 1955.
Drake, S. "Medieval ratio theory vs compound medicines
in the origins of Bradwardine's rule,"ISIS Vol. 64 No. 221,
1973:
67-77.
Davies, J. L. and D. J. Vaughan, The Works of
Plato, Vol. II, The Republic, The Nottingham Society, New York.
_____________ "Bradwardine's function, mediate denomination,
and multiple continua," Physis - Riv. Internaz. Storia Sci. 12 (1)
1970:
51-68.
Dobbs, B.J.T. The Foundations of Newton's Alchemy
or: The Hunting of the Green Lion, Cambridge University Press,
Cambridge
1975.
Dolnikowski, E.W, Thomas Bradwardine : a view
of time and a vision of eternity in fourteenth- century thought,
Leiden
1995.
Grant, E. "Part I of Nicole Oresme's Algorismus proportionum," ISIS,
Vol. 56, 3, No. 185, 1965:327-341.
____________ Nicole Oresme and the Kinematics
of Circular Motion,, University of Wisconsin Press, Madison 1971.
____________ De proporitionibus proportinum and
Ad pauca respicientes, University of Wisconsin Press, Madison 1966.
Guthrie, K. S. The Pythagorean Source Book and
Library, Phane Press, Grand Rapids 1988.
____________ The Neoplatonic Writings of Numenius,
Selene Books, Lawrence 1987.
Heath, Sir Thomas, Trans. The Works of Archimedes
Including the Method, Great Books of the Western World #11, Robert
Maynard Hutchins, Editor in chief, William Benton, Chicago, 1952.
Huntley, H. E. THE DIVINE PROPORTION, Dover
Publications, New York 1970.
Kappraff, J. CONNECTIONS: The Geometric Bridge
between Art and Scienc, McGraw-Hill, New York 1991.
Laird, A. G Plato's Geometrical Number and the
Comment of Proclus (Monograph) George Banta Publishing Company,
Menasha 1918.
Menut, Albert D. and Alexander J. Denomy, Le Livre
du ciel et du monde, University of Wisconsin Press, Madison 1968.
Santillana, G and H. von Dechend, Hamlet's Mill:
An Essay on Myth and the Frame of Time, Gambit Books, Boston,
1969:349.
Stanley, T. The Chaldean Oracles as Set Down by
Julianus, Heptangle Books, Gillette 1939.
Takahashi, K. " The mathematical foundations of Bradwardine's
rule," Historia Sci. 26, 1984:19-38.
Taylor, T. The Commentaries of Proclus on the
Timeus of Plato, (Five Books in Two Volumes) Kessinger Books, Kila
[ISBN 1-56459-349-5].
____________ PLATO: The TIMAEUS and THE CRITIAS,
Thomas Taylor Translation, Bollingen Series, Pantheon Books, Washington
1944.
____________ THE REPUBLIC, Kessinger Books,
Kila [ISBN 1-56459-024-0].
Wells, D. The Penguin Dictionary of Curious and
Interesting Numbers, Clays Ltd, St. Ives 1987:67.
West, John. A. Serpent in the Sky:The High wisdom
of ancient Egypt, Quest Books, Wheaton 1993:83.
Westcott, W. W (Ed.) Collectanea Hermetica,
Kessinger books, Kila [ISBN 1-56459-260-X].
Valens, E. G. THE NUMBER OF THINGS, Methuen
& Company, London 1965.
(Ovid) quoted by Nicole Oresme in Du Ciel,
Book II, Chapter 25, fols. 144a-144b, p.537.
Copyright © 1997. John N. Harris, M.A.(CMNS). Last Updated on March 31, 2009.