Lux et Tenebris
APPENDIX TO THE PHEIDIAN PLANORBIDAE
THE MATTER OF LOST LIGHT

As Sir Theodore Andrea Cook pointed out long ago (1914:414), there are any number of equiangular spirals that lie between the limits set by a straight line and a circle. Which may or may not provide a partial explanation for the present lack of progress in coming to terms with the many spiral configurations so clearly evident in shells. This state of affairs is especially surprising when the universal availability of the modern computer is taken into consideration, but perhaps this is also part of the problem, i.e., a general lack of focus allied to the use of the computer as a toy rather than scientific tool. In fact forty years have passed since David Raup48 first introduced computer simulation of shells, but little in the way of qualification or quantification appears to have followed thereafter. Instead, the subject appears to have been spread so wide of late that it is in grave danger of dissipating entirely rather than being consolidated and refined further. Which again is puzzling given the start obtained in 1962, as Tony Phillips recounts 49 in "The Mathematical Study of Mollusk Shells"

The paleontologist David Raup, then at Cornell, published a paper in 1962 (Science 138:150-152) entitled "Computer as aid in describing form in gastropod shells." He showed how a computer could be programmed to make images of the equiangular spiral model with several parameters. To put this achievement in perspective: the term "computer graphics" was coined around 1960, and Spacewar, the first video game ever, was designed in 1961. What is even more remarkable is that a video sampling of Raup's models (which were made by tailoring waveforms on an oscilloscope screen) is still on display in the Mollusk galleries of the American Museum of Natural History in New York. My chancing on that exhibit was the impetus for this column.
    The video is part of an installation called "Spirals and Shell Variation" which also includes wire models and a variety of specimens. In the video, entitled "The Geometry of the Coiled Shell," Raup gives a bare-bones presentation of the potential of his method. Only three parameters are illustrated: rate of aperture expansion, rate of departure from axis, and rate of descent along axis; the parameter values are described ("0," "small," "large") qualitatively.  Seven different natural morphologies are simulated (Nautilus, Spirula, Valvata, Goniobasis, Vermicularia, Anadonta (a bivalve) and Bulla) with in most cases a specimen for comparison.

Nor can it be said that considerable strides had not already been made years ago by the likes of Canon Mosely (1838) and his contemporaries, or that the continuance of the latter's treatment by Sir D'Arcy Wentworth Thompson was not widely available (at least in the complete and unabridged edition of On Grow and Form published in 1917, 1942 and 1992)50. Take, for example, the Nautilus, the first shell mentioned in the above quotation, most likely the same Nautilus that Sir D'Arcy Wentworth Thompson declined to discus in detail because he preferred instead (along with Mosely) to deal with the more complex turbinated shell Turritella duplicata 51.
   For my own part I must admit that prior to April of this year (2002) that I had not addressed the spiral formation in shells at all, and moreover, I came across Sir D'Arcy Wentworth's seminal On Growth and Form and the contributions of Canon Mosely rather late in my inquiry. Partly, no doubt because of my less than perfect methodology, but also partly because although the latter pair provide by far the best starting point for spiral forms in shells, no clear signposts to this effect were available to point the way. Not only this, but two quite different versions of the latter work exist, one with a sizeable amount of material pertaining to shells and the entire chapter on phyllotaxis expunged in an abridged edition first published a year before the Raup paper in 1961 and reprinted thereafter in 1969, 1971, 1975, 1977, 1981, 1983, 1984, 1988, 1990, 1992, 1994, 1995, 1997and 2000. Here even the cross-section of the Nautilus shown on the front page is degraded, though ultimately it is still identifiable as k = Phi 7/3.
   But in any case, my own analyses proceeded from ammonites (by way of Simon Winchester's introduction to the subject as noted above) to ramshorn snails, seashells and the associated works of Sir Theodore Andrea Cook (The Curves of Life, 1914), Samuel Colman (Nature's Harmonic Unity, 1911) and then finally to the details in Thompson's On Growth and Form (1917,1942). Because of this circuitous route I found that by initially concentrating on two-dimensional growth factors that I had perhaps naturally emulated Mosely's "characteristic" numbers. In the interim I had also been working my way through various shells (some easy, some difficult and some still unassigned) before finally coming across the latter's analyses laid out in great detail by Sir D'Arcy Wentworth Thompson. Having followed my own route, however, the "characteristic" numbers discussed by the latter were by this time hardly new, in fact for the most part they were immediately recognizable as two or four-decimal place pheidian growth factors--specifically  Phi 1/3, Phi 7/6and Phi 1/4--the latter pair being rarer in my own limited experience, with k =  Phi 7/6 (growth factor: 1.753149344) given by Mosely to two decimal places as 1.75.
   All this, mind you, by 1838, while the Raup approach still apparently provides little or no integration or semblance of order. Indeed, during the ammonite phase of testing it so happened that one of the ammonites examined was Euhopites truncatus Spath 1925 from the collection of the late Jim Craig,52 which coincidentally was also discussed in the above paper. The results of the respective assignments for this example are shown below with Spira Solaris positioned firstly with respect to the inner visible spiral, secondly with respect to the outline [ I ], and next [ II ] superimposed on the somewhat angular spiral generated by the Raup approach, the latter thus also essentially Spira Solaris.

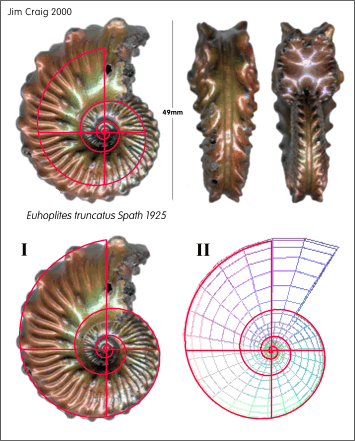Fig. 21. Ammonite Euhoplites truncatus Spath 1925

Fig. 22. Ammonite Euhoplites truncatus Spath 1925 and the single spiral k = Phi 2

The difference, being of course, that there are no trial and error operations attending Spiral Solaris, or indeed any of the Pheidian planorbidae. Moreover, there is a great deal that can be accomplished before the introduction of the third dimension, which has perhaps been part of the problem in recent times, namely a general lack of focus coupled with a dearth of choices. Too inviting a diversion, and also too distracting, it would seem. 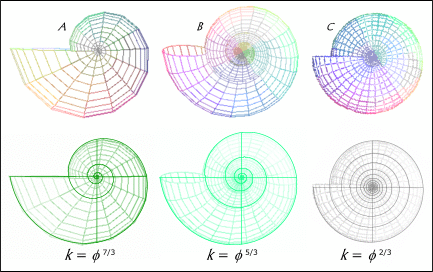Other matches from the above paper include a side view fit for Nautilus pompilus (as before, k = Phi 7/3); the ammonite Astroceras obtusum ( k = Phi 5/3), Bellerophina minuta ( k = Phi 2/3):
Methodologies and Single Spirals
Fig. 22a. The single spirals k = Phi 7/3, k = Phi 5/3  and k = Phi 2/3

plus bi-valve Mya arenia (a rare side view: k = Phi 10). It should be noted here that mathematical details are certainly presented in abundance the above paper, but perhaps in too much multi-dimensional detail to provide order and connectivity, at least in pheidian terms.

  This appears to be a prevailing problem at present, for computer generated profusion and dispersion also occurs in science popularist Richard Dawkins'  "Museum of All Shells" (Climbing Mount Improbable, 1996).53 Then again, it is difficult to know what to make of a book that although dealing with natural growth does not even mention the Fibonacci Series in the Index. 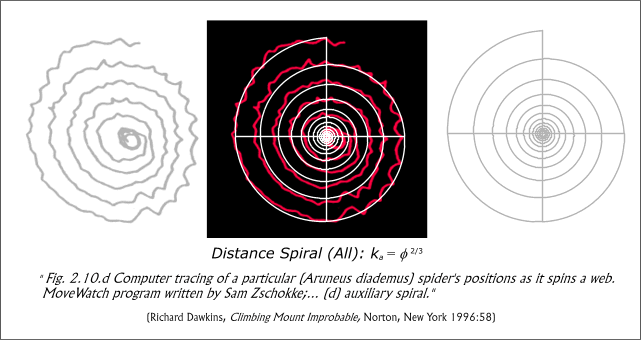Nor do some of the  more sophisticated methods involving the use of computers in this book appear to have been well maximized either, e.g., Fig. 2.10.d ("Computer tracing of a particular spider's positions as it spins a web. MoveWatch program written by Sam Zschokke.") records an auxiliary spiral constructed by the spider Aruneus diademus,54 which though somewhat irregular nevertheless provides a ready fit for the pheidian spiral k = Phi 2/3.

Fig. 22b. Web of Aruneus diademus and the single spiral k = Phi to the two-thirds power
Fig. 22b. Web of Aruneus diademus and the single spiral k = Phi 2/3

But there is more to the engineering prowess of the spider in any case, not least of all its outer commencement point and inward motion during web construction--logical enough and necessary perhaps, but the implications remain profound.

   And so, sadly, are the implications of the apparent decline in understanding that appears to have followed successful investigations into the spiral formation in nature carried out over the last three centuries. Particularly in the case of shells, it would seem, but it was not the general treatment of this subject in Sir D'Arcy Wentworth Thompson's voluminous On Growth and Form that served to emphasize the decline, but Canon Mosely's convoluted treatment of the shell Turbo duplicata in 1838. Indeed, one glance at the data and the means of presentation was enough to elicit both surprise and great admiration--as D'Arcy Wentworth Thompson duly noted in On Growth and Form--"Canon Mosely was a man of great and versatile ability" 55and here was at least partly why.

   But for myself it was something else in addition. In pursuing the line of inquiry followed by Galileo in a 1989 paper entitled: " Projectiles, Parabolas, and Velocity Expansions of the Laws of Planetary Motion" (Journal of the Royal Astronomical Society of Canada; RASC, Vol 83, No. 3,1989:207-218) I had long been puzzled by the obvious fact that if I could deduce what Galileo had laid out in the New Sciences (he had, after all, left sufficient clues) then others should surely have been able to do the same. Now it would appear that some indeed had, and well before my time in addition, including both Canon Moseley (1838) and Sir D'Arcy Wentworth Thompson (1917). Nor does there seem to be much doubt about this either; it is quite clear what Mosely delivered with his analysis of Turbo duplicata, and equally clear that Thompson understood it when he in turn passed along the essence of the matter.
  As for the relevant details, first of all, how well did Canon Mosely fare with Turbo duplicata ? Well enough, even in general terms, successfully arriving at the characteristic number (k) of 1.1806 compared to that of the pheidian spiral k = Phi 1/3 (1.1739)--as the latter scale applied to Mosely's illustration of the shell in question shows:

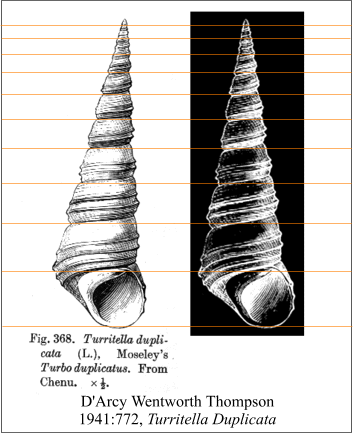
Fig. 22. Canon Mosely's Turritella Duplicata

Fig. 23.  Canon Mosely's Turritella Duplicata with the scale of the spiral k = Phi 1/3


But Mosely's treatment was far from simple, and to explain it in detail it is necessary to ask the reader to recall some of the steps taken so far in the present inquiry. Firstly, with respect to the astronomical side of the Pheidian planorbidae, it is necessary to remember that the growth factor k (Mosely's "Characteristic number") is the mean orbital inverse velocity (Vi); secondly, remember also the relationships between the mean planetary periods (T), the mean heliocentric distances (R) and the mean inverse velocities (Vi), especially relations 4 and 5 from Table 1: Mean Inverse Velocity (Vi) = T 1/3 and also Mean Inverse Velocity (Vi) =  R 1/2. Finally, note that the published "Velocity Expansions of the Laws of Planetary Motion" attributed to Galileo in the above mentioned paper were those given in the first line of the abstract, i.e.:

Kepler's Third Law of planetary motion: T2 = R3 ( T = period in years, R = mean distance in astronomical units ) may be extended to include the inverse of the mean speed Vi ( in units of the inverse of the Earth's mean orbital speed ) such that:  R = Vi 2 and T 2= R 3 = Vi 6

Additional relationships were also introduced, but the above represents the deducable essence of the matter--information that is quite sufficient for present purposes in so much as it leads readily enough to relations 4 and 5.  With this in mind we may now turn to Canon Mosley's unusual treatment of the spiral formations of Turbo duplicata recounted by Sir D'Arcy Wentworth Thompson (1917:773) 56

From the apex of a large Turritella (Turbo) duplicata a line was drawn across its whorls, and their widths were measured upon it in succession, beginning with the last but one. The measure ments were, as before, made with a fine pair of compasses and a diagonal scale. The sight was assisted by a magnifying glass. In a parallel column to the following admeasurements are the terms of a geometric progression, whose first term is the width of the widest whorl measured, and whose common ratio is 1.1804. [tables and data omitted ]
........
The close coincidence between the observed and the calculated figures is very remarkable, and is amply sufficient to justify the conclusion that we are here dealing with a true logarithmic spiral. Nevertheless, in order to verify his conclusion still further, and to get partially rid of the inaccuracies due to successive small measurements, Moseley proceeded to investigate the, same shell, measuring not single whorls but groups of whorls taken several at a time: making use of the following property of a geometrical progression, that "if u  represent the ratio of the sum of every even number (m ) of its terms to the sum of half that number of terms, then the common ratio (r ) of the series is represented by the formula:  r = (u - 1) 2/m .

So far, all of this is fascinating in its detail, exactitude and the amount of measurement involved, but it is next part that contains the hidden pearl. Given below in graphical form to match that presented by Sir D'Arcy Wentworth Thompson, the analysis proceeds as follows:

Canon Mosely and Turbo Dupicata

Notwithstanding the methodology, nor being being overly critical, it still seems an unnecessarily convoluted determination, and moreover, in spite of Mosely's confident statement that "It is scarcely possible to imagine a more accurate verification than is deduced from these larger admeasurements," the last relation "r = (1.389) 1/2 = 1.1806" is in fact incorrect--the actual result--1.1785--being on the other side of  Phi 1/3 (1.17398) . But what certainly is correct is the following restatement of the last two relations using accurate pheidian values, firstly to four decimal places (after Mosely), and secondly to ten:

Canon Mosely II

And yes, the key values given by Mosely (1.645 and 1.389) are indeed "larger admeasurements" compared to their pheidian counterparts--1.618 and 1.378 respectively. It is true that in the above r is applied in all cases, but it is still astronomically correct in the lower instance. Moreover, Mosely provided in thinly disguised form not only the Golden Ratio, but also by demonstrating the application of the cube and square roots the methodology leading to the mean sidered period (1.618033989), the mean heliocentric distance (1.378240772) and the corresponding mean inverse orbital velocity (1.173984997), i.e., the essence and the root of the Phi-series planetary framework with the last value also the characteristic number, or growth factor k for the shell in question. And having achieved this considerable goal, Mosley did indeed "with safety" not only annex the species Turbo duplicatus, he also passed on his insights in time-honoured tradition, ably assisted by Sir D'Arcy Wentworth Thompson, who in turn passed it on into the next century.

     Unfortunately, this part is missing in the abridged edition of On Growth and Form, as is the entire chapter on Phyllotaxis with its copious notes and related references.

   There is a great deal more, of course, that could be said concerning the details and the methodology applied to the fitting of spirals forms to shells and many other natural applications provided in Thompson's voluminous On Growth and Form. And indeed in other works that for a brief time seem to have flourished around the beginning of the last century. The above is included here because it epitomizes the darker, stumbling side of human progress. And also the realization that when Thomas Taylor (Introduction to Life and Theology of Orpheus) speaks of social decline, loss of knowledge in ancient times and the efforts to preserve it by those who, "though they lived in a base age" nevertheless "happily fathomed the depth of their great master's works, luminously and copiously developed their recondite meaning, and benevolently communicated it in their writings for the general good," that sadly, such times are still upon us. Thus, just as Sir Theodore Andrea Cook, who in the Curves of Life (1914) was unable to define the "well known logarithmic spiral" equated in 1881 with the chemical elements (see the previous section), neither Mosely nor Thompson were able write openly about the either the Golden Ratio or the Pheidian planorbidae. Nor unto the present day, it seems have others, for if not a forbidden subject per se, it long seems to have been a poor career choice, so to speak. Moreover, even after Louis Agassiz introduced Benjamin Pierce's phyllotaxic approach to structure of the Solar System in his Essay on Classification (1857) the matter was swiftly dispatched and rarely referred to again. A possibly momentous shift in awareness, shunted aside with greatest of ease, as the editor of Essay on Classification, (E. Lurie) explained in the short loaded footnote57discussed in the previous section. Nor it would seem, were the works of Arthur Harry Church (On the Relation of Phyllotaxis to Mechanical Law, 1904)58 or Samuel Colman (Nature's Harmonic Unity, 1911) 59allowed to take root. Nor again were the lines of inquiry laid out in Jay Hambidge's (Dynamic Symmetry 1920) permitted to have much on effect on the status quo either, not to mention Sir Theordore Andrea Cook's Curves of Life (1914) and the general the thrust of the many papers published during the previous century.

   Where does this obfuscation and stagnation leaves us now? Wondering perhaps where we might be today if the implications of the phyllotaxic side of the matter introduced in 1849 by Benjamin Pierce had at least been allowed to filter into the mainstream of knowledge with its wider, all-inclusive perspective concerning "life" as we currently understand it. The realization, perhaps, that we may indeed belong to something larger than ourselves, and that as an integral, living part of the Solar System rather than an isolated destructive apex, that we should conduct ourselves with more care and consideration towards all forms of life. Nor can we be in the least encouraged by the fact that since that time there have been almost continual outbreaks of local and international violence on Earth, including two major global conflicts with the imminent threat of another looming on the darkening horizon.*

   And here we might also ask whether humankind was truly well-served over the past century or so by the continued preservation of the status quo and the agendas of special interest groups, and because of this, whether we will even survive the madness of our times, let alone come of age.

* Written in 2002.  Matters have hardly improved since this time ...

END OF PART IVD2c

REFERENCES

  1. Winchester, Simon. The Map that Changed the World, Harper Collins, New York 2001.
  2. Thomson, Sir D'Arcy Wentworth. On Growth and Form, Cambridge University Press, Cambridge 1942; Dover Books, Minneola 1992.
  3. Huntley, H. E. The Divine Proportion: A Study of Mathematical Beauty, Dover, New York 1970.
  4. Kappraff, Jay. Connections:The Geometric Bridge Between Art and Science, McGraw-Hill, New York 1991.
  5. Arganbright, Deane. PHB Practical Handbook of Spreadsheet Curves and Geometric Construction, CRC Press, Boca Raton 1993.
  6. Cook, Sir Theodore Andrea. The Curves of Life, Dover, New York 1978; republication of the London (1914) edition.
  7. Colman, Samuel. Nature's Harmonic Unity, Benjamin Blom, New York 1971.
  8. Mosely, Rev. H. "On the geometrical forms of turbinated and discoid shells," Phil. trans. Pt. 1. 1838:351-370.
  9. Thomson, Sir D'Arcy Wentworth. On Growth and Form, Cambridge University Press, Cambridge 1942; Dover Books, Minneola 1992. 
  10. Nauman, C.F. "Ueber die Spiralen von Conchylieu," Abh. k. sachs. Ges. 1846; "Ueber die cyclocentrische Conchospirale u. uber das Windungsgetz von Planorbis corneus," ibid. I, 1849:171-195; "Spirale von Nautilus u. Ammonites galeatus, Ber. k. sachs. Ges. II, 1848:26; Spirale von Amm. Ramsaueri, ibid. XVI, 1864:21.
  11. Muller, J. "Beitrag zur Konchyliometrie," Poggend. Ann. LXXXVI, 1850:533; ibid. XC 1853:323.
  12. Macalister, A. "Observations on the mode of growth of discoid and turbinated shells," Proc. R.S. XVIII, 1870:529-532.
  13. Telescopium telescopium Linneaus 1758. Source: S. Peter Dance, Shells and Shell Collecting, Hamlyn Publishing Group, London 1972:32.
  14. Conus princeps f. lineolatus Valenciennes1832. Source: G. Paganelli,  Conus princeps f. lineolatus 1197 Index: www.coneshell.net
  15. Architectonica perspectiva Linneaus 1758. Source: S. Peter Dance, Shells and Shell Collecting, Hamlyn Publishing Group, London 1972:52-53.
  16. Harpa kajiyamai Rehder 1973.Source: Machiko Yamada, http://www.bigai.ne.jp/pic_book/data20/r001332.html Index: Micro shells Homepage
  17. Pedinogyra hayii Griffith & Pidgeon 1833 (Hay's Flat-whorled Snail). Source: Machiko Yamada, http://www.bigai.ne.jp/pic_book/data10/r000918.html  Index: Micro shells Homepage
  18. Planorbis corneus, Linnaeus 1758; Source: Martin Kohl, Freshwater Molluscan Shells: Pulmonata; Index: Freshwater Molluscan Shells
  19. Nautilus pompilus, Linnaeus 1758. Source: SEASHELLS. World of Nature Series, W.H. Smith, New York.
  20. Haliotis brazieri, Angas 1869. Source: D. L. Beechey, Haliotis brazieri; Index: Shells of New South Wales.  20a. Haliotis brazieri (smooth form variant)
  21. Haliotis scalaris, Leach 1814, Source: Machiko Yamada, http://www.bigai.ne.jp/pic_book/data20/r001967.html  Index: Micro shells Homepage
  22. Thompson, Sir D'Arcy Wentworth. On Growth and Form, 1992:
  23. Conus mercator, Linnaeus 1758 and Conus ammiralis f. hereditarius DA MOTTA, 1987. Source: G. Paganelli,  Index: www.coneshell.net
  24. Conus tulipa, Linnaeus 1758. Source: G. Paganelli, Conus tulipa 710  Index: www.coneshell.net
  25. Thompson, Sir D'Arcy Wentworth. On Growth and Form, 1992:816.
  26. Harpa goodwini. Source: Guido T. Poppe, Conchology http://www.conchology.uunethost.be/ 
  27. Clarke, Arthur H.The Freshwater Molluscs of Canada, National Museum of Natural Sciences, Ottawa 1981. 
  28. ibid., p.175.
  29. Kohl, Martin. Freshwater Molluscan Shells: Planorbidae ; Index: Freshwater Molluscan Shells
  30. Ovid, as quoted by Nicole Oresme in Du Ciel et du monde, Book II, Chapter 25, fols. 144a-144b, p.537.
  31. Liguus virgineus Linnaeus, 1758. Source: Harry Lee, jaxshells.org: http://www.jaxshells.org/ligver.htm  Index: http://www.jaxshells.org/
  32. Helisoma pilsbryi infracarinatum (Great Carinate Ramshorn Snail, Baker 1932). Source: Arthur H. Clarke.The Freshwater Molluscs of Canada, National Museum of Natural Sciences, Ottawa 1981:210.
  33. Helisoma (pierosoma) corpulentum corpulentum (Capacious Manitoba Ramshorn Snail , Say 1824). Source: Arthur H. Clarke. The Freshwater Molluscs of Canada, Ottawa 1981:206.
  34. Promenetus exacuous megas ( Broad Promenetus Dall, 1905. Source: Arthur H. Clarke.The Freshwater Molluscs of Canada, National Museum of Natural Sciences, Ottawa 1981:189.
  35. Thompson, Sir D'Arcy Wentworth, On Growth and Form, 1992:751-753.
  36. Hambidge, Jay. Dynamic Symmetry, Yale University Press, New Haven 1920:16-18.
  37. Kappraff, Jay. Connections:The Geometric Bridge Between Art and Science, McGraw-Hill, New York 1991:46. 
  38. Thompson, Sir D'Arcy Wentworth, On Growth and Form, 1992:791. 
  39. Haliotis parva,  Linnaeus 1758. Source: Molluscs.net: Haliotis parva; Index: http://www.molluscs.net/
  40. Harris, John N. "Projectiles, Parabolas, and Velocity Expansions of the Laws of Planetary Motion," JRASC, Vol 83, No. 3, June 1989:207-218.
  41. Wagner, Jeffrey K. Introduction to the Solar System, Holt, Rinehart & Winston, Orlando 1991:426.
  42. Marine decorated rhyton from Zakros (Crete). Wondrous Realms of the Aegean, selected by the editors, Lost Civilizations Series, Time-Life Books, Virginia 1993:110.
  43. Embossed, carved 12-inch rhyton from Zakros (Crete). Wondrous Realms of the Aegean, selected by the editors, Lost Civilizations Series, Time-Life Books, Virginia 1993:99.
  44. Bretagnon, Pierre and Jean-Louis Simon, Planetary Programs and Tables from -4000 to +2800, Willman-Bell, Inc. Richmond, 1986.
  45. Pierce, Benjamin. "Mathematical Investigations of the Fractions Which Occur in Phyllotaxis," Proceedings, AAAS, II 1850:444-447.
  46. Agassiz, Louis. Essay On Classification,  Ed. E. Lurie, Belknap Press, Cambridge 1962:127-128.
  47. Harris, John N. "Projectiles, Parabolas, and Velocity Expansions of the Laws of Planetary Motion, " JRASC, Vol 83, No. 3, June 1989:216.
  48. Raup, David. "Computer as aid in describing form in gastropod shells," Science 138, 1962:150-152. 
  49. Phillips, Tony and Stony Brook, "The Mathematical Study of Mollusk Shells" American Mathematical Society; AMS.ORG. 
  50. Thompson, Sir D'Arcy Wentworth. On Growth and Form, Cambridge University Press, Cambridge 1942; the complete unabridged reprint, Dover Books, Minneola 1992.
  51. Turritella duplicata, Source: Canon Mosely, in  Sir D'Arcy Wentworth Thompson, On Growth and Form, the complete unabridged edition, 1992:772.
  52. Euhoplites truncatus (Spath 1925). Source: Jim Craig: Euhoplites truncatus. Index: Fossils of the Gault Clay and Folkestone Beds of Kent, UK
  53. Dawkins, Richard. Climbing Mount Improbable, W.W. Norton, New York 1996:198:223. 
  54. _____________  Aruneus diademus Spider.Climbing Mount Improbable, Norton, New York 1996:58. 
  55. On Growth and Form, 1942:784. 
  56. On Growth and Form, 1942:773. 
  57. Lurie, E. (Ed.) Essay On Classification,  Belknap Press, Cambridge 1962:128.
  58. Church, Arthur Harry. On The Relation of Phyllotaxis to Mechanical Law, Williams and Norgate, London 1904; see also: http://www.sacredscience.com (cat #154).
  59. Colman, Samuel. Nature's Harmonic Unity, Benjamin Blom, New York 1971:3.
  60. Thatcheria mirabilis (Angas 1877). Source: Mathew Ward, Photographer; in Peter S. Dance, Shells, Stoddart, Toronto 1992.
  61.  Hildoceras bifrons, (Bruguière 1789).  Figure 1b2. Source: Hervé Châtelier, Ammonites et autres spirales - Hervé Châtelier.
  62. Dactylioceras commune (Sowerby 1815).  Figure 1Ca. Source: Hervé Châtelier, Ammonites et autres spirales.
  63. Porpoceras vortex (Simpson 1855).  Figure 1Cb.  Source: Hervé Châtelier, Ammonites et autres spirales.
  64. Protetragonites oblique-strangulatus (Kilian 1888).  Figure 1Cc. Source: Hervé Châtelier, Ammonites et autres spirales.
  65. Lytoceras cornucopia (Young & Bird 1822).  Figure 1Cd.  Source: Hervé Châtelier, Ammonites et autres spirales.
  66. Epophioceras sp. (Spath, 1923). Figure 1D. Source: Christopher M. Pamplin, Lower Jurassic Ammonites.
  67. Acanthopleuroceras valdani (D'Orbigny). Figure1d2. Source: Jean-ours and Rosemarie Filippi: Jurassic ammonites and fossil brachiopoda.
  68. Aegoceras (Aegoceras) capricornus (Schlotheim). Figure 1d3:  Source: Jean-ours and Rosemarie Filippi: Jurassic ammonites and fossil brachiopoda.
  69. Ethioceras raricostatum (Figure 1e).  Line drawing by Soun Vannithone, in Winchester, Simon. The Map that Changed the World, Harper Collins, New York 2001:1

For U.K. Ammonites, see:  FOSSILS OF THE GAULT CLAY AND FOLKESTONE BED OF KENT, UK  by the late Jim Craig, and  FOSSILS OF THE LONDON CLAY by Fred Clouter.

Copyright © 2002. John N. Harris, M.A.(CMNS). Last updated on July 20, 2004.
Ammonite graphics (Figures 1b2, 1c and 1d) added on April 29, 2003; Figure 21c on June 4 2003; Figure. 7b added 11 May, 2004; Figures 22a, 22b, and 1d3 added 17 July, 2004. Figures1 and 1e on 18 July, 2004.

RETURN TO THE MAIN PAGE

PREVIOUS SECTION

NEXT SECTION