For through analogy the universe is completely rendered one, this having the power of making things that are divided to be one, of congregating things that are multiplied, and connecting things that are dissipated. Hence theologists surveying the cause of these things in the Gods, enclose Venus with Mars, and surround them with Vulcanian bonds; the difference which is in the world being connected through harmony and friendship. All this complication and connection likewise has Vulcan for its cause, who through demiurgic bonds connects sameness with difference, harmony with discord, and communion with contrariety. [ Commentary of Proclus on the Timaeus of Plato, Translation by Thomas Taylor (1758-1835)]

The Grecian theology, which originated from Orpheus, was not only promulgated by him, but also by Pythagoras and Plato; who, for their transcendent genius, will always be ranked by the intelligent among the prodigies of the human race. By the first of these illustrious men, however, it was promulgated mystically and symbolically; by the second, enigmatically, and through images; and scientifically by the third. That this theology, indeed, was derived from Orpheus is clearly testified by those two great philosophic luminaries Iamblichus and Proclus. For by them we are informed, ' that what Orpheus delivered mystically through arcane narrations, this Pythagoras learned when he celebrated orgies in the Thracian Libethra, being initiated by Aglaophemus in the mystic wisdom which Orpheus derived from his mother Calliope, in the mountain Pangaeus.' This sublime theology, though it was scientifically disseminated by Plato, yet conformably to the custom of the most ancient philosophers, was delivered by him synoptically, and in such a way as to be inaccessible to the vulgar; but when, in consequence of the commencement of a degraded and barren period, this theology became corrupted through the negligence and confusion of its votaries, then such of his disciples as happened to live when it was thus degraded and deformed found it necessary to unfold it more fully, in order to prevent its becoming utterly extinct. The men by whom this arduous task was accomplished were the last of the disciples of Plato; men who, though they lived in a base age, possessed a divine genius, and who having happily fathomed the depth of their great master's works, luminously and copiously developed their recondite meaning, and benevolently communicated it in their writings for the general good. From this golden chain of philosophers, as they have been justly called, my elucidations of the present mystic hymns are principally derived: for I know of no other genuine sources, if it be admitted (and it must by every intelligent reader), that the theology of Orpheus is the same as that of Pythagoras and Plato.

To the latter group and the likes of Boethius [ca.500 CE], Oresme [ca.1350 CE], Galileo [ca.1600 CE], Kepler [ca.1618 CE], Thomas Stanley [ca.1650 CE], Thomas Taylor himself [ca.1800 CE] and more recently Kenneth Sylvan Guthrie [ca.1900 CE] we may also add the essential contribution of Arab scholars such as Averroes (1128-1198 CE), who not only preserved the original works through the Dark Ages, but also passed them on replete with their understanding. We may further observe here - the question of whether Pythagoras obtained his wisdom from Orpheus, Egypt or Chaldea notwithstanding - that long ago " Hermes Trismegistos " warned of the difficulties inherent in the custodianship of such knowledge, noting:

' There are those,' said Hermes, ' Who will thoroughly know all the secrets of my writings and interpret them, and even if they retain some of them for themselves alone, others among them that are for mankind's benefit they'll engrave on stelai and obelisks '. [Jack Lindsay, The Origins of Alchemy in Graeco-Roman Egypt, Trinity Press, London 1970:162]

Age-old conflicts, no doubt - of the ego and the intellect, and uncommon concern for self as opposed to the common good - but by the diligence of a few and the sublime ignorance of many, we have far more than engravings and monuments to rely on for enlightenment. The Neoplatonist Proclus [410-485 CE] was reputed to have said: "If I had it in my power, out of all the ancient books I would suffer to be current only the Oracles and the Timæus," yet he also noted in his own Commentaries that according to the divine Iamblicus, "the whole theory of Plato is comprehended in the Timæus and the Parmenides." Nevertheless, without context it would not necessarily be helpful to consider the latter a useful starting point. Moreover, although much of what follows here is necessarily "Pythagorean", a finer technical understanding would also appear to depend in part on the details of Babylonian planetary astronomy, which returns us to Chaldea and also to the Oracles venerated by Proclus.

Did Plato put the Earth in motion as he did the sun, the moon and the five planets which he called ' the instruments of time ' on account of their turnings, and was it necessary to conceive that the Earth ... was not represented as being (merely) held together and at rest but as turning and revolving, as Aristarchus and Seleucus afterwards maintained that it did, the former of whom stated this as only a hypothesis, the latter as a definite opinion?

Irrespective of prevailing Western beliefs and the status quo in general, Babylonian planetary astronomy (ca. 300 BCE, and possibly much earlier) was almost certainly both fictive and heliocentric; furthermore - judging from the accurate determination of varying planetary velocities, lines of apsides, the sidereal and synodic months, and many other technical considerations - it was also impressively advanced. Morever, it is rumoured that Plato in his later years regretted the predominance placed on the position of Earth and that he was also visited by a Chaldean who (so it is said) acquainted him with certain matters. What exactly came under consideration remains unknown, but as we shall see later, the Chaldean connection emerges once again in the context of Aristotle and the Fifth Element, which ties in with further technicalities associated with the Doctrine of the Timeaus, the quintessential constant of Alchemy, and the mean values inherent in Spira Solaris.

There are two senses in which the Timaeus is a ' myth ' or a ' story ' ...(in the first place) no account of the material world can ever amount to an exact and self-consistent statement on unchangeable truth. In the second place, the cosmology is cast in the form of a cosmogony, ' story ' of events spread out in time. Plato chooses to describe the universe, not by taking it to pieces in an analysis, but by constructing it and making it grow under our eyes. ... He introduced, for the first time in Greek philosophy, the alternative scheme of creation by a divine artificer, according to which the world is a work of art designed with a purpose. The Demiurge is a necessary part of the machinery, if the rational ordering of the universe is to be pictured as a process of creation in time. But the important point is that, no matter whether you prefer to analyze the world or to construct it piece by piece, the account can never be more than ' likely ', because of the changing nature of its object; it can never be revised and amended into exact truth.

All too often dismissed as myth alone, the Timeaus is rarely taken seriously by modern commentators, although Cornford's assessment suggests that it is more a matter of methodology than belief, and that the "likely" account of the construction can only be as precise as the tools provided in any event. As for revision and "amendation into the exact truth" it remains to be demonstrated - Heraclitean truisms notwithstanding - that where it matters most the information supplied in the Timaeus is technically valid and fundamentally sound, in spite of the cryptic nature of the presentation. Not that this has necessarily impeded understanding entirely in any case, for it seems that there were always some who managed to penetrate beyond the cover and the title, including Thomas Taylor in his own understanding of Proclus, although the latter's Commentary does in fact concern the shorter Timeaus the Locrian, as Proclus himself explains:

That the design of the Platonic Timaeus embraces the whole of physiology, and that it pertains to the theory of the universe, discussing this from the beginning to the end, appears to me to be clearly evident to those who are not entirely illiterate. For this very treatise of the Pythagorean Timaeus Concerning Nature, is written after the Pythagoric manner; and Plato being thence impelled, applied himself to write the Timaeus, according to Sillographus. On this account we have prefixed the treatise of Timaeus to these Commentaries, in order that we may know what the Timaeus of Plato says that is the same with what is asserted in the Treatise of Timaeus [the Locrian], what it adds, and in what it dissents. And that we may investigate not in a careless manner the cause of this disagreement. (Proclus on the Timaeus of Plato, Translated by Thomas Taylor, Kessinger Books, Kila, Introduction to Book I, Volume 1:xii).

Although interesting enough in their own right, the differences between the Timeaus and Timaeus the Locrian are not our immediate concern, nor is it the intention here to embark on a lengthy description of the Doctrine of the Timaeus itself. The subject is simply too vast to be discussed in its entirety here without additional groundwork, as may be gauged from Cornford's partial list of the contents of theTimaeus (17A through 68D):

17A-27B. Introductory Conversation.
27C-29D. Prelude. The nature and scope of Physics. (1) Being and Becoming. (2) The Cause of Becoming. (3) Model and copy, Physics only a ' likely story '

I. THE WORKS OF REASON
29D-30C. The motive of creation, The Demiurge.
30C-31A. The creator's model, The intelligible living Creature.
31A-31B. One world, not many.

The Body of the World
31B-32C. Why this consists of four primary bodies.
32C-33B. The world's body contains the whole of all the four primary bodies.
33B-34A. It is a sphere, without organs or limbs, rotating on its axis.

The World Soul
34A-34B. Summary. Transition to the World-Soul.
34B-34C. Soul is prior to body.
35A.------ Composition of the World-Soul.
35B-36B. Division of the World-Soul into harmonic intervals.
36B-36D. Construction of the circles of the Same and the Different and the planetary circles.
36D-36E. The world's body fitted to its soul.
36E-37C. Discourse in the World-Soul.
37C-38C. Time, the moving likeness of Eternity.
38C-39E. The Planets as instruments of Time.
39E-40B. The four kinds of living creature. The heavenly gods.
40B-40C. Rotation of the Earth.
40C-40D. The further movements of the heavenly bodies are too complicated for description here.

The Human Soul and Body
40d-41A. The traditional gods.
41A-41D. The address to the gods.
41D-42D. The composition of human souls. The Laws of Destiny.
42D-42E. Human souls sown in Earth and the planets.
42E-44D. The condition of the soul when newly incarnated.
44D-45B. Structure of the human body; head and limbs.
45B-46A. The eyes and the mechanism of vision.
46A-46C. Mirror images.
40C-47E. Accessory causes contrasted with the purpose of sight and hearing.

II. WHAT COMES ABOUT OF NECESSITY
47E-48E. Necessity. The Errant Cause. Reason and Necessity.
48E-49A. The Receptacle of Becoming.
49A-50A. Fire, Air, etc., are names of qualities, not of substances.
50A-50C. The Receptacle compared to a mass of plastic material.
50C-51B. The Receptacle has no qualities of its own.
51B-51E. Ideal models of Fire, Air, Water, Earth.
51E-52D. Summary description of the three factors: Form, Copy, and Space as the Receptacle.
52D-53C. Description of Chaos.
53C-55C. Construction of the figures of the four primary bodies.
55C-55D. Might there be five worlds?
55D-56C. Assignment of the regular figures to the four primary bodies.
56C-57C. Transformation of the primary bodies.
57C-57D. Each primary body exists in various grades of size.
57D-58C. Motion and Rest.
58C-61C. Varieties and compounds of the primary bodies. Water, liquid and fusible: melting and cooling of the fusible. Some varieties of the fusible type (metals): gold, adamant, copper. Solidification of fluids: water, hail, ice, snow, hoarfrost. Some varieties of the liquid type: juices. Varieties and compounds of earth: stone and earthenware, soda and salt; glass and wax.
61C-64A. Tactile qualities, as they appear to sensation and perception.
64A-65B. Pleasure and Pain.
65B-66C. Tastes.
66D-67A. Odours.
67A-67C. Sounds.
67C-68D. Colours.
[Cornford 1975:xi-xiii]

In seeking to establish the underlying framework of the Timaeus the present analysis remains largely with Cornford's translation - not only because of the detailed commentary and informative historical asides that accompany it, but also because of the avowed aim expressed in the Preface: "of persuading scholars that a Greek sentence means one thing rather than another." Bearing mind the obvious - that translations differ from author to author - the Benjamin Jowett version of the Timeaus is nevertheless available in its entirety from the Internet Classic Archive (Mit) while individual sections, e.g. Timaeus 17a (the beginning), Timaeus 52d onward (the detailed application of planes, triangles and solids), and Timaeus 59b (a condensed part of the alchemical analogy) may be accessed via the Perseus Project at Tufts. The present investigation is, however, largely limited to the preliminary building blocks provided by Plato for the construction of the "World Soul," but even here there is a considerable amount of groundwork required, as we shall see. The initial analysis necessarily includes the introduction of the Four Elements (initially Fire and Earth, followed by Air and Water) that are subsequently combined in "continued geometrical proportion" and later associated with specific triangles and solids (Timaeus 52d-56c). A further point of interest lies in the historical occurrence and apparent emphasis placed on particular numerical values and relationships in this context. This interest also embraces a number of pairings encountered not only in the Timeaus, but elsewhere in the writings of Plato and Aristotle, e.g., the "Even and the Odd," the "Divisible and the Indivisible," the "Limited and the Unlimited," etc. It is suggested that these pairings were not so much simple dichotomies as cryptic references to specific sequences, and that the latter must have been known and understood by those who invoked them. On a broader note, we may also observe that Aristotle (384-322 BCE, On the Soul, On Generation, The Heavens, Meteors, Physics, Metaphysics, etc.), Plotinus (205-270 CE, The Six Enneads), and Proclus (410-485 CE, The Commentaries, etc.) could hardly have written at length on such topics without a solid foundation on one hand and a definite purpose on the other. Even so, it is only after the mathematical details are understood that such works begin to take on specific meaning and relevance. It is also apparent here that when the latter refer to the "soul" that it is not the later, restricted Christian concept that is under consideration, but the dynamic, all-encompassing "World-Soul" of the Timaeus of Plato. Even so, it would appear that some flexibility was originally intended concerning such matters in general, as Proclus relates in Book II of his Commentaries, i.e., "Let therefore this universe be denominated by us, all heaven, or the world, or whatever other appellation it may be especially adapted to receive." Further information concerning the relationship between the Timaeus of Plato, the Hermetic Tradition, and later Christian components may be found in The J. R Ritman Library.
Remaining in our present context, however, while we may recognize that both Timeaus the Locrian and Plato's Epinomis may be considered by some to be of "doubtful" (i.e., later) authenticity, it is nevertheless towards the conclusion of the latter that Plato's methodology is more clearly annunciated:

We must do what we can to enumerate the subjects to be studied and explain their nature and the methods to be employed, to the best of the abilities of myself who am to speak and you who are to listen--to say, in fact, how a man should learn piety, and in what it consists. It may seem odd to the ear, but the name we give to the study is one which will surprise a person unfamiliar with the subject--astronomy. Are you unaware that the true astronomer must be a man of great wisdom? I do not mean an astronomer of the type of Hesiod and his like, a man who has just observed settings and risings, but one who has studied seven out of the eight orbits, as each of them completes its circuit in a fashion not easy of comprehension by any capacity not endowed with admirable abilities. I have already touched on this and shall now proceed, as I say, to explain how and on what lines the study is to be pursued. And I may begin the statement thus. The moon gets round her circuit most rapidly, bringing with her the month, and the full moon as a first period. Next we must observe the sun, his constant turnings throughout his circuit, and his companions. Not to be perpetually repeating ourselves about the same subjects, the rest of the orbits which we enumerated above are difficult to comprehend, and to train capacities which can deal with them we shall have to spend a great deal of labor on providing preliminary teaching and training in boyhood and youth. Hence there will be a need for several sciences. The first and most important of them is likewise that which treats of pure numbers--not numbers concreted in bodies, but the whole generation of the series of odd and even, and the effects which it contributes to the nature of things. When all this has been mastered, next in order comes what is called by the very ludicrous name mensuration, but is really a manifest assimilation to one another of numbers which are naturally dissimilar, effected by reference to areas. Now to a man who can comprehend this, it will be plain that this is no mere feat of human skill, but a miracle of God's contrivance. Next, numbers raised to the third power and thus presenting an analogy with three-dimensional things. Here again he assimilates the dissimilar by a second science, which those who hit on the discovery have named stereometry [the gauging of solids], a device of God's contriving which breeds amazement in those who fix their gaze on it and consider how universal nature molds form and type by the constant revolution of potency and its converse about the double in the various progressions. The first example of this ratio of the double in the advancing number series is that of 1 to 2; double of this is the ratio of their second powers [ 4 ], and double of this again the advance to the solid and tangible, as we proceed from 1 to 8 [ 1, 2, 2², 2 ³ ]; the advance to a mean of the double, that mean which is equidistant from lesser and greater term [the arithmetical], or the other mean [the harmonic] which exceeds the one term and is itself exceeded by the other by the same fraction of the respective terms-- these ratios of 3 : 2 and 4 : 3 will be found as means between 6 and 2: why, in the potency of the mean between these terms [ 6 x 2 ], with its double sense, we have a gift from the blessed choir of the Muses to which mankind owes the boon of the play of consonance and measure, with all they contribute to rhythm and melody.
So much, then, for our program as a whole. But to crown it all, we must go on to the generation of things divine, the fairest and most heavenly spectacle God has vouchsafed to the eye of man. And: believe me, no man will ever behold that spectacle without the studies we have described, and so be able to boast that he has won it by an easy route. Moreover, in all our sessions for study we are to relate the single fact to its species; there are questions to be asked and erroneous theses to be refuted. We may truly say that this is ever the prime test, and the best a man can have; as for tests that profess to be such but are not, there is no labor so fruitlessly thrown away as that spent on them. We must also grasp the accuracy of the periodic times and the precision with which they complete the various celestial motions, and this is where a believer in our doctrine that soul is both older and more divine than body will appreciate the beauty and justice of the saying that ' all things are full of gods ' and that we have never been left unheeded by the forgetfulness or carelessness of the higher powers. There is one observation to be made about all such matters. If a man grasps the several questions aright, the benefit accruing to him who thus learns his lesson in the proper way is great indeed; if he cannot, 'twill ever be the better course to call on God. Now the proper way is this--so much explanation is unavoidable. To the man who pursues his studies in the proper way, all geometric constructions, all systems of numbers, all duly constituted melodic progressions, the single ordered scheme of all celestial revolutions, should disclose themselves, and disclose themselves they will, if, as I say, a man pursues his studies aright with his mind's eye fixed on their single end. As such a man reflects, he will receive the revelation of a single bond of natural interconnection between all these problems. If such matters are handled in any other spirit, a man, as I am saying, will need to invoke his luck. We may rest assured that without these qualifications the happy will not make their appearance in any society; this is the method, this the pabulum, these the studies demanded; hard or easy, this is the road we must tread. [Epinomis, 989d-992a, Translated by A.E. Taylor, The Collected Dialogues of Plato, Princeton University Press, Princeton, 1982:1530-31]

The explicit mention of "the generation of things divine" in the above passage is encouraging, as is the emphasis on "the whole generation of the series of odd and even, and the effects which it contributes to the nature of things," although at present the precise meaning of the latter remains unclear. Nevertheless, we have encountered many of the above numbers and relations before, especially the Double Interval, the ratios 3 : 2 and 4 : 3 and the product 6 x 2 (12) mentioned in Nicole Oresme's Le Livre du ciel et du monde (ca. 1375 CE) as discussed in the previous section (Spira Solaris and the Middle Ages). Although the Triple Interval is absent in the above, as far as a working example of the Harmonic Law is concerned - the square of the mean period of revolution equaling the cube of the mean heliocentric distance - it is the Double Interval [ 1, 2, 2², 2³ ] = [ 1, 2, 4, 8 ] that provides the first integer pair, specifically for a mean distance of 4 (with respect to unity, i.e., the first value in the interval) and a corresponding mean period of revolution of 8 years, thus 4³= 8 ². Moreover, it is undoubtedly a fundamental necessity that the periods of revolution must first be determined accurately before the Third (or Harmonic) Law of planetary motion can be applied to obtain the corresponding mean distances, thus the text states somewhat cryptically with respect to the "soul" (period) being "older and more divine" than the "body" (distance):

We must also grasp the accuracy of the periodic times and the precision with which they complete the various celestial motions, and this is where a believer in our doctrine that soul is both older and more divine than body will appreciate the beauty and justice of the saying that ' all things are full of gods ' and that we have never been left unheeded by the forgetfulness or carelessness of the higher powers.

Those unconvinced that the "Harmonic" Law was known in antiquity may wish to refer to the discussion concerning of this topic in the previous section, and/or consider the import of Aristotle's statement in Metaphysics, Book XIV, Ch. 6 [1093a. Trans. W. D. Ross]:

(Since) all things must share in number, it must follow that many things are the same, and the same number must belong to one thing and to another. Is number the cause, then, and does the thing exist because of its number, or is this not certain? E.g. the motions of the sun have a number, and again those of the moon, - yes, and the life and prime of each animal. Why, then, should not some of these numbers be squares, some cubes, and some equal, others double? There is no reason why they should not, and indeed they must move within these limits, since all things were assumed to share in number.

Although obvious enough in retrospect, it would appear that the Law was in need of reinforcement (if not clarification) from time to time, and thus Galileo - the source of the velolcity component to the present discourse - who, applying Pythagorean terms in dialectic style in The Dialogues Concerning Two New Sciences (First Day,134-135) states: "similar solids are to each other in the sesqualteral ratio to their surfaces," and further: "the surfaces of similar solids are in the duplicate ratio of their sides and also the proposition which proves that the volumes are in the triplicate ratio of their sides." Finally and succinctly, Galileo's commentator explains the sesquialteral ratio (3 : 2) with an expanded echo of Aristotle's remarks:

For if one quantity is the cube of something of which another quantity is the square, does it not follow that the cube is the sesquialteral of the square? Surely. Now if the surface varies as the square of its linear dimension while the volume varies as the cube of these dimensions may we not say that the volume stands in sesquialteral ratio to the surface?

The Dialogues Concerning Two New Sciences was published "accidently" in Holland in 1638 in response to a complete ban against all publication of Galileo's work in Italy. There exist, however, a number of oddities associated with this final publication, for the title was not of Galileo's own choosing and nor apparently was it to his liking. Furthermore, there was supposedly a Fifth Section to the work which was either never completed or simply never saw the light of day. But be that as it may, Galileo's many difficulties no doubt serve to emphasize what is perhaps one of the underlying problems associated with much of the historical side of the present inquiry. The harmonic law and indeed general progress in coming to terms with the structure of the Solar System depend on the understanding of the heliocentric concept and the true nature of planetary motion, i.e., elliptical obits with attendant varying velocities. Both oppose long-entrenched Establishment beliefs firmly anchored on geocentric theory and uniform circular motion. Given such institutionalized opposition, it is hardly surprising that little real understanding of the Timeaus managed to filter into the mainstream of contemporary knowledge. But that is not the only reason, for as one explores further it becomes clear that the work represents a complex treatment that requires much explanation, many tools and not least of all, a high degree of intellection. Moreover, it is not surprising that the heliocentric aspect is unclear in the Timaeus and elsewhere, or that ambiguous, difficult passages abound in related works. Nor indeed can we completely rule out the heliocentric concept even when we come across specific references to the equality for the periods of the Sun, Mercury and Venus, which are normally understood in geocentric terms. For example, according to the "Pythagoreans":

Concerning the course of revolution of the planets, they affirm the great year to the revolution of Saturn, for the rest of the planets absolve their periods in a shorter time but Saturn is no less than thirty years, Jupiter twelve years, Mars two; the Sun, Mercury or Venus, as the Sun [or to speak more exactly, Mercury in three months, Venus in eight] the moon in being next to Earth soonest, in a month." [Thomas Stanley, Pythagoras: His Life and Teaching, Philosophical Research Society, Los Angeles, 1970:537; emphasis supplied]

Here the emphasized periods are undoubtedly approximations for the mean sidereal periods of revolution for both Mercury and Venus, while for his part Proclus also informs us in his Commentary on the Timaeus that according to the Pythagoreans:"the elements may be surveyed in the heavens in a twofold respect, in one way indeed prior to the sun, and in another after it." Subterfuges of this kind are hardly surprising, for it is far from certain that any open, detailed heliocentric treatment of the Solar System would have been tolerated in certain eras, let alone permitted to survive intact against the institutionalized geocentric primacy of the Dark Ages. The same may also be said concerning Pythagorean doctrines in general, for they too may well have survived only because they were largely misunderstood or even perhaps deemed to have been innocuous and primitive. Either way, we are fortunate, for the surviving material does indeed provide further insights and elucidation concerning the fundamental Pythagorean concepts embedded in the Timaeus itself.

Cornford (1975:50), in discussing the terminology applied in the above notes that:

Some of the older terms in Greek mathematics have biological associations:.... skin for surface, ..power for square, ... growth for dimension, ... body for solid. They were taken from living things and fit in with the Pythagorean conception of the unit as the ' seed or eternal root from which ratios grow or increase reciprocally either side ' (Iambl. in Nichom., p. 11 Pistelli). The unit contains potentially all the forms of even and odd number 'as being a sort of fountain or root of both kinds.'

whereas, according to Pythagorean doctrines:

Number is the first principle, a thing which is undefined, incomprehensible, having in itself all numbers which could reach infinity in amount. And the first principle of numbers is in substance the first Monad, which is a male monad, begetting as a father all other numbers. Secondly, the Dyad is a female number, and the same is called by the arithmeticians even . Thirdly, the Triad is a male number; this the arithmeticians have been wont to call odd. Finally, the Tetrad is a female number, and the same is called even because it is female. .... Pythagoras said this sacred Tektractys is: ` the spring having the roots of ever-flowing nature.' .. The four parts of the Decad, this perfect number, are called number, monad, power and cube. And the interweavings and minglings of these in the origin of growth are what naturally completes nascent number; for when a power of a power; and a cube is multiplied on a cube, it is the power of a cube; and when a cube is multiplied on a cube, the cube of a cube; thus all numbers, from which arise the genesis of what arises, are seven: number, monad, power, cube, power of a power, power of a cube, and cube of a cube. [Hippol., Phil,. 2. Dox. 355, PYTHAGOREAN SOURCES & FRAGMENTS, Kenneth Sylvan Guthrie, Phanes Press, Grand Rapids, Michigan 1988:312]

Taken individually, each tetrad might at first acquaintance appear simplistic, but when applied as an integral group to the "living" structure of the Solar System with its "body, and three parts of the soul" the given sets take on far greater complexity, especially since many are also invoked one way or another in the construction of the "World Soul" in the Timaeus, where the "simple bodies" Fire and Earth are applied in the initial phase of the construction, i.e.

Now that which comes to be must be bodily, and so visible and tangible; and nothing can be visible without fire, or tangible without something solid, and nothing solid is without earth. Hence the god, when he began to put together the body of the universe, set about making it of fire and earth. But two things alone cannot be satisfactorily united without a third; for there must be some bond between them drawing them together. And of all bonds the best is that which makes itself and the terms it connects a unity in the fullest sense; and it is of the nature of a continued geometrical proportion to effect this most perfectly. For whenever of three numbers, the middle one between any two that are either solids (cubes) or squares is such that, as the first is to it, so is it to the last, and conversely as the last is to the middle, so is the middle to the first, then since the middle becomes first and last, and again the last and first becoming middle, in that way all will necessarily come to play the same part towards one another, and by doing so they will make a unity. Now it had been required that the body of the universe should be a plane surface with no depth, a single measure would have been enough to connect its companions and itself; but in fact the world was to be solid in form, and solids are always conjoined, not be one mean, but by two. Accordingly the god set water and air between fire and earth, and made them, so far as was possible, proportional to one another, so that as fire is to air, so is air to water and as air is to water, so is water to earth, and thus he bounded together the frame of a world visible and tangible. For these reasons and from such constituents, four in number, the body of the universe was brought into being, coming into concord by means of proportion, and from these it acquired Amity, so that coming into unity with itself it became indissoluble by any other save him who bound it together. (Timaeus, 31b-32c, Plato's Cosmology: The Timaeus of Plato, Translated by Francis MacDonald Cornford, Bobbs-Merrill, Indianapolis, 1975:43-44, emphases supplied)

Omitting the references to the elements "Fire" and "Air" for the present, we can see that the stated construction is undoubtedly applicable to the Phi-Series planetary framework throughout, e.g., taking the corresponding four phi-series periods: [ 1, 1.61800989, 2.618033989, 4.236067978 ], 1 is to 1.61800989 as 1.61800989 is to 2.61800989, as 2.61800989 is to 4.236067978, whereas the increment and the fundamental constant by which the planetary periods (planets and synodics) increase is Phi itself. Or putting it another way, the division of a line into the Golden Section, i.e., into two unequal parts, such that the relationship between the smaller part to the larger part is the same as the relationship between the larger part and the whole can be repeated indefinitely with a sliding middle component which always maintains the same relationship to either extremity. This is, of course, an example that pertains to the end product rather than the preliminary construction. However, since the combination of the Pythagorean Tetradic sets: numbers: [ 1, 2, 3, 4 ] and simple bodies: [ Fire, Air, Water, Earth ] produces the following numerical assignments: 1 = FIRE, 2 = AIR, 3 = WATER, 4 = EARTH and the initial pairing in the Timaeus is Fire (1) and Earth (4) we may proceed by noting that these two values meet a special requirement that combines arithmetical and harmonic means as discussed by Sir Thomas Heath below:

The anonymous author of a scholium to Book v. (Euclid, ed. Heiberg, Vol. v. p.280), who is perhaps Proclus, tells us that "some say" this Book, containing the general theory of proportion which is equally applicable to geometry, arithmetic, music, and all mathematical sciences, "is the discovery of Eudoxus, the teacher of Plato." Not that there had been no theory of proportion developed before his time; on the contrary, it is certain that the Pythagoreans had worked out such a theory with regard to numbers, by which must be understood commensurable and even whole numbers (a number being a "multitude made up of units," as defined in Eucl. vii). Thus we are told that the Pythagoreans distinguished three types of means, the arithmetic, the geometric and the harmonic means, the geometric mean being called proportion par excellence; and further Iamblicus speaks of the "most perfect proportion consisting of four terms and specially called harmonic," in other words, the proportion: a : (a + b)/2 = 2ab/(a + b) : b which is said to be a discovery of the Babylonians and to have been first introduced into Greece by Pythagoras (Iamblicus, Comm. on Nicomachus, p.118). Now the principle of similtude is one which is presupposed by all the arts of design from their very beginnings; it was certainly known to the Egyptians, and it must certainly have been thoroughly familiar to Pythagoras and his school. [ Introductory Note to Book V, The Thirteen Books of Euclid's Elements, Translation and Commentary by Sir Thomas Heath, Dover Publications Inc., p.112 ]

We already know that the Arithmetic, Geometric and Harmonic Means are integral parts of Spira Solaris, which includes all of the following:

The Golden Rule of Arithmeticall Whole Numbers ("The Rule of Three") is found in an obscure booklet entitled: The Art of Tenths by Robert Norton (ca.1600 CE). Although dealing with decimal operations, towards the end of the discourse the Golden Rule - which is not to be confused with "Do unto others as you would have others do unto you" - is formulated as "The Fifth Probleme" to be solved as follows:

Three Termes of Arithmeticall Numbers, being given to finde their proportionall Terme.
Explication propounded: Be the three termes given 2, 3, 4. Explication required: To finde their fourth proportional Terme:
that is to say, in such Reason to the third terme 4, as the second terme 3, is to the first terme 2.
Construction: Multiply the second terme 3, by the third terme 4. {this} giveth the product 12: which dividing by the first terme 2, giveth the Quotient 6:
I say that 6 is the fourth proportional terme required.
Demonstration: there is from 6 to 4, Reason sesquialter, and the same Reason is there from 3 to 2: therefore 6 is the fourth proportional terme to be demonstrated.
Conclusion: three Arithmeticall numbers being given, wee have found their fourth proportionall term required. [Robert Norton, The Art of Tenths, 1608]

Here again we encounter the numbers 2, 6 and 12, the sesquialter ratio, continued proportion, and in the example given, three of the four fundamental elements grouped in due order (2, 3, 4). The problem apparently requires the determination of the next proportional term with the first three given, and to this end the solution is obtained from the product of the second and third terms divided by the first. The result is given as 6, thus the series is now 2, 3, 4, 6, etc.. However, the very simplicity of the computation belies its grandiose status, for why should this simple operation be singled out for special consideration and assigned the title "Golden Rule of Arithmeticall whole numbers"? Apart from its origins (which are unstated) we may note that the operation when applied to the Phi-Series periods does in fact produce the next value in the series exactly, thus we may add it to our list of mathematical features, specifically, for three successive periods: P_n, P_{n + 1}, P _{n + 2}, the fourth value in the Series ( P_{n + 3} ) is obtained from the relation provided above by Robert Norton: P_{n + 3} = ( P_{n + 1} )( P_{n + 2} )/P_n. For example, following the three periods for Jupiter though Saturn, the next synodic period (the fourth number in the series) is 46.978713764 years. Whereas by applying the Rule of Three we also have 17.94427191 x 29.03444185 / 11.09016994 = 46.97871376 or, since we are dealing with the Phi Series:
 Phi ⁸ = (Phi ⁶ x Phi ⁷)/Phi ⁵ = Phi ¹³/Phi ⁵ = Phi ⁸, etc, with Fibonacci numbers occurring as exponents. In actual fact, the "Golden Rule of Arithmeticall Whole Numbers" is the "Rule of Three" in more than one sense, for it not only applies to the Phi-Series mean periods, but also to the mean distances and the mean velocities.

In the potency of the mean between these terms [ 6 x 2 ], with its double sense, we have a gift from the blessed choir of the Muses to which mankind owes the boon of the play of consonance and measure, with all they contribute to rhythm and melody.

Seeking a "double sense" and mean values between 2 and 6 leads to the understanding that among all the various types of means and all integer values between 2 and 6 there are in fact two types of mean values that produce the same integer value 3, namely the Harmonic Mean: ( 2 x 2 x 6 )/(2 + 6) = 3 and the Synodic Mean: ( 2 x 6 )/( 6 - 2 ) = 3. While the Harmonic Mean might well represent the first introductory step and also be important in its own right, it is nevertheless the Synodic Mean (the Product of two sidereal periods divided by their Difference) that undoubtedly represents the cornerstone of the matter, for it was the introduction of synodic motion in the initial investigation (see Section Two) that resulted in the quadratic equation that determined the value of the required constant of linearity - phi itself - 1.618033989.

The things of which he composed soul and the manner of its composition were as follows: ( 1 ) Between the indivisible Existence that is ever in the same state and the divisible Existence that becomes in bodies, he compounded a third for of Existence composed of both. ( 2 ) Again, in the case of Sameness and in that of Difference, he also on the same [principle made a compound intermediate between that kind of them which is indivisible and the kind that is divisible in bodies. ( 3 ) Then, taking the three he blended them all into a unity, forcing the nature if the Difference, hard as it was to mingle, into union with Sameness, and mixing them together with Existence. [35B]. And having made unity of the three, again he divided this whole into as many parts as was fitting, each part being a blend of Sameness, Difference, and Existence.... [Timaeus 34B-35B, Cornford 1975:59-66]
This whole fabric, then, he split lengthwise into two halves; and making the two cross one another at their centres in the form of a letter X, he bent each around into a circle and joined it up, having each meet itself and the other at a point opposite to that where they had been brought into contact. He then comprehended them in motion that is carried round uniformly in the same place, and made the one the outer, the other the inner circle. The outer movement he named the movement of the Same; the inner, the movement of the Different. The movement of the Same he caused to revolve to the right by way of the side; the movement of the different to the left by way of the diagonal. [Timaeus 36B-36C, Cornford 1975:73]

Although there are exceptions (e.g., in the cases of Earth and Neptune), the synodic cycle does generally fit between co-orbital bodies thus the circle of the "different" will indeed usually lie inside the outermost circle of the "same". As for the meaning of the initial sentence: " Between the indivisible Existence that is ever in the same state and the divisible Existence that becomes in bodies," it is necessary to recall that in keeping with the Soul-Body-Spirit assignments, "Soul" corresponds to time (i.e., period), "Body" to distance (and "Spirit" to velocity). Thus, whereas a quantity representing heliocentric distances ("bodies") can be subdivided at will and corresponding sidereal periods ("soul") may be determined from the application of the Harmonic law, the reverse procedure does not hold. Individual periods of revolution - circles of the "Same" - may, of course, be applied to obtain corresponding heliocentric distances, but revolutions cannot be subdivided without modifying their form and thus voiding the application of the harmonic law. Further explanations concerning multiple meanings ascribed to "soul" and "body" in this context are provided by another Neoplatonist (Numenius of Apamea, 2^nd Century CE) as follows :

Because bodies, according to their own nature, are changeable, inconstant, and infinitely divisible, and nothing unchangeable remains in them, there is evidently need of a principle that would lead them, gather them, and bind them fast together; and this we name Soul. If then the soul were a body of any kind of constitution, even if it were as small as (an atom,) what would then hold that together ? For we said that every body needed some principle that would hold the body together, and so on into infinity, until we should reach the incorporeal. ....Should it be said, however, that because bodies have three dimensions, then must also the soul, as it penetrates the whole body, be of triple extension, and therefore in any case be a body, then would we have to answer that although every body has three dimensions, yet not everything that has three dimensions is a body. For quantity and quality, which in themselves are incorporeal, may under certain circumstances be reckoned quantatively. Likewise the soul, which in itself is non-extensive, might be considered as tridimensional in case that by chance it had happened into something tridimensional .....Before those, who earlier than we have attempted to explain the nature of the soul mathematically as some medium between the natural and the supernatural, it is asserted by those who call the soul a number, that it consists of unity, as something indivisible, and of the indefinite doubleness (manifold) as something divisible. Others, however, who conceive of the soul as of a geometrical figure, insist that it consists of a point and the divergence (either a locus and the divergence of two lines, or a centre and the radius of a circle); of which the first is indivisible, and the second divisible. Of the first opinion are the partisans of Aristander, Numenius, and the majority of the expounders; of the second opinion is Severus. [The Neoplatonic Writings of Numenius, Collected and translated by Kenneth.Sylvan.Guthrie, Vol. VI, Great Works of Philosophy (ed. Ed. Robert Navon) Selene Books, Lawrence, Kansas 1987: 44-46, emphases supplied]

And finally, from the same erudite source we have what might constitute a more direct reference to both Phi and the seven luminaries:

Theodorus, the philosopher of Asine, was permeated with the teachings of Numenius. He spins dreams about the birth of the soul in a rather original manner, busying himself with letters, their form, and numbers . . . making the universal or geometrical number out of the (fourfold) soul, inasmuch as the group of seven finds itself in the name of the soul. [Guthrie, The Neoplatonic Writings of Numenius, p.60, emphases supplied]

Here we touch once again upon the degree of complexity running through much of theTimaeus - complexity that arises from the need for intellection, perception by way of the senses, and the resulting applied methodology, or, as Henry Chadwick (1981:82) put it while discussing Boethius and music, " the Soul's threefold power to think, to perceive, and then acquire a skill."
Returning to Phi and the passage in the Timaeus, we do know that this ubiquitous constant provides the increment for all the successive periods in the phi-series based planetary framework, i.e., the planet-synodic-planet increments, while phi squared = 2.618033989 provides the corresponding planet-to-planet increments alone. Taken together this pair of constants may be compared with the approximations provided by the two initial values (periods) between Fire and Earth, i.e., 1.6 and 2.666* respectively, especially since the latter value represents the synodic mean period (lap cycle) between 1.6 and 4, i.e., (1.6 x 4)/(4 - 1.6) = 2.666*. Thus we obtain the tetradic set: Fire (1), Air (1.6), Water (2.666*) and Earth (4), which for rounded values brings us back to the integer set [ 1, 2, 3, 4 ]. However, further synodic means may also be obtained, specifically - as alluded to in the text (in addition to simplistic arithmetical increases) - between Fire and Air, Air and Water, and Water and Earth, i.e.,

Although we are able to equate the Harmonic, Synodic and Golden Means with material provided in the Epinomis and Timaeus, apart from such phrases as "continued geometric proportion," there is still no explicit mention of Phi itself in either work. But is this because it is entirely absent, or because it is buried deeply within, and can only be brought to the surface by the applied effort and knowledge of the reader? And not least of all in our present context, what might the elements "Fire, Air, Water and Earth" represent - if anything - from a fictive, kinematic point of view, especially with respective to the structure of the Solar System on one hand, and the Phi-Series planetary framework on the other?
We may begin here by noting that the four elements have been traditionally and alchemically associated with the following qualities: Fire (Hot and Dry), Air (Moist and Hot), Water (Wet and Cold) and Earth (Cold and Dry), which are appropriate enough to categorize the first four planets (Mercury, Venus, Earth and Mars) according to their predominant physical attributes. In other words, from both descriptive and heliocentric viewpoints, the element "Fire" pertains to the first planet Mercury (Hot and Dry), "Air" to the second planet Venus (Moist and Hot), like it or not, "Water" to the third planet Earth (Wet and Cold), leaving the element "Earth" to be assigned in due order to the last and fourth terrestrial planet Mars (Cold and Dry):

The Earth, fixed at the centre, becomes the hearth of the gods, and the boundary of darkness and day, producing both settings and risings, according to the cuttings off (made by) the things that form the boundary, as we circumscribe by a cutting off the things of earth, sufficient for sight. And it is the oldest of bodies within the circle of heaven. And neither has Water at any time been produced without Earth, nor Air without moisture; nor could Fire continue without moisture and the materials which it burns; so that (the Earth) is fixed, as the root and base of all other substances, upon its own balance. [emphases supplied]

In conclusion, Earth is the spiritual principle of stable but inflexible synthesis, the passive imposition of form, and the foundation of physical being. The Element is associated with Hera, as protectress of the stable foundation of fertility, and with the Earth Goddesses Demeter and Gaia.

Now let this be called a scalene (triangle); but the other, the half of a square, (be considered) the principle of the constitution of the Earth....For the Earth alone has the half-square, as its peculiar element; and this is the element of the (three) other substances, Fire, Air, and Water. [ The Treatise of Timaeus the Locrian on the Soul of the World and Nature, The Works of Plato: A New and Literal Version, Vol. VI, George Burges, George Bell & Sons, London, 1876:158]

 

The Pythagoreans considered the figure seven as the image and model of the divine order and harmony in nature. It was the number containing twice the sacred number three or the "triad," to which the "one" or the divine monad was added: 3 + 1 + 3. As the harmony of nature sounds on the key-board of space, between the seven planets, so the harmony of audible sound takes place on a smaller plan within the musical scale of the ever-recurring seven tones. Hence, seven pipes in the syrinx of the god Pan (or Nature), their gradually diminishing proportion of shape representing the distance between the planets and between the latter and the earth--and, the seven-stringed lyre of Apollo. Consisting of a union between the number three (the symbol of the divine triad with all and every people, Christians as well as pagans) and of four (the symbol of the cosmic forces or elements), the number seven points out symbolically to the union of the Deity with the universe; this Pythagorean idea was applied by the Christians--(especially during the Middle Ages)--who largely used the number seven in the symbolism of their sacred architecture. (Theosophy, June 1880)

The numbers and related symbols referred to here necessarily impinge on the present investigation, but it is too early to delve into their historical usage and significance except to note that both the equilateral triangle and the square feature are given prominance in later alchemical contexts (see the Engraving from I.C. H., Das Hermes Trimegists, Leipsig, 1782 and the Sixth woodcut from the series in Basil Valentine's Azoth).
Returning to the element "Aether," it seems likely that the requirement for this fifth element belongs to a fuller understanding of synodic motion on one hand and the heliocentric concept on the other. Which in turn may have generated, perhaps, the suspicion (or awareness) - as indicated by the Phi-Series planetary framework - that planet Earth is not necessarily occupying a "normal" planetary region at all, but rather, that it is located in the synodic position between Venus and Mars (see Sections Two and Three for details). How this might have come about historically and the difficulties that would attend the introduction of a fifth element are summarized by Proclus as follows:

Some of the Platonists, being impelled by the assertions of Aristotle, extend through the whole world one passive matter, not at all different from that of the heavens, and in consequence of embracing certain barbaric opinions, give to the world a fifth body, and refer the doctrine concerning it to Plato. For Aristotle, following these opinions, introduced a fifth element. And this in a certain respect he obscurely signifies, adducing the observations of the Barbarians as a testimony of the perpetuity and sameness of the motion of aether. But others assert, that the heavens are of a different essence, as having a different form of life, a more simple motion, and a more perpetual nature; but that Plato is now speaking about the sublunary elements, and adorns these by analogies. These men indeed, speak rightly, both with respect to things, and the opinion of Plato, in asserting that the nature of the heavens is different from mutable, and in short, material things; but at the same time they neglect the Platonic words, in which the philosopher says, that ' the Demiurgus bound together and constituted the heavens [or the universe] through the analogy of the four elements;' and again, in another place, ' that he elaborated the idea of the stars, for the most part from fire.'
Let us therefore, if you are willing, preserving the opinions of both these men, perspicuously show, that the whole world consists of the four elements, and that the heavens are of a different essence [from the sublunary regions]. And in the first place let us discuss the latter. For it is necessary, either that the heavens, should be entirely different from the four elements, being, as some say, a fifth element; of that the heavens should consist of the four elements; or from some one of the four; or from more than one. And if the heavens consist of the four, they either consist of elements specifically the same with the sublunary, or of others. If, however, that element is different from the four, how does Plato say that the whole world consists of four elements? But if it is constituted from one of the four, how does he say shortly after, that the stars consist for the most part of fire? And if the world is constituted from more elements than one, [but not from all the four] how will it happen that a divine body will not be imperfect, and how will it possess all things, through the earth, and in short the sublunary regions, have all things?
.... Such therefore being the doubts, it is better to say that all heaven consists of fire, which there predominates; but it also comprehends according to cause, the powers of the other elements, such as the solidity and the stability of earth, the conglutinating and uniting power of water, and the tenuity and a transparency of air. For as earth comprehends all things terrestrially, so the heavens comprehend all things according to fiery characteristic. So that one thing [i.e., fire] has dominion and the other elements are comprehended in it casually. It is necessary however to think, that the fire which is there, is not the same sublunary fire, but that it is divine fire, consubsistent with life, and an imitation of intellectual fire. And that the fire which is here is wholly material, generated, and corruptible. Genuine fire therefore, is in the heavens, and total fire [of the wholeness of fire] is there. But earth is there according to cause, being another species of earth, and it is fit it should, connascent with divine fire, possessing solidity alone, in the same manner as fire possesses an illuminative power. And as this celestial fire is not caustic, neither is the earth which is there gross, but the summit of each is there. (Proclus on the Timaeus of Plato, Translated by Thomas Taylor, Kessinger Books, Kila, Vol.2, pp. 420-421).

Although uncertain, the Chaldeans would naturally represent the most likely candidates for the "Barbarians" in question given their concern with synodic motion, the attested accuracy of their sidereal periods and the general high level of their astronomy. Although technically valid, the necessary inclusion of the synodic different cycles - Aether between Mercury and Venus, and planet Earth in the synodic position between the latter and Mars - would, however, clearly clash with the detailed application of the four fundamental elements, as Proclus noted. Thus his compromise is understandable, although the considerable emphasis placed on "Fire" in the above quotation still remains to be explored more fully, especially in the context of the Fifth Element.

Numerically, in terms of the Phi-Series planetary framework, the element "Aether" may be understood to be the ubiquitous value Phi ^-2 = 0.31819901 which we already know to be the "Body," "Soul" and "Spirit" of the matter as discussed lightly in the previous Section. Specifically, this exact parameter occurs firstly as the "Body" (Distance) of Mercury ("Fire"), secondly as the "Soul" (Synodic Period) between Mercury and Venus (Venus "Philosophical"), and thirdly as the "Spirit" (Velocity) of Antimony (the Jupiter-Saturn Synodic Cycle, or Saturn "Philosophical"). It is therefore apparent that this constant is a central feature of Alchemy, for it also represents "Hermaphroditic Brass", Isaac Newton's aptly named "Quintessence," and more generally, the Fifth element "Aether". As for this element's all-inclusive nature, according to the "Theurgists" quoted by Proclus in his Commentary on the Timaeus:

All things receive inclosed on ev'ry side,
In aether's wide ineffable embrace:
Then in the midst of aether placed the heav'n;
In which let earth of infinite extent,
The sea, and stars, the crown of heav'n, be fixt.
And when your power around the whole has spread
A strong coersive bond, a golden chain
Suspend from the aether.

But why should Aether - male according to its ranking as the fifth element - be considered "Hermaphroditic" in its metallic form (i.e., as Brass)? We may recall that the Pythagorean numbers 1, 2,3, 4 belonging to the first tetrad are alternatively Male and Female, whereas according to Nicomachus, the hermaphrodite: "is both Male and Female, Odd and Even" As it happens, owing to its ubiquitous nature, Phi ^-2 = 0.31819901, when added (or wedded) to the phi-series periods: 0.61800989, 1.61800989, and 2.618033989 produce numbers that are indeed both Male and Female, Odd and Even:

0.381966011 + 0.618033989 = 1 = Monad (ODD, MALE Number)
0.381966011 + 1.618033989 = 2 = Dyad (EVEN, FEMALE Number)
0.381966011 + 2.618033989 = 3 = Triad (ODD, MALE Number)

These derivations and Table 2 below are "Pythagorean" variations of Phi-relationships discussed by Dr. Ron Knott (A Formula for Obtaining Lucas Numbers), however, we will also find later that the Lucas Series is intimately related to the triangles and planes discussed in the Timaeus. Nevertheless, we can hardly consider the above to be the complete answer in our present context since it still provides no satisfactory explanation of what actually constitutes the "Odd and the Even." However, if we bear in mind that Phi ^-2 = 0.31819901 also appears to be the subject matter (i.e., the Mercury-Venus Synodic or "Venus Philosophical") in the following alchemical text: we can see that time (i.e., the Phi-Series Sidereal Periods) can indeed be "shortened" by the consistent application of exponents of Ae = Phi ^-2 = 0.31819901 and Phi, e.g., for JUPITER: Phi ⁵ - Ae ^5/2 = 11, or since Ae = Phi ^-2, Phi ⁵ - Phi ^-5 =11, etc., thus we may apply an alternating sequence to obtain an integer version of the Phi-Series periods that from unity onwards turns out to be none other than the Lucas Series:

 

Firstly, it is said in the Aesch-Mezareph that a special Decad exists with respect to alchemical "Brass", i.e., it is stated in Chapter V: "But he that will be curious, may find, that Hod has a special Decad. So also in the History of Brass, from the Law, he may easily gather a Decad," although whether what follows is the intended interpretation is another matter. In a way, this issue takes up back to Section Two and the necessary introduction of logarithmic scales to render the structure of the Solar System more comprehensible in plan view (see Section Two, Figures 1a through 1d). Here, however, we will use the period for "Brass," or "Aether" (0.38196601) as the frame of reference and take the natural logarithm of the resulting new periods, as shown in Table 3. As it turns out, the ratios of the successive logarithmic values follow a distinct sequence that includes the range 2:1 to 9:8 from Earth out to Saturn (i.e., 2/1, 3/2, 4/3, 5/4, 6/5, 7/6, 8/7, 9/8) which, although unlikely, may nevertheless be considered with respect to the instructions in Timaeus 36A to obtain "intervals of 3/2 and 4/3 and 9/8 within the original intervals"  

There is little doubt that the fractional ratios in Table 3 cause an almost unsurmountable problem, especially since Natural rather than Base-10 Logarithms are applied here, which requires an awareness of one more fundamental constant, e (2.718281828). At which point additional questions arise, not least of which is the manner by which the Phi-Series itself might have been approached in antiquity, along with the closely allied question of whether attempts were made to simplify the sequences involved. It is in this last context that we encounter "The First of Unities" which occurs in Burge's version of Timeaus the Locrian, i.e.,

But the soul of the world has (the deity) united with the centre and led outwards, investing the world wholly with it, and making a mixture of Form undivided, and of Substance divided, so as to become one mixture from these two; for which (world) he mixed up two forces, the origin of motion, one connected with the same, the other with the different: which (soul), being mixed with difficulty, was mixed not in the easiest way. Now all these proportions are combined harmonically according to numbers; which proportions he has divided according to a scale scientifically, so that a person is not ignorant of what things and by what means the soul is combined; which the deity has not ranked after the substance of the body,- for, as we say, that which is before is in great honour as regards both power and time,- but he made it older by taking the first of unities, which is 384. Now of these, the first being assumed, it is easy to reckon the double and the triple; and all the terms, together with their complements and eighths, must amount to 114695; and the divisions likewise are 114695. [The Works of Plato, George Burges, George Bell & Sons, London, 1876:150-151].

The "first of unities" is discussed further by Burges in an extensive footnote as follows:

Why this number should have been fixed upon as the first term, may perhaps be guessed at, from knowing, what is by Plutarch, De Anim. Procreat. p. 1020, C., that Plato's first term was 192, the half of 384, which was adopted by Eudorus, a disciple of Crantor; and hence too we can perhaps obtain a clue, if not the author of this treatise, at least to the time, when it was probably complied. With regard to Plato's first term of 192, Plutarch must have learnt the fact from some other source than the Timaeus itself, where there is not the most distant allusion to it; unless it be said that in his copy of that treatise there was found the identical number 192 .... Be thus. however, as it may - for Macrobius, in Somn. Scipion. ii. 2 has translated the passage as it is found at present, without any allusion to a specific number, while Stalbaum, after Boeckh, makes the first term of the series 384, without alluding even to Plutarch .... For other explanations of the reason which led to the selection of 384, as the first term of the harmonical series, the reader is referred to Boeckh's 'Philolaus,' and to Schneider's 'Disseratio de Numero Platonico,' quoted by Lindau on Timaeus p.45, who conceives with Plutarch that 384 was selected, as being the lowest number on which it was possible to operate for the eighths continually without the introduction of fractions. [Burges: 1876:151]

It would seem that "the eighths" in the last part of the above are taken to refer to the musical, or harmonic aspect as developed in detail by Abbé Batteau in a short Appendix to Burge's translation [Burges, 1876:169-173], but here as in most other treatments, the mathematical arrangements shed little light on the Solar System itself. Moreover, in the above passage only one value is given initially and a further value needs to be assumed "as regards both power and time." To this apparent end the Demiurgus "made it older by taking the first of unities, which is 384," which suggest in turn that the other number is less than this, i.e., that it has a shorter period and that the reader is required to supply it. But how should the selection proceed?
In reading ancient (and not so ancient) works, it becomes apparent that multiples of Ten - especially 1000, 10,0000 and 1,000,000 - occur in somewhat cryptic circumstances, as do the related terms "100-fold" and "1000-fold." In certain instances, e.g., when 100 and 1000 occur together this may be interpreted as a veiled reference to both the Decadic interval [1,10,100,1000] and the Harmonic Law (i.e.,100 A.U and 1,000 years) or even base-10 exponents. A more modern example of this kind of thing occurs in the Brief Guide to the Celestial Ruby by the alchemist Philalethes, in which it is baldly stated:

If that substance which Nature supplies be taken in hand by Art, dissolved, coagulated, and digested, its perfection is increased from a monadic to a denary virtue; by repeating the same process, it is increased a hundred-fold, and then a thousand-fold, etc. This wonderful Medicine penetrates each smallest part of the base metals (in the proportion of 1:1,000) and tinges them through and through with its own noble nature: your arithmetic will fail sooner than its all-prevailing power.[emphasis supplied]

while Samuel Norton in The Key of Alchemy - (Rules of Multiplication and Projection) - brackets his introductory remarks on this topic between references to Aristotle and Earth, and is almost guilty of overkill concerning the application of powers of ten in the examples cited.
But what does this have to do with the Phi-Series in general and the Phi-Series planetary framework in particular? Simply this. Commencing with the mean sidereal period of Mercury, the framework proceeds from: 0.236067978 by increasing powers of Phi to produce the additive series: 0.381966011, 0.618033989, 1.00000000, 1,618033989, 2.618033989, 4.326067978 and so on. Multiplied by 1000 and reduced to the first three places, the series becomes: 236, 382, 618, 1000, 1618, 2618, 4326, etc, since it is also additive (i.e., 236 + 382 = 618, etc.). But even so, why would the "First of Unities" be considered to be 384 and not 382, which is closer to the value for "Aether" in the Phi-Series? The answer to this question appears to be quite subtle, especially if we remember the relationship between the Phi-Series and the Fibonacci Series, namely that the limiting value for successive ratios of the latter provide the basis for the former, i.e., Phi itself. To see how this relates to the number 384 we may recall that the Phi-Series sidereal period for Mercury of 0.236067978 years is a little on the low side, which means that in our present context a more accurate estimate would be 240 using either a Babylonian value of 46/191 = 0.240837 years or a modern estimate of 0.240821 years. The 1000-fold version (240), unlike 236, 238, 241 or 242, is indeed divisible by 8, in fact both 240 and 384 are divisible by six times this number, i.e., by 48. This last part of the discussion may smack of numerology, but it far from that, i.e., since the series is additive, it may also extended in the other direction by subtraction, thus we obtain: 384 - 240 = 144, 240 -144 = 96, 144 - 96 = 48 and lastly, 96 - 48 = 48 again. The entire resulting sequence is therefore a 1000-fold representation of the Phi-Series periods, each readily divisible by 48. This yields in turn the exact Fibonacci Series, and all this from the simple base provided by two integers - 240 and the given "First of Unities" 384 - a pair of numbers that are once again in the ratio 8/5 = 1.6 as obtained from the Harmonic Mean and the initial "elements" Fire (1) and Earth (4).

Plato puts into the mouth of Timaeus a description of the formation from right-angled triangles of the figures which are the faces of the first four regular solids. The face of the cube is the square which is formed from isosceles right-angled triangles by placing four of these triangles contiguously so that the four angles are in contact at the centre. The equilateral triangle, however, which is the form of the faces of the tetrahedron, the octahedron and the icosahedron, cannot be constructed from isosceles right-angled triangles, but is constructed from a particular scalene right-angled triangle which Timaeus (54 A, B) regards as the most beautiful of all scalene right-angled triangles, namely that in which the square on one of the sides about the right angle is three times the square on the other. This is, of course, the triangle forming half of an equilateral triangle bisected by the perpendicular from one angular point on the opposite side. The Platonic Timaeus does not construct his equilateral triangle from two such triangles but from six, by placing the latter contiguously round a point so that the hypotenuses and the smaller of the sides about the right angles respectively adjoin, and all of them meet at the common centre (Timaeus 54 D, E). The probability that this exposition was Pythagorean is confirmed by the independent testimony of Proclus (pp.304-5), who attributes to the Pythagoreans the theorem that six equilateral triangles, or three hexagons, or four squares, placed contiguously with one angular point of each at a common point, will just fill up the four angles round that point, and that no other regular polygons in any number have this property....
... We are expressly told by Lucian and the scholiast to the Clouds of Aristophanes that the triple interwoven triangle, the pentagram, was used by the Pythagoreans as a symbol of recognition between members of the same school, and was called by them Health. There seems to be therefore no room for doubt that the construction of a pentagon by means of an isosceles triangle having each of its base angles double the vertical angle was due to the Pythagoreans.
The construction of this triangle depends on II.11, or the problem of dividing a straight line so that the rectangle contained by the whole and one of the parts is equal to the square on the other part. This problem of course appears again in Eucl. VI. 30 as the problem of cutting a given straight line in extreme and mean ratio, i.e., the problem of the golden section, which is no doubt "the section" referred to in the passage of the summary given by Proclus (p.67,6) which says that Eudoxus "greatly added to the number of the theorems which Plato originated regarding the section." This idea that Plato began the study of the "golden section" as a subject in itself is not in the least inconsistent with the supposition that the problem of Eucl. II.11 was solved by the Pythagoreans. The very fact that Euclid places it among other propositions which are clearly Pythagorean in origin is significant, as is also the fact that its solution is effected by "applying to a straight line a rectangle equal to a given square and exceeding by a square," while Proclus says plainly (p.419, 15) that, according to Eudemus, "the application of areas, their exceeding and their falling short, are ancient and discoveries of the Muse of the Pythagoreans." [The Thirteen Books of Euclid's Elements, Translation and Commentary by Sir Thomas Heath, Dover Publications Inc., p.98-99 ]

The connections made by Sir Thomas Heath concerning Plato, the Golden Section and Pythagorean methodology are significant, while the mention of "beauty" by both Plato and Heath is of additional interest, especially since "beauty" is often equated with the golden ratio and equiangular spirals (e.g., Huntley 1965:35,151 in a work entitled:The Divine Proportion: A Study in Mathematical Beauty). In more detail and in its entirety, the passage in the Timaeus that describes of the application of planes, triangles and solids in the above context is as follows:

Fire, water, earth, and air possessed indeed some vestiges of their own nature, but were altogether in such a condition as we should expect for anything when deity is absent from it. Such being their nature at the time when the ordering of the universe was taken in hand, the god then began by giving them a distinct configuration by means of shapes and numbers. That the god framed them with the greatest possible perfection, which they had not before, must be taken, above all, as a principle we constantly assert; what I must now attempt to explain to you is the distinct formation of each and their origin. The account will be unfamiliar; but you are schooled in those branches of learning which my explanations require, and so will follow me. In the first place, then, it is of course obvious to anyone that fire, earth, water, and air are bodies; and all body has depth. Depth, moreover, must be bounded by surface; and every surface that is rectilinear is composed of triangles. Now all triangles are derived from two, each having one right angle and the other angles acute. Of these triangles, one has on either side the half of a right angle, the division of which is determined by equal sides (the right-angled isosceles); the other hand unequal parts of a right angle allotted to unequal side (the right-angled scalene). This we assume as the first beginning of fire and other bodies, following the account which combines likelihood with necessity; the principles yet more remote than these are known to Heaven and to such men as Heaven favours. Now, the question to be determined is this: What are the most perfect bodies that can be constructed, four in number, unlike one another, but such that some can be generated out of one another by resolution? If we can hit upon the anser to this, we have the truth concerning the generation of earth and fire and of the bodies which stand in proportionals between them. For we shall concede to no one that there are visible bodies more perfect than these, each corresponding to a single type. We must do our best, then, to construct the four types of body that are most perfect and declare sufficiently for our purpose. Now, of the two triangles, the isosceles is of one type only; the scalene, of an endless number. Of this unlimited multitude we must choose the best, if we are to make a beginning on our principles. Accordingly, if anyone can tell us of a better kind that he has chosen for the construction of these bodies, his will be a victory, not of an enemy, but of a friend. For ourselves, however, we postulate as the best of these many triangles one kind, passing over all the rest; that, namely, a pair of which compose the equilateral triangle. The reason is too long a story; but if anyone should put the matter to the test and discover that it is not so, the prize is his with all good will. So much, then, for the choice of the two triangles, of which the bodies of fire and of the rest have been wrought: the one isosceles (the half-square), the other having the great side triple in square of the lesser (the half-equilateral). We must now be more precise upon a point that was not clearly enough stated earlier. It appeared as though all the four kinds could pass through one another into one another; but this appearance is delusive; for the triangles we selected give rise to four types, and whereas three are constructed out of the triangle with unequal sides, the fourth alone is constructed out of the isosceles. Hence it is not possible for all of them to pass into one another by resolution, many of the small forming a few of the greater and vice versa. But three of them can do this; for these are all composed on one triangle, and when the larger bodies are broken up several small ones will be formed of the same triangles, taking on their proper figures; and again when several of the smaller bodies are dispersed into their triangles, the total number made up by them will produce a single new figure of larger size, belonging to a single body. So much for their passing into one another. The next thing to explain is, what sort of figure each body has, and the numbers that combine to compose it. First will come the construction of the simplest figure (the pyramid). Its element is the triangle whose hypotenuse is double of the short side in length. If a pair of such triangles are put together by the diagonal and this is done three times, the diagonals and the shorter sides resting on the same point as the centre, in this way a single equilateral triangle is formed of triangles six in number. If four equilateral triangles are put together, their line angles meeting in groups of three make a single solid angle, namely [55a.] the one (180) that comes next after the most obtuse of plane angles. When four such angles are produced, the simplest solid figure is formed, whose property is to divide the whole circumference into equal and similar parts. A second body (the octahedron) is composed of the same (elementary) triangles when they are combined in a set of eight equilateral triangles, and yield a solid angle formed by four plane angles. With the production of six such solid angles the second body is complete. The third body (the icosahedron) is composed of one hundred and twenty of the elementary triangles fitted together, and of twelve solid angles, each contained by five equilateral triangular planes; and it has twenty faces which are equilateral triangles. Here one of the two elements, having generated these bodies, has done its part. But the isosceles triangle went on to generate the fourth body, being put together in sets of four, with their right angles meeting at the centre, thus forming a single equilateral quadrangle. Six such quadrangles, joined together, produced eight solid angles, each composed by a set of three plane right angles. The shape of the resulting body was cubical, having six quadrangular equilateral planes as its faces. There still remained one construction, the fifth; and god used it for the whole, making a pattern of animal figures thereon. Now if anyone, taking all these things into account, should raise the pertinent question whether the number of worlds should be called indefinite or limited, he would judge that to call them indefinite is the opinion of one who is indeed indefinite about matters on which he ought to be definitely informed. But whether it is proper to speak of them as being really one or five, he might, if he stopped short there, more reasonably feel a doubt. Our own verdict, indeed, declares the world to be by nature a single god, according to the probable account; but another, looking to other considerations, will judge differently. He however, may be dismissed. Let us next describe the figures whose formation we have now described, among fire, earth, water and air. To earth let us assign the cubical figure; for of the four kinds earth is the most immobile and the most plastic of bodies. The figure whose bases are the most stable must best answer that description; and as base, if we take the triangles we assumed at the outset, the face of the triangle with equal sides is by nature more stable than that of the triangle whose sides are unequal; and further, of the two equilateral surfaces respectively composed of the two triangles, the square is necessarily a more stable base than the triangle, both in its parts and as a whole. Accordingly we shall preserve the probability of our account, if we assign this figure to the earth; and of the remainder the least mobile to water, the most mobile to fire, and the intermediate figure to air. Again, we shall assign the smallest body to fire, the largest to water, and the intermediate to air; and again the body with the sharpest angles to fire, the next to air, and the third to water. Now, taking all these figures, the one with the fewest faces (pyramid) must be the most mobile, since it has the sharpest cutting edges and the sharpest points in every direction, and moreover the lightest, as being composed of the smallest number of similar parts; the second (octahedron) must stand second in these respects, the third (icosahedron), third. Hence, in accordance with genuine reasoning as well as probability, among the solid figures we have constructed, we may take the pyramid as the element or seed of fire; the second in order of generation (octahedron) as that of air; the third (icosahedron) as that of water Now we must think of all these bodies as so small that a single body of any one of these kinds is invisible to us because of its smallness; though when a number are aggregated the masses of them can be seen. And with regard to their numbers, their motions, and their powers in general, we must suppose that the god adjusted them in due proportion, when he had brought them in every detail to the most exact perfection permitted by Necessity willingly complying with persuasion. (Timaeus, 52D-56C, Plato's Cosmology: The Timaeus of Plato, Translated by Francis MacDonald Cornford, Bobbs-Merrill, Indianapolis, 1975:197-223, emphases supplied)

The information provided here by Plato is undoubtedly detailed and precise, although the final products remain difficult to realize. There are, it would seem, two distinct triangles that are to be utilized in the construction and there can be little argument concerning how they are to be applied or to what body and figure they pertain. Thus the first operation concerns working data that originate from an equilateral triangle subdivided by a perpendicular line from its apex. This results in a further right triangle having unity (1) for the base (B), the square root of 3 for the perpendicular height (P), 2 for the hypotenuse (H), and a slope of 60 degrees. But how might this secondary triangle to lead to the "Fire" and the "pyramid"? As we now know, the term "Fire" has diverse meanings and contexts, e.g., it is the first element, the first number (1), the first planet (Mercury), Phi-Series planetary framework values for Mercury of 0.23606798 (Mean Period/"Soul"), 0.38196601 (Mean Distance/"Body"), Phi itself - 1.618033989 - (Mean Velocity/"Spirit") and also the "Gold" that pertains to both the Sun and the "Central Fire" of the Pythagoreans. Thus we might hope (if not expect) to find that Phi is in one way or another inherent in the solution. As for arriving at the "pyramid" in our present context, in the simplest of terms, this results whenever an isosceles or equilateral triangle is made "solid," i.e., by the inclusion of the third dimension and a square base, but this in itself hardly supplies the answer that we seek. However, we may recall that we are dealing with Pythagorean concepts, the best known of which does indeed pertain to the right triangle - specifically - the square on the hypotenuse is equal to the sum of the squares on the other two sides. We also need to remember the importance assigned to growth in our present context, specifically the fifth tetrad: "Living Things: seed, growth in length, in breadth, in thickness." Thus we may consider next whether or not Plato may have provided us with the seed in the form of the given proportions belonging to the secondary triangle. But even so, how exactly are we to make this triangle grow and ultimately lead to "Fire" and the "Pyramid"?

If, as suggested earlier, the vast bulk of the writings of Plato, Aristotle and others do indeed pertain in one way or another to the matter at hand, then we may reasonably expect to find the much needed amplification further afield. And where better to commence our search than with Aristotle's own treatise On Generation and Corruption and his related discussion concerning the use of planes in the Timaeus ? Thus Aristotle explains:

For though, no doubt, Plato investigated the conditions under which things come-to-be and pass-away, he confined his inquiry to these changes; and he discussed not all coming-to-be, but only that of the elements. He asked no questions as to how flesh or bones, or any of the other similar compound things, come-to-be; nor again did he examine the conditions under which 'alteration' or growth are attributable to things. A similar criticism applies to all our predecessors with the single exception of Democritus. Not one of them penetrated below the surface or made a thorough examination of a single one of the problems. Democritus, however, does seem not only to have thought carefully about all the problems, but also to be distinguished from the outset by his method. For, as we are saying, none of the other philosophers made any definite statement about growth, except such as any amateur might have made. They said that things grow 'by the accession of like to like', but they did not proceed to explain the manner of this accession. Nor did they give any account of 'combination': and they neglected almost every single one of the remaining problems, offering no explanation, e.g. of ' action ' or ' passion ' how in physical actions one thing acts and the other undergoes action. Democritus and Leucippus, however, postulate the ' figures ', and make ' alteration ' and coming-to-be result from them. They explain coming-to-be and passing-away by their 'dissociation' and 'association', but ' alteration ' by their ' ' grouping ' and ' Position '. If the primary ' reals ' are indivisible magnitudes, are these bodies, as Democritus and Leucippus maintain? Or are they planes, as is asserted in the Timaeus? To resolve bodies into planes and no further-this, as we have also remarked elsewhere, in itself a paradox. Hence there is more to be said for the view that there are indivisible bodies. Yet even these involve much of paradox. Still, as we have said, it is possible to construct ' alteration ' and coming-to-be with them, if one ' transposes ' the same by ' turning ' and ' intercontact ', and by ' the varieties of the figures ', as Democritus does. [ Aristotle: On Generation and Corruption, Book 2, translation by H.H.Joachim, emphases supplied]

From this passage it appears that the opinions of Democritus and Leucippus were held in high esteem and accordingly given great weight. If we consider that "coming-to-be" includes both generation and time, we may also consider whether it might feasibly pertain to the problem at hand, including the Phi-Series periods and their production. From here on it is a matter of pursuit, for Plato and Aristotle appear to have provided all the materials, tools and instructions necessary. As we have already seen stated in the Timaeus (52D-56C) the triangles in question are to be "put together by the diagonal" three times with "the diagonals and the shorter sides resting on the same point as the centre." This then leads to "a single equilateral triangle formed of triangles six in number." Departing from the conventional viewpoint that the initial triangles are distributed around the centre, we may note here that the "diagonal" is obliquely alluded to in Plato's Statesman (266A-267C) - specifically the phrase "'by the diagonal and secondly by the diagonal of the diagonal." This clearly has a specialized meaning, if not application. From our present viewpoint, however, amalgamating the "alterations," "transpositions" and "turnings" alluded to by Aristotle with the "diagonal of the diagonal" located at the same point, i.e., "with the diagonals and the shorter sides resting on the same point (as the centre)" we may "transpose" and "turn" the sides with respect to the diagonal as follows:

Commencing with the secondary right triangle provided by Plato with its Base of 1 and square root of 3 for the Perpendicular, we obtain the corresponding hypotenuse of 2 from the square root of the sum of the squares of the Base and the Perpendicular (1 + 3 = 4). So far nothing has changed from what is already known, but if we now "turn" and "transpose" the initial Diagonal such that it becomes the next Perpendicular and likewise replace the initial Base value with the first Perpendicular we may compute a new value for the hypotenuse (see Table 4). Thus we obtain a new diagonal whose square is 7 and whose length is correspondingly the square root of this number. Continuing with these transpositions and turnings leads readily to the awareness that the squares on the hypotenuses follow the Lucas Series exactly from the first value (4) onwards, but this is far from the end of the matter. Although Plato's initial triangle has a slope of 60 degrees, the transpositions in question lead rapidly to a specific right triangle which has a limiting slope of 51;49,38,15 degrees (rounded at the third sexagesimal place from 51;49,38,15,09,09,..) The triangles in question obviously grow in size with each transposition, but in terms of limiting ratios we find that the "final" product is none other than a "Golden Triangle" (although neither of the two types discussed by Kappraff 1991:87) whose ratios with respect to unity (Base = 1) are the square root of Phi for the perpendicular, and Phi itself for the Hypotenuse as shown in 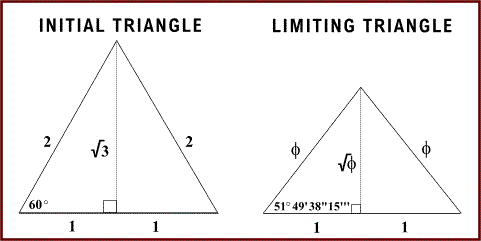Figure 6c.

Table 5. The Triangular Transpositions with the Phi and Lucas-Series

Table 5 gives the first twelve transpositions followed by the thirty-third, at which point Phi is obtained to an accuracy of fifteen decimal places. If indeed "Fire" is understood to pertain to Phi here and we also admit that we are concerned with "Divine Proportion," then we may echo those ancient "Theurgists" who proclaimed "All Things are Replete with Jove," for in this table we find that:

Plato's proportions for the initial (seed) right triangle were 1, 2 and the square root of 3. Because of this selection we find that we obtain increasingly accurate approximations for the Phi-Series Periods as we proceed. We also gain a further pair of intermediate periods between each planetary position situated on either side of the synodic - thus we possibly now embrace the two means between each pair of bodies, as described by Plato in the Timaeus. Moreover, we also obtain (from 4 onwards) the Lucas Series from the squares of successive hypotenuses. It may be remarked here that the conversion to the limiting triangle is so rapid that it is of little consequence whether the initial base-to-perpendicular ratio is one tenth or one hundred. Or, returning to the half-square, whether this ratio is one-to-one, and it is here that we may reconsider the relationships between the numbers and elements 1:"Fire", 2:"Air", 3:"Water" and 4:"Earth" stated in Timeaus 32C:

Accordingly the god set water and air between fire and earth, and made them, so far as was possible, proportional to one another, so that as fire is to air, so is air to water and as air is to water, so is water to earth, and thus he bounded together the frame of a world visible and tangible. For these reasons and from such constituents, four in number, the body of the universe was brought into being, coming into concord by means of proportion, and from these it acquired Amity, so that coming into unity with itself it became indissoluble by any other save him who bound it together. (Timaeus, 31b-32C, Trans. Cornford 1975:44; emphases supplied)

and note that the phrase: "as fire is to air, so is air to water and as air is to water, so is water to earth" also provides initial values for the sides of right triangles, i.e., 1 : 2 (Fire to Air), 2 : 3 (Air to Water) and 3 : 4 (Water to Earth) and each produce the same limiting, phi-based proportions, with the last (incidentally) commencing with the 3 : 4 : 5 Pythagorean set (for more on Pythagorean methodology and alchemy in the present context see The Rotation of the Elements by John Opsopaus). As for the significance of the phrase "so far as was possible" is concerned, the correspondence between each set becomes closer as the number of transpositions increase, with each set ultimately producing the same limiting ratios.

In the case of the "half-square" and associated one-to-one pairing, although the limiting ratios are identical, neither the Phi-Series periods nor the Lucas Series eventuate. However, from 2 onwards, the squares on successive hypotenuses generate nothing less than the Fibonacci Series, which brings us back to Timeus the Locrian: i.e.,

(Let) the half of a square, (be considered) the principle of the constitution of the Earth....For the Earth alone has the half-square, as its peculiar element; and this is the element of the (three) other substances, Fire, Air, and Water. For on the half-triangle being put together six times, there is generated from it an equilateral (solid) triangle; of which is formed the pyramid, having four faces, and their angles equal, the form of Fire, which is the most easy to be moved, and made up of the finest particles. (Burges 1876:158).

whereas it is the cube that pertains to "Earth" with respect to both the "Platonic Solids" and Pythagorean tenets. There is far more that can be said and further work to be carried out with respect to the "solids" in question, but in passing we may also recall from Section Three that in polar coordinates it is the equiangular square that provides the basis for the many facets of Spira Solaris, and this too is subject to alternation, rotation and growth.

Actually, the resulting face of the pyramid is not truly equilateral, i.e., with a base length of 2 the equal lengths of the remaining sides are obtained from either the square root of (Phi + 2) or the square root of (Phi squared +1) = the square root of 3.618033989 = 1.902113033 which results in a base-to-side difference of a little more than 5 percent. Lastly, in passing we might note here that to obtain the pyramid with this configuration we have again employed "triangles six in number," i.e., the limiting and the half-face triangles plus the four faces of the pyramid, all about a single point, the vertex.
As noted above, the slope of the hypotenuse of the transposed triangles undergoes a rapid change from the initial 60 degrees to the limiting value of 51; 49,38,15 degrees. In fact it converges so rapidly that by the second step it is already down to 52; 54,47,55 degrees followed by 51; 25,11,16 degrees at the third, and by the sixth it is 51; 51,00,25 degrees (see Table 5 and Figure 6d). As we already know, the ratios between the Hypotenuse and the Base have Phi = 1.618033989 as their limiting value, but at the third step the ratio is already 1.603567451 (approximately 8/5) and it is even closer - 1.618854427 at step six. Finally, utilizing a square base and four equal sloping sides as derived above, we obtain - applying the data from the third step, the sixth step, or the limiting slope - a pyramid with four sloping sides angled at 51; 51,00,25 degrees, 51;25,11,16 degrees, or or 51;49,38,15 degrees respectively with corresponding approximations for Phi of 1.603567451, 1.618854427 or Phi itself incorporated in the construction. This, however, may be considered an interim approach, for as Table 5 shows, most useful working values for both the slopes and Phi itself occur at steps ten and twelve with convenient slope angles of 51; 49, 40 degrees and 51; 49,38,30 degrees respectively with the closest approximation for Phi (difference 0.0002 percent) naturally obtained from the latter.

Hence they assigned everything white to the gods of heaven, and the sphere and all things spherical to the cosmos and to the sun and moon in particular, but sometimes also to fortune and to hope: and the circle and things circular to eternity, and to the motion of the heaven, and to the zones and cycles therein; and the segments of circles to the phases of the moon; pyramids and obelisks to the element of fire, and therefore to the gods of Olympus; so again the cone to the sun, and cylinder to the earth, and figures representing parts of the human body to sowing and generation. [emphasis supplied]

More pertinently, however, Proclus, in discussing those parts of Timeus the Locrian that embrace ancient Egypt, notes among other things that:

There is, then, says he, a certain region of Egypt, called Delta, about the summit of which the streams of the Nile are divided, and in which there is a province called Saïtical.

Next Proclus launches into a lengthy commentary that includes the explicit mention of a geographically defined triangle in the Nile Delta - a triangle "analogous to the one vivific fountain of all divine life, and in visible natures, to the celestial triangle which is connective of all generation" - which also, it seems, pertains to "the principle of the hypostasis of the mundane elements." After describing the methodology involved Proclus explains:

In the first place, it is worth while to observe how the narration always delivers things comprehended, proceeding from such as are more comprehensive; from Egypt, indeed, the river, from this Delta, from this the Saïtic province, and from this Saïs, sacred to Minerva. In the next place, having observed this, it will be proper to ascend through analogy of these things, to the first and most comprehensive cause of fabrication. For you may perceive this supernally comprehended by more total causes, and proceeding as far as to the last of things comprehending causes every where preceding such as are comprehended; the more total, such as are more partial; and the impartible fabrication, that which is partible, and is denominated recent; to which also the present words refer the father of the narration. And this fabrication, indeed, is filled from these causes, and particularly participates of the undefiled power of Minerva. For, in short, since we refer this war, for the sake of which the whole narration is excited, to the mundane contrariety, it will be well, proceeding in the same way, to assimilate all the knowledge of the Egyptian priests to the former [or impartible] fabrication, which stably comprehends the productive powers contained in the universe; but the history of Solon, which is always recent, and placed in mutations, to the more novel fabrication, and which administers the all-various circulations of mundane natures. We shall also be benefitted by perceiving how, in images, the difference between human and divine fabrications becomes apparent; and how, in these, Solon, indeed, calls on the priest to the development of ancient transactions, but the priest knows both such events as are reckoned ancient by the Greeks, and prior to these, such as are truly ancient. For thus also, in divine fabrications, that which is recent or junior, is converted to that which is more ancient, and is perfected by it; but the latter antecedently comprehends the causes of the former, and is established above it, by still greater and more perfect intellectual perceptions and powers. And thus much concerning the whole of the text.

It is necessary, however, to discuss every particular. With respect to Egypt therefore, some call it an image of matter; others of the whole earth, as being, divided analogously to it; and others of the intelligible, and the intelligible essence. But we say, that in what is here asserted, it is assimilated to the whole invisible order, which is the principle of visible natures. With respect to Delta also, it is produced from the Nile, being divided about the Saïtic province, so as to make its egress from one right line to the right and left, and to the sea, the sea forming the hypothenuse of the triangle, which Plato calls the Saïtic province, indicating, in what he here says, that it is that above which the stream of the Nile is divided. It is, however, analogous to the one vivific fountain of all divine life, and, in visible natures, to the celestial triangle which is connective of all generation, being proximate to the ram, which the Egyptians particularly honor, on account of Ammon having the face of a ram, and also because the ram is the principle of generation, and is moved with the greatest celerity, as being among the constellations established about the equinoctial. The mention, therefore, of Delta is here very appropriate; since the triangle, as we shall learn in what follows, is the principle of the hypostasis of the mundane elements. But the Nile is to be arranged analogous to the zodiac, as being situated under it, having an inclination similar to it, and imitating, through its divisions, the obliquity of it, and its division about the equinoctial points. The Nile also is a symbol of the life which is poured on.the whole world. Moreover, the two sides of the Nile, which run into the sea from the summit [of Delta], may be, in a certain respect assimilated to the two co-ordinations, which proceed from one root as far as to generation, and of which generation is the recipient. So that a triangle is produced from them and their common receptacle, into which they conjointly flow. But the Saïtic province, which forms a great part of Delta, participates also of a great portion of the celestial regions. Sais, therefore, must be sacerdotally referred to the constellation called the Bear, not because it is situated under it, nor on account of its coldness, but as participating of a certain peculiar efflux of the God [who presides over that constellation]. Hence likewise Saïs is not shaken by earthquakes, in consequence of receiving a firm establishment on account of the place about the pole.

Although there has been an upsurge of general research on the topic (e.g., James Q. Jacobs, Carl Monck, Frank D. Smith and Michael Lawrence Morton) the notion that "astronomical geography" is applicable to ancient Egypt is itself hardly new, given that it also occurs in alchemical analogies (e.g., Michael Maier - A Subtle Allegory) and other ancient works, including the following lament from the Asclepian Dialogue:

Are you ignorant, O Asclepius, that Egypt is the image of heaven, or, which is more true, a translation and descent of everything which is governed and exercised in heaven? And if it may be said, our land is truly the temple of the whole world. Nevertheless, because it becomes wise men to foreknow all things, it is not lawful you should be ignorant that the time will come when it may seem that the Egyptians have in vain, with a pious mind and sedulous religion, paid attention to divinity, and all their holy veneration shall become void and of no effect. For divinity shall return back from earth to heaven. Egypt shall be forsaken, and the land which was the seat of divinity shall be destitute of religion, and deprived of the presence of the Gods. [Thomas Taylor: Collected Writings on the Gods and the World ]

Here, as in previous instances the present the line of inquiry inevitably expands outwards again, and one begins to understand how Proclus came to expound at such length in his Commentary on the Timeaus, and also why Thomas Taylor in turn found it necessary to include over nine thousand "necessary emendations" in the same context. For present purposes, however, we may simply note that obscure references to "The Bear" occur in such diverse works as the Egyptian Papyrus Ani, Helena Blavatsky's Secret Doctrine (Vol 1. Bk 2, Ch.10) , Aristotle's Metaphysics (Book XIV, 6), the Aesch-Mezareph, while in The Fragments of Heraclitus (Presocratic Fragments and Testimonials) it is also stated that: "The limit of dawn and evening is the Bear; and opposite the Bear is the boundary of bright Zeus." As for the geographically defined right triangle mentioned above by Proclus, although the information is vague and coastlines can hardly be expected to remain unchanged over millennia, the simple and natural expedient of running lines due north and due west from the town of Sais (Sa al Hajar) to the present coastline (the "hypotenuse") nevertheless results (perhaps fortuitously) in a right triangle that resembles the original half-equilateral, although the slope in question is somewhat greater than 60 degrees.

The fact that this angle is slightly greater than 60 degrees, however, is nevertheless in keeping with the limiting triangle, which as we have already noted is an isosceles triangle and not an equilateral one with base angles of 51;49,38,15 degrees, which leaves an angle of 76;20,43,30 degrees at the vertex. Moreover, Proclus has already explained that:

The mention, therefore, of Delta is here very appropriate; since the triangle, as we shall learn in what follows, is the principle of the hypostasis of the mundane elements. But the Nile is to be arranged analogous to the zodiac, as being situated under it, having an inclination similar to it, and imitating, through its divisions, the obliquity of it, and its division about the equinoctial points. The Nile also is a symbol of the life which is poured on the whole world. Moreover, the two sides of the Nile, which run into the sea from the summit [of Delta], may be, in a certain respect assimilated to the two co-ordinations, which proceed from one root as far as to generation, and of which generation is the recipient. So that a triangle is produced from them and their common receptacle, into which they conjointly flow. [emphases supplied]

Assuming that the outflowing of the Nile is referred to here and there is a common point involved, then we may firstly "drop" a line from Sais to the mouth of the Delta, and secondly, attempt to fit (scaled according) either the initial or the limiting triangle. As it turns out, the best fit is in fact obtained with the former, i.e., the original "seed" triangle of Plato, but to obtain this fit and correspondence it is nevertheless necessary to rotate the axis, as shown below.

As for the ancient understanding that parts of ancient Egypt may be understood to pertain to the celestial sphere itself, this matter was a vital element in The Orion Mystery (1994) by Robert Bauval and Adrian Gilbert which related the constellation of Orion to the layout of the Giza Complex. More recently a wider celestial expansion with respect to the pyramids of Egypt and elsewhere has also been suggested by A. Kaulins (Pyramid Complexes on the Nile (Stellar Orientation). An assessment of the latter by astronomer R.C. Krupp and Kaulin's response was also carried in EGYPTNEWS Digest No.10, February 15, 1999.

Arguments have long ranged over whether the proportions of the Great Pyramid were deliberate or purely fortuitous, The pyramid's height stands in a precise pi relationship to the perimeter of the base. Pi (3.1416 ...) is the transcendental that defines the ratio between the diameter of a circle and its circumference. At the same time, pi is related to another, more interesting, irrational, phi, the so-called Golden Section. It had been observed - and ignored by Egyptologists - that not only the Great Pyramid but other pyramids as well made use of different phi relationships in their construction. Schwaller de Lubicz therefore set out to discover whether or not phi relationships were built into the Temple of Luxor. If this could be proven beyond doubt, it would corroborate these fragmentary ancient sources and force a reconsideration of the extent of ancient knowledge. If it could be shown that the Egyptians possessed advanced mathematical knowledge and scientific knowledge, it would not only prove - as many suspected - that the famous Greek intellectual flowering was but a pale and degenerate shadow of what had been known previously; it might also help substantiate the legend persisting throughout history, and widespread among the people of the world, that a great civilization had existed in the distant past even before Egypt .... For all its analytical success, science in 1937 was no closer to a solution to the mystery than in Newton's day. But a lifetime's study of mathematics - and particularly the mathematics of number, harmony and proportion - had convinced Schwaller de Lubricz that however distorted and diffuse the teachings of Pythagoras had become, in their pure form they held the key to this ultimate mystery. He was also convinced that ancient civilizations possessed this knowledge which they transmitted in the form of myth - accounting for the striking similarities of myths the world over, in cultures completely isolated from each other in space and time. Central to all these interlinked themes was that curious irrational, phi, the Golden Section. Schwaller de Lubricz believed that if ancient Egypt possessed knowledge of ultimate causes, that knowledge would be written into their temples not in explicit texts, but in harmony, proportion, myth and symbol. [emphases supplied]

Thus the idea that the constant Phi might play a fundamental role in structures such as the Great Pyramid has already been subject to serious pursuit. In addition to the above, the Phi-based slope angle is recorded in Tim G. Hunkler's Symbolism and Coincidences of the Great Pyramid and also described in detail in a wide-ranging discourse by Frank D. Smith in his appropriately named The Great Golden Pyramid (defunct link: http://galaxy.cau.edu/tsmith/Gpyr.html) which includes the configuration of the limiting triangle and the following observation:

The Great Golden Pyramid has height sqrt(PHI) = 1.272... and base 1+1 = 2. Each triangular face intersects the ground at an angle of arcsin(sqrt(PHI)/PHI), a little less than 52 degrees. Since 4/sqrt(PHI) = PI, approximately, so that the circumference of a circle whose radius is the height of the pyramid is 2 x PI x radius = 2 x PI x sqrt(PHI) = 2 x (4/sqrt(PHI)) x sqrt(PHI) = 2 x 4 = 8, and since the perimeter of the base of the pyramid is 2 + 2 + 2 + 2 = 8 , the Great Golden Pyramid approximately squares the circle.

The angle of the pyramid face to the base is, of course, the same as that derived above (51;48,38,15 degrees) while the mention of the number 8 is of interest both in the given context and historically, for as Cassidorus notes: "The number 8, which the arithmeticians call the first actual cube, has been given by the Pythagorean Philolaus the name of geometrical harmony, because he thinks he recognizes in it all the harmonic relations."

After examining in great detail the slope angles (hypotenuse) of quartz crystal , the Great Pyramid, and two right angle triangles derived from Pi and Phi, Joe resolved the "Pyrameter" triangle relative to the four faces of the Great Pyramid and the slope angle of the six triangular faces of quartz crystal: 51 degrees - 47.2 minutes + or - 3 minutes... (The three minute variation is due to the electrical sensitivity of quartz crystal)

The extremal slope values here are 51;44,12 degrees and 51;50,12 degrees respectively with 51;47,12 degrees the mean value; oddly enough, "triangles six in number" occurs here once again The sides of the "Pyrameter" triangle are scaled up and also expressed in "Lix" units, but for comparison they nevertheless reduce to a base of 1, hypotenuse of Phi = 1.61803399 and a perpendicular of 1.2732200375, the latter differing only slightly (0.094 percent) from the square root of Phi.

Objections to all such lines of inquiry (the present analysis included) must no doubt arise from the relative antiquity of the monuments in question (ca. 2700-2500 BCE) which predate Pythagoras, Plato and Aristotle by more than two millennia. On the other hand, the references to Hesiod and Homer have already moved us back to 800 BCE and there is also the Chaldean component of the matter to be considered. Moreover, if we are perfectly honest, we really cannot claim to know with absolute certainty when most of the material we have been examining originated, who originally wrote it, or even where it was written since we have been for the most part simply following what might best be termed the written Greek component. Last, but far from least, theTimaeus does indeed make early reference to ancient Egypt before proceeding with the technical details under discussion, and as we have seen above, there are further aspects to the matter in the Egyptian context. The complexities inherent in the construction of the Great Pyramid naturally give rise to all manner of possible mathematical and astronomical relationships, aided (or exacerbated) by such occurrences as the close approximation between 4/pi and the square root of Phi, (1.273239545 versus 1.272019650). Which is not to say that such relationships referred to the Pyramids are necessarily incorrect either, but rather to suggest that with an insufficient understanding of the underlying motive behind these massive monuments it is difficult to argue against objections concerning statistical probabilities, let alone what is historically possible. Nor does one need to quarrel unduly with the prevailing notion that the Egyptian Pyramids were for burial purposes, although one might nevertheless argue against the off-hand, dismissive notion that they were merely that alone in view of their great complexity and size. As for incorporating fundamental constants such as Pi and Phi into such structures, from a relatively simplistic viewpoint, what better legacy could one leave for posterity in any case?
One might suspect, however, that there was more to it that, but if neither burial purposes nor fundamental constants supply a satisfactory explanation for the amount of effort expended on these timeless monuments, then we should perhaps seek other alternatives. And it is here that we might reasonably extend the line of inquiry pursued by Schwaller de Lubricz and John Anthony West to include the Phi-Series itself and the slope values associated with the three fundamental constants for the Phi-Series planetary framework, i.e., the corresponding slope angles for Relations 5a through 5c of Section 3:

Located in South Saqqara stand the pyramids of Dhashur (Dahshur). The Red Pyramid and the Bent Pyramid are about 2 km south of the Mastaba Faraoun. The constructor of these pyramids is thought to have been Snofru (2575 - 2551 BC), who was the first ruler of the 4th Dynasty. Snofru built these two pyramids and is thought to have built the pyramid at Maidoun. His son was Cheops who continued his constructive tendencies. The Red Pyramid is thought to be older, but is inaccessible. The Bent Pyramid was built out of limestone which was quarried locally. The casing was of polished Turah limestone. This pyramid is also known as the Southern Shining Pyramid. The casing blocks are very stable and very difficult to remove because they slope inwards. The base of the pyramid is 188.6m and is 105m high. Because of the bend in construction, the original angle would have made it 128.5m high. The Bent Pyramid is unique for two reasons. The first is the angle change. There are two theories for this change. The first is that the builders may have gotten tired and wanted to reduce the volume and to finish faster. Another is that when the pyramid at Maidoun collapsed, the architect lost his nerve and changed the angle. The angle at Maidoun was 52 degrees as is the base of the Bent Pyramid. At the bend, the angle is changed to 43.5 degrees up to the peak. The second reason is that it has two entrances..

The prevailing notion is that the bend was for purely structural reasons, but against this must be weighed the fact that this pyramid retains enough of its original casing stones to suggest that engineering competency was not the primary issue. Moreover, the slope of the Red Pyramid is apparently also 44 degrees (Guardian's Dahshur), but with respect to both this value, the above 43;30 degrees and the upper slope of the Bent Pyramid of 43;21 degrees (Mark Millmore's Ancient Egypt) we may note that the limiting slope angle of 43;29,03,35 degrees would be preferred. To understand this, we need to recall that as far as the Phi-Series planetary framework is concerned, there are essentially two constants that rank above all others. The first is Relation 5a, Phi itself which is the underlying constant for the mean periods of the entire Series, i.e., the value by which the planetary mean periods increase (planet-synodic-planet). The second basic parameter is Phi to the two-thirds power (Relation 5b: 1.37824072) which is the constant by which the corresponding mean distances increase (again, planet-synodic-planet). The initial slope of 52 degrees therefore provides an approximation for Phi while the secondary slope of 43;30 degrees results in a value of 1.378598473 versus the1.37824072 of the second fundamental constant. Moreover, the former leads to the corresponding approximation of 1.618663916 for "Phi" with a slope angle of 51;50,41,21 degrees. All these various values serve to reinforce the fact that had the Egyptians wished to proceed in the simplest manner, they could far more easily have employed 45-degree slopes and equilateral sides, as a number of researchers have already pointed out (e.g., Hancock, 1993). Thus inherent in this structure we may indeed have both fundamental constants, and although the question of structural stability cannot be ignored, in this instance there nevertheless appears to be some justification for suggesting that a more technical reason for the shape of this pyramid might exist, historical ramifications notwithstanding. But then there is the slope angle of the "Pyramid at the Sun" at Teotihuacan in Mexico of 43;30 degrees (Thompson, 1987:55) which again compares favorably to the slope computed for the distance constant (43;29,03,35 degrees) and numerous other pyramids scattered world-wide might also be considered in our present context. Moreover, there appear to further numerical and calendaric considerations that apply to ancient monuments in the New World, including that at Kukulkan (see Walther Heinrich's approach to related aspects in Altamerikanische Kalender ). It may be coincidental, but major pyramids in Mexico are also stepped, in fact it could be said that many are double-stepped and double-sloped, for in addition to their obvious stepped architecture they also incorporate access steps to the summits which are less steep at the base but gradually merge with the pyramid slope towards the top, which serves to accentuate the angles of the sides, the stepped structure notwithstanding. Thus the "Temple of the Inscriptions" at Palenque employs nine steps plus a tenth flat "mastaba"-like structure at the top; the main pyramid at Chichen-Itza - famed for its serpent-like shadows just before sunset on the equinox (see Krupp 1994:299) makes use of a similar nine-step configuration, the "Pyramid of the Niches" at El Tajin employs six steps (see below) and the "Pyramid of the Sorcerer" at Uxmal, three. The immense "Pyramid of the Sun" on the other hand appears to employ five main sloping "steps" with a smaller sloping step separating the third from the fourth, and the same configuration appears to apply to the nearby "Pyramid of the Moon."

Archeologists excavating near Uruk have unearthed the oldest of all the cuneiform tablets. Those at the deepest levels and consequently from the earliest times (they are dated around 3000 B.C.) mention Inanna, Sumerian Queen of Heaven, and show a star symbol alongside the brief written text. A tablet from a slightly higher level (dated ca. 2350 B.C.) refers to the Underworld Gatekeeper as the star near the rising sun, a likely reference to occasions on which offerings were presented to Inanna in her specific guise as Venus. The special tablets in the British Museum contain mostly astronomical records and omens from the first half of the second millennium B.C.. One of them, Number 63 of the so-called series Enuma Anu enlil ("When the Gods of Air and Sky" and named after the first three words of the inscription), is devoted exclusively to the planet Venus. In one spot the text refers to the "Year of the Golden Throne," which Babylonian epigraphers attach to the reign of Ammizaduga, a fairly nondescript seventeenth-century B.C. king of the first Hittite dynasty of Babylon. The Venus Tablet of Ammizaduga has come to one of the most well studied ancient Middle Eastern documents.

Here in material from the Old Babylonian Period [1900-1600 BCE] we find (perhaps surprisingly, perhaps not) the planet Venus correctly associated with what we have understood to be the element "Air" in much later periods and different cultural contexts. As Aveni points out, the Venus Tablet has been much studied. It has also generated a number of speculative theories, but it should be recognized that very little else in the way of a technical information exists concerning the remaining planets for the period in question. Which cannot be taken as proof that they were not treated at that time, but simply that there is an absence of evidence, which (as the old adage goes) is not "evidence of absence." On the other hand, we do possess mathematical cuneiform texts which establish the high level attained by Babylonian mathematicians during this earlier period. Included here are Pythagorean sets well before the time of Pythagoras and "Newton's Method" for extracting square roots some three millennium before the time of the latter. Perhaps the best known examples of the former are to be found in Plimpton 322, where both operations are combined with the square and the half-square to obtain the former's diagonal and the latter's hypotenuse, i.e., the length of the side is multiplied by the Babylonian estimate for the square root of two (1;24,51,10 or 1.414212963., for further details see: Babylonian Mathematics and Sexagesimal Notation). Lastly, some Babylonian mathematical operations even to this day are still not fully understood, while the high level of astronomical knowledge evident in the astronomical cuneiform texts of the much later Seleucid Era [310 BCE - 74 CE] should be (to echo Proclus) "clearly evident to those who are not entirely illiterate." Lastly, the early mention of Inanna by Aveni brings to mind the three-tiered (or three-stepped) tower in Babylon and ziggurats in general, although information is increasingly vague as we push back further in time.
But in any event, more information, more accurate slope angles and further research concerning the parameters inherent in pyramidical structures seem necessary. It should be recognized, however, that applying the number of pyramid steps in distinct cultural contexts causes difficulty, especially when the cultures in question are literally oceans apart and separated by millennia. Then again, there is still the odd hint or two in the writings of the ancients to turn to for possible enlightenment. Thus remaining with the Pythagoreans and broaching the subject of the "Harmony of the Spheres" - inherent in the Doctrine of the Timeaus - we may consider the historical antecedents in terms of the Lyre and the seven planets as discussed by Burges in another of his obscure notes:

According to Boethius, De Musica, i. 20, this four-stringed lyre was invented even before the time of Orpheus. .... While Manuel Bryenus in Harmonic. i. p.362, carries the invention still higher. For he says that ' before the time of Mercury there was a four stringed lyre ... - but that Mercury, having joined two systems, formed a seven-stringed lyre;' where, as he says nothing of the other system, one may hazard a conjecture that he had heard of the tradition, mentioned by Diodorus Sic. i. 16, that the lyre was with only three strings, to answer to the three seasons. Be, however, the inventors of the four and seven-stringed lyres who they may, it is evident that the latter could not have been applied to any scientific purpose, until the three intermediate notes had been discovered requisite to make up the scale of seven notes; which were called respectively, near to, but under the highest, near to, but above the middle; and near to, but above the lowest; thus making two semitones between the middle and the highest. But instead of these semitones having the same ratio to their contiguous primary tones Pythagoras discovered that they could be represented by a string divided into two unequal parts, bearing the ratio to each other of 243 to 256 (or 3 ⁵ to 4 ⁴ ). And these seven names, invented originally for the seven strings of the lyre, were subsequently applied to the seven planets, when they were considered as giving what was called the music of the spheres. [Burges, 1876:170]

Here we encounter the "seven planets," the three-to-four separation again, plus odd references to Mercury that are followed by more Pythagorean methodology. From the primitive geocentric viewpoint the "seven planets" embrace Mercury, Venus, Mars, Jupiter and Saturn plus the two major luminaries, the Sun and the Moon. One of the major problems with this arrangement, however, is that planet Earth - even at the center - is totally excluded. Alternatively, if one wished to expand matters further but still treat Sun and Moon as "planets" there exists a more valid classification that incorporates the latter pair with all seven visible planets (Mercury, Venus, Earth, Mars, Jupiter, Saturn and Uranus) thus resulting in a total of nine. The inclusion of one more body might conclude the Decad for the Pythagoreans, but the actual awareness of a tenth object (Neptune) would at the very least require highly advanced observational techniques and optical instruments, and neither are considered likely to have been adopted in antiquity. But even this is not entirely certain, for it seems from hints and fragments that optical devices of some form or other might well have been employed in ancient times. For example, Robert Hewitt Brown, in discussing Egyptian astronomy provides information that appears to be at least partly factual and also well referenced in the later stages:

Pythagoras, who introduced the true system of the universe into Greece, received it from Oenuphis, a priest of On, in Egypt ...A knowledge of the heliocentric system, long lost, and only rediscovered by Copernicus, was not considered actually demonstrated or credited by the moderns until the rediscovery of the telescope, which revealed the phases of Venus, and so put the matter beyond doubt. We, however, are not left to conjecture only on this point, for there is some positive testimony that the ancients possessed the telescope. I quote again from Baldwin's "Prehistoric Nations." 'Much progressive in astronomy requires the telescope, or something equivalent, and it seems necessary to believe that the ancients had such aids to eyesight. Layard and others report the discovery of a lens of considerable power among the ruins of Babylon. Layard says this lens was found with two glass bowls in a chamber of ruins called Nimrod. It is plano-convex, and inch and a half in diameter, and nine tenths of an inch thick.' Sir David Brewster says, 'It was intended to be used as a lens, either for magnifying or condensing the rays of the sun' " (this settles the fact that the ancients at a very remote period were familiar with all those laws of optics a knowledge of which is required to invent the telescope, and also the manufacturing of glass. ... Mr. Baldwin in his work continues as follows: 'Even the Greeks and Romans, with lower attainments in astronomy, had aids to eyesight. They are mentioned in 'De Placitus Phil.,' lib. iii, c. v, attributed to Plutarch, also in his 'Vita Marcelli, and Pliny, 'Hist. Natur.,' lib. xxxvii, c. v, where he says that, in his time, artificers used emeralds to assist the eye, and that they were concave, the better to collect the visual rays.'... there is frequent mention of concave and convex glasses used for optical purposes, and they evidently come from Egypt and the East. Iamblicus tells us, in his life of Pythagoras, that Pythagoras sought to contrive instruments that should aid hearing as effectually as optic glasses and other contrivances aided sight. Plutarch speaks of mathematical instruments used by Archimedes 'to manifest to the eye the largeness of the Sun.' " (Brown, Stellar Theology and Masonic Astronomy, Kessinger Publications, Kila, pp. 32-33).

The alternative for knowledge that is seemingly too advanced for the cultural contexts in which it occurs, is of course, the possibility of extra-terrestrial input. In certain instances this cannot be ruled out, but at present it appears politic to proceed with caution rather than to maintain either pedantic denial or unquestioning acceptance, and this for three reasons. Firstly, it appears that an inevitable "cargo-cult" mentality might well spring up that could impede if not stultify attempts to come to terms with ourselves, our environment and our history. Secondly, it appears necessary from the start to differentiate between extra-terrestrial intelligence - an apt term strictly applicable to our own Solar System - and what might best be termed extra-stellar intelligence, i.e., from external solar systems, be they "local neighborhood" or even further afield. Other sentient life among our own small group of orbiting planets we can at least understand in terms of transportation and relatively close environments, but as far as extra-stellar intelligences are concerned, the scientific and temporal requirements necessary for space travel to this degree are almost beyond our comprehension, let alone current technical abilities, and here the impact might well be disastrous. The third reason brings us back to ancient Egypt, the time of King Djoser and Imhotep, the architect of the immense Step Pyramid at Saqqara that signified the commencement of pyramid construction on a vast scale during the Third Dynasty.

In the case of the Step Pyramid at the complex at Djoser (ca. 2700-2600 BCE) the structure is recognized as the oldest pyramid made entirely of stone, and perhaps coincidentally, it also has six steps in its final configuration. The architect responsible for this early and unusual pyramid was Imhotep, who was revered as a God by the Greeks in later times, variously described as a "Doctor, Sage, Architect, Astronomer and High Priest" and also considered by some to have been the first certifiable genius. It would appear that prior to the time of Djoser relatively nondescript rectangular "mastabas" were constructed essentially for burial purposes, thus the shift towards monumental architecture in the Third Dynasty represents a marked departure from the norm. From the layman's view at least, it seems somewhat uncertain that the prohibitive expenditure of resources and effort required to construct the Step Pyramid can be explained away in terms of the rise of centralized government, prosperity, religious beliefs, or even despotism. Moreover, the size of the complex and the extent of the construction is truly mind-boggling, both above and below the ground, the latter in particular, as Egyptologist Jaques Kinnaer explains:

The substructure of the pyramid too was built in stages and altered to compensate for the increasing size of the superstructure. It consisted basically of a great Central shaft (2) of 7 metres square and 28 metres deep, that gave access to a maze of corridors and rooms. With its more than 5.7 kilometres of shafts, tunnels, chambers and galleries, this substructure was without parallel both in size and complexity among the other Old Kingdom pyramids.

As for the more visible aspects on the surface, it is known that the structure started out as a relatively modest (if large) mastaba that subsequently underwent considerable modification, firstly enlarged upwards and outwards to a three-step configuration, and then further expanded to reach the final six-step form, all of which must have involved an enormous amount time and effort, not to mention what must have been taking place below the surface. But all to what end? Simply as a perpetual monument to the living King and the Sun? Or something else in addition? There are, it seems, a number of peculiarities that attend this massive complex, including over 400 rooms quarried out beneath the ground during an even earlier period, while numerous oddities prevail on the surface. In the compound above is a large rectangular box-shaped building - the "Divine Booth"- in addition to some large walled "buildings" that are nothing more than facades. One such wall also sports a trio of capped pillars reaching up to a shallow arc at the top, but they are attached to the wall rather than freestanding, thus they can hardly be intended to bear much weight. So perhaps they are not entirely for structural and/or religious purposes, but intended to bear information instead. There are indeed what might be called "contrarities" in Egyptian pillar construction, with columns that are either concave or convex (the present case) topped with ornate capitals that are in turn either open or closed (see Column with Closed Lotus Capital and Open Flower Capital at Karnac). Here we touch upon the related notions of "contrarity" and "simultude" that occur in later Greek writings - both necessary, as Proclus states when treating the differences between theTimaeus and Timeus the Locrian: "in order that we may know what it adds ... and in what it dissents. And that we may investigate not in a careless manner the cause of this disagreement." This injunction and line of reasoning might well apply elsewhere, especially in Egypt, e.g., the Temple of Luxor with its many opposites and peculiarities (pillar "contrarities" and inverted artwork, etc.), not to mention the sloping passages, chambers and geographical alignments of the various pyramids themselves. Moreover, additional oddities at Saqqara might merit particular attention since this complex appears to have been the starting point for the concepts embedded in the many structures that came after it. Again, it may well have functioned as a burial place, but there still seems to have been more to it than that alone. From this viewpoint a description of the Step Pyramid from TourEgypt perhaps helps set the scene for what is to follow next:

After the third stage was finished, the process to make it a true step pyramid was begun. Over 200,000 tons of stone was used to make the additional two tiers that went above the existing two-tiered structure. An additional two tiers were added above the existing four to make it into the six-tiered pyramid which is there today. A Tura limestone face was added on.
On the northern side of the pyramid, a few blocks of the casing remain. The casing blocks from the Great Pyramid rested on the individual blocks of the core masonry. The casing blocks on the step pyramid were set at an angle to take up the thrust of the successive layers.
The statue of Djoser (Zoser) that was found by excavators, was found in the Tomb Chamber. This statue was damaged but still intact. It is located in the Cairo Museum. The Tomb Chamber has a replica of the statue in this blue-tiled room. It can still be seen through the viewing slit that is at the entrance. The chamber is closed to the public. Scholars believed that the roof of the chamber could give way. The chamber walls have inscriptions that show beyond any doubt that this is indeed a burial chamber. It also contains offering rooms and most of the other features that were often found in both earlier and later tombs.
The Mortuary Temple is just north of the pyramid and is in total ruin. On the southern wall back across the Great Court from the pyramid are carved cobra heads or uraei. The cobra head is an often seen symbol in Egypt. It was once a symbol of the north. The Southern Tomb is located just outside of the southern wall. Steps lead up the wall to the other tombs and monuments outside the walls. On the left side of the stairs, there is a large hole. At the bottom of the hole, is an entrance that leads to an amazing set of chambers. This Southern Tomb is closed to the public. These chambers are also lined with the blue tiles that are found in the burial chambers in the Step Pyramid. The inscriptions found in these chambers are remarkable. They are perfectly executed and pure in line.

In the dim light of prevailing knowledge it would seem almost impossible that such concepts as the heliocentric concept could have been known this far back in time. However, if the near exact slope angles for the Period and Distance constants of the Phi-Series planetary framework are inherent in the Pyramids in ancient Egypt (and elsewhere) then it is a different matter. Moreover, if only Phi itself was embedded in the pyramids, then the case would be far weaker, but for the Phi-Series planetary framework to be of any use, it's heliocentric nature must be understood and applied, and for this the second constant is required in addition to the first. The slope angles of the Bent Pyramid loom large here, since these two key parameters are directly associated while the second constant also provides the slope angle for the much later and far removed "Pyramid of the Sun" in Mexico. This brings us back to the complex issues that arise from the adoption of "Geographical Astronomy" which effectively extends the matter globally, and indeed the distribution appears to be world-wide, with further pyramids and mounds occurring in many diverse locations, e.g., North America, Sri Lanka, and China.