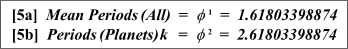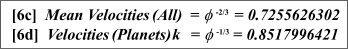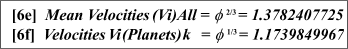PART
IVB2C: THE PHEIDIAN PLANORBIDAE
PART
IVB2C: THE PHEIDIAN PLANORBIDAE
A. TO ORDER ALL THINGS NOT ORDERED
A.1
THE PHEIDIAN PLANORBIDAE
The present paper is a
continuation of the investigation begun in
previous sections concerning the spiral form in Nature, Time, and
Place. Here, although more ancient roots undoubtedly exist the emphasis
is now concentrated primarily on the past three centuries--roughly from
the time of Carl Linnaeus (1707-1778) onward. But it is not an
historical analysis per se, nor is it a commentary on the
momentous changes that took place during this tortuous period. At least
not directly, though a darker, negative side of the matter also
surfaces as the investigation proceeds. This development itself is
perhaps surprising since it is linked to a specialized yet apparently
innocuous topic, namely the spiral formations evident in ammonites and
shells. On the other hand, however, it is not quite so surprising, or
entirely unexpected when the dynamics of the matter become
apparent.
Nevertheless, on a more positive
note the present study was precipitated somewhat fortuitously
by the format adopted by Simon Winchester for his recent best-selling
work:The Map that Changed the World: William Smith and the Birth of
Modern Geology (2001). The format followed in this publication was
explained by the latter as follows:1
CHAPTER-OPENING ILLUSTRATIONS
Incorporated in eighteen of the nineteen chapter openings
(including those of the prologue and the epilogue) will be found small
line drawings of Jurassic ammonites, long-extinct marine animals that
were so named because their coiled and chambered shells resembled
nothing so much as the horns of the ancient Egyptian ram-god, Ammon.
Soun Vannithone's drawings of these eighteen specimens are placed in
the book in what I believe to be the ammonites' exact chronological
sequence. This means that the book's first fossil, Psiloceras
planorbis, which illustrates the prologue, is
the oldest ammonite, and is to be found deepest down in any sequence of
Jurassic sediments; by the same token the final fossil, Pavlovia
pallasioides, comes from a much higher horizon, and is very much
younger. Much like the epilogue it illustrates, it was fashioned last.
It must be said, though, that anyone who flips rapidly from chapter
to chapter in the hope of seeing a speeded-up version of the
evolutionary advancement of the ammonite will be disappointed:
Ammonites floating, pulsating, slow-swimming beasts that were hugely
abundant in thc warm blue Jurassic seas do not display any conveniently
obvious changes in their Idealures, they neither become progressively
smaller with time, nor do they become larger; their shells do not
become more complex, or less. True, some ammonites with very ridged
shells do indeed evolve into smoother-shelled species over the ages,
but these same creatures then
become rougher and more ridged again as time wears on, managing thereby
to confuse and fascinate all who study them. Only studies of ammonites
from successive levels will reveal sure evidence of evolutionary
change,
and such study is too time consuming for the chance observer. Ammonites
are, however, uniformly lovely; and they inspired William Smith: two
reasons good enough, perhaps, for including them as symbols both of
Smith's remarkable prescience and geological time's amazing bounty.
However: eighteen ammonites and nineteen chapter openings? There is one
additional illustration, of
the microscopic cross-section of a typical oolitic limestone, which I
have used to mark the heading for chapter 11. Since this chapter is
very different in structure from all the others, and since much of its
narrative takes place along the outcrop of those exquisitely lovely,
honeycolored Jurassic rocks known in England as the Great Oolite and
the Inferior Oolite, it
seemed appropriate and reasonable to ask the legions of ammonites, on
just
this one occasion, to step or swim very slowly to one side.
Prologue: Psiloceras planorbis.... (Simon Winchester, The Map that
Changed the World, Harper Collins, New York, 2001: ix-x)
A fascinating set of
"Pheidian" spirals it would seem, and all carefully laid out in
planview in addition. Then there was the line of development sketched
out to feed curiosity even further--Ammon, Rams, Ramshorn Snails,
Ammonites. Yes, of course! ...but planorbis? A strange name,
but plentifully applied it would seem, and not only among ammonites
either, but ramshorn snails and the like going back to at least the
time of Linneaus (1758). And also thereafter into and beyond the early
part of the Nineteenth Century, especially Say in the former period. As
for the beautiful line drawings at the beginning of each chapter of
The Map that Changed the World, they were that indeed, and although
most were tighter spirals than Spira Solaris per se, they were
nevertheless recognizable as equiangular spirals lying within the range
already formulated and plotted in astronomical contexts, i.e., from the
inverse velocity spiral Phi 1/3
to the
planetary period spiral, Phi 2.

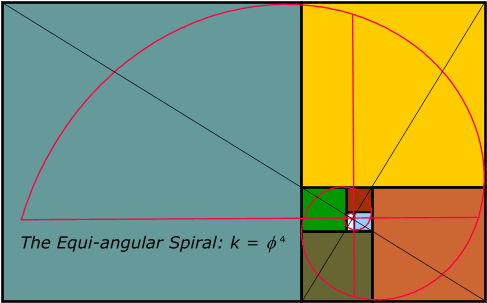
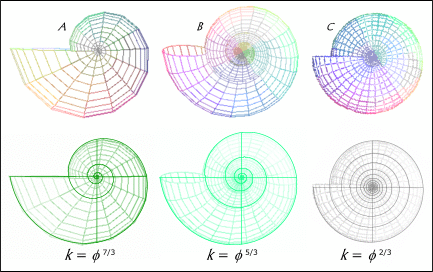
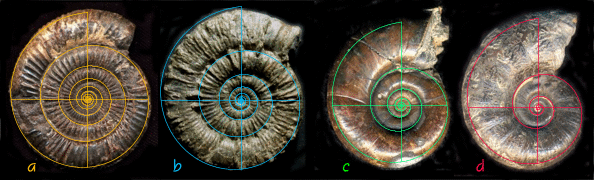
Figure
1. Spira Solaris, Growth
factor k = Phi 2
(For more on
the Capacious
Manitoba Ramshorn snail see Figure 13
below)
Thus
further Pheidian spirals with growth factors between 1.1739850
and 2.61803398874 : 1, five of which had already been
generated--two for the Periods, two for the Distances and
one for the inverse Velocity. Up to this point, however, the
emphasis had remained with the equiangular spiral based on Phi 2
in view of its all-inclusive nature on one hand and the confusion four
additional spirals might have occasioned on the other. Now there was a
practical reason for widening the range, though remnants of the
earliest ammonite, Psiloceras planorbis provided insufficient
definition to determine the fundamental spiral, at least with any
degree of certainty. This said, however, it was still apparent that
while the associated spiral in this instance was not Spira
Solaris, it was nevertheless possibly related, for the Distance
equivalent (i.e., the equiangular spiral k = Phi 4/3
with a
growth factor of 1.899547627 : 1) did in fact provide a limited
fit. Enough of an association, in fact, to give impetus to a more
detailed investigation--one that was to have a number of unexpected
results.
A.2. THE
PLANORBIDAE: FORMS
Although the assignment of the equiangular spiral k = Phi
4/3 to Psiloceras planorbis
remains
uncertain, the naming and classification of various "planorbidae"
through the Eighteenth, Nineteenth and Twentieth Centuries--especially
with respect to snails--opened up a fascinating and potentially useful
line of inquiry. The first
order of business here was obviously to conduct a survey to determine
whether or not the "planorbidae" were indeed Pheidian in the sense
stated in the
previous section ("equiangular spirals based on the constant Phi
raised
to any power, whether integer, fractional part or any number
whatsoever") and secondly, to establish whether or not the latter
possessed the
suspected relationship to Spira Solaris and associated spirals. For
this purpose the range covered by the original five spirals mentioned
earlier was extended to include further exponential "thirds" and
"sixths."
The former (in the simplest sense) being the natural continuation of
the above mentioned range k = Phi 1/3
through k = Phi 6/3 with the
insertion of the "missing" spiral k = Phi 5/3
between Phi 4/3and Phi 2;
followed by the inclusion of k = Phi 7/3,
k = Phi 8/3 and
finally, k
= Phi 9/3 for a
provisional upper
limit. Next, the intermediate "sixths" were inserted to provide a test
range that extended from k = Phi 1/6
to k = Phi 18/6
(growth
factors 1.08450588 to 4.236067978) resulting in some 18
pheidian spirals--likely more than sufficient for ammonites, though
clearly inadequate for all shells.
Here it should
be emphasized that this preliminary range
was neither haphazardly nor arbitrarily determined. It was in fact
specifically
predetermined by what might best be called the test dynamics of the
matter,
with emphasis not only on the original five Spira Solarii, but
also
on the "thirds" on either side of Spira Solaris and possibly beyond.
The
rationale behind this selection will become apparent later; as it was,
for
spirals where the growth constant k was larger than unity
standard
computations involving six revolutions with 360 data points per
revolution
were employed--thus 6 complete cycles with a total of 2160 data points
for
each equiangular spiral. Where the growth constant k was
less
than unity additional cycles were added as the growth factors
diminished.
Nevertheless, the preparation of the test set was hardly a difficult
task--the
basic mathematical elements have long been known, e.g., as
described
in detail by Sir D'Arcy Wentworth Thompson2 (On
Growth and Form, 1917,1942, 1966 and 1992); by H.E. Huntley
3 (The Divine Proportion, 1970--my own
introduction
to the topic), by Jay Kappraff 4 (Connections,
1991) and for spreadsheet users, the PHB Practical Handbook
of Spreadsheet Curves and Geometric Construction (1993) by Deane
Arganbright.5 For the present analysis,
however, each
spiral was further expanded to include two intimately related forms
locked in position and scale with respect to each other. As will be
explained later, these double forms were rigidly determined from a
fixed mathematical relationship. Thus, for example, the single
equiangular spirals for the "Spiral of Pheidias" (Schooling 1914) and
Spira Solaris were each joined by their respective additional pairs to
form associated triple sets as shown below, thus raising the
original test set to 54 pheidian spirals with more likely to be
generated on an as-required basis.
Figure 1a.
Triple
spiral configurations
for Pheidas (left) and Spira Solaris (right)
In the above, b
represents the standard format, a and c
the dual additions--the latter configuration identical to the former,
but without the cross-reference lines. Both the origin and the
technical details of these dual configurations will be supplied later,
but in passing the extended forms may appear vaguely familiar to
some readers, especially those acquainted with Sir Theodore Andrea
Cook's The Curves of Life (1914:64, 278) 6
and
Samuel Colman's Nature's Harmonic Unity (1911:115) 7.
As for their application in the present survey, their occurrence was a
continual series of surprises, for both dual formats seem to be
apparent in certain classifications, i.e., form a appears
to be a prominent feature among the more elongated Halitodae,
while c is also evident among certain shells with
smaller growth factors, the Spiral of Pheidias included. One
other point of interest (though not pursued further here) is the change
evident in c for the increase in growth factor
between Phi and Phi 2.
For the curious, the "natural" changes in form that accompany higher
powers of Phi in this configuration also provide
further room for thought, as shown below:
Figure 1b. Dual
Pheidian configurations:
k = Phi 2
to k =
Phi 16 plus k =
Phi 32
For the initial survey the
pheidian thirds and sixths were applied in a standard manner, and apart
from uniform scaling and rotation as required, the test spirals
remained unmodified throughout. Lastly, the generated data were
converted
to standard graphical formats, rendered translucent to aid scaling
and fitting, and then passed to a suitable platform for the testing
phase. The software of choice here was XARA-X,
which,
as
it turned out, was also capable of producing the output graphics and
associated
figures.
Before describing the latter a few words concerning
the initial testing phase and anticipated difficulties are perhaps
in order. It was realized from the start that it is one thing to
attempt to fit a two-dimensional spiral to drawings of
three-dimensional objects, and yet another to attempt the same
procedure with photographs,
which may or may not have been influenced by perspective effects;
optical
systems, focal lengths, depths of field, and also quite possibly
artistic licence. Some part, all, or none of which might also get
carried over to line drawings. Then there were the many problems
arising from natural
growth itself to be taken into consideration, with no truly perfect
spiral
expected to be encountered and minor departures anticipated in certain
cases. Fortunately, many ammonites possess relatively simple
symmetrical forms, i.e., spiral growth largely confined to two
dimensions without
spires or appendages extending away from the primary spiral (e.g.,
Figures 1e, 1b2, 1c, and 1d-1d3 below).
Nevertheless, the investigation--even for the relatively
flat and largely symmetrical ammonites--began with no great
expectations, but happily with a wealth of available material. And, as
it turned out, Soun Vannithone's accurate plan-view line drawings
provided both an ideal starting point and an excellent training ground;
witness:

Fig.
1e. Ammonites 69 and the Pheidian Planorbidae ( k = Phi 5/6 )
I will not go further
into the ammonite phase of the testing here except to say that overall
(in spite of the complexity of the matter and the variations
encountered)
the initial ammonite survey provided sufficient information to yield
positive answers to both the first and second questions posed. Namely,
that the spiral configurations examined could indeed be considered in
pheidian terms, and secondly, that the examples tested were also
sufficiently
relatable to the Pheidian sixths and thirds associated
with Spira Solaris
to merit the title Pheidian
planorbidae, e.g.,
Figure
1b2, k
= 6/3 = Phi 2 (c:
single, and b: dual
Spira Solaris
),61
Figure
1C: k = Phi to the 3/3, 4/3,
5/3,
6/3 powers respectively (five ammonites from: Ammonites et autres
spirales by Hervé Châtelier 61-65) and Figure 1d: k = Phi to the 3/3 power (The
Spiral
of
Pheidias), ammonite from Lower
Jurassic Ammonites
by
Christopher M. Pamplin.66 Figure
1d2: k = Phi 4/3
and Figure
1d3: k = Phi 5/3 are from Jurassic
ammonites and fossil brachiopoda 67 by
Jean-ours and Rosemarie Filippi 67.

Figure
1b2.
Ammonitesr 61
and the Dual Pheidian
configuration ( k = Phi
2)
Figure
1c. Ammonites 62-65
and the Pheidian Planorbidae
I ( k = Phi,
Phi 4/3, Phi 5/3 and Phi 2
):
Figure
1d.
Ammonites 66 and
the
Pheidian Planorbidae II (k = Phi)

Fig. 1d2. Ammonites 67 and the Pheidian Planorbidae
III ( k = Phi 4/3)

Fig. 1d3. Ammonites 68 and the Pheidian Planorbidae
IV ( k = Phi 5/3)
Thus the Phedian
Planorbidae as applied to ammonites from
an initial survey--one small inroad into a complex subject with
accompanying dynamic, temporal and historical overtones that all
appeared to merit further examination.
Next--based on
the
positive indicators gained from the ammonite phase the testing
moved on to "planorbid" snails, the treatment of which will also
be deferred until later--not because of its simplicity, but the
exact opposite--its undoubted complexity (see Figure 13 below).
Finally, from these two
bases the survey naturally turned to the more varied and extensive
range of spirals found among seashells.
A.3. PHEIDIAN
PLANORBIDAE APPLIED TO SHELLS I
Part of the third phase of the
testing is shown below in Figure 2.
Although the selection includes some better known
shells, it also omits others--primarily to emphasize certain points
in each of the selected cases.To maximise relevant information the
examples are also shown against a background plot of pheidian growth
factors along the y-axis with the corresponding equiangles of the
associated pheidian spirals along the x-axis for the successive
exponential thirds from 1 through 9. For the study (following Mosely
1838) 8 the growth factor itself was taken to
represent the
"characteristic number" (n) of the associated "primary" spiral which
was also the
parameter k.
Here the reader should be aware
that little of what is presented below is new per se, nor
is it presented as such here. Many of the assignments, although
neglected at present, were obviously known in earlier times to one
degree of accuracy or another, as the tables of related data for shells
in Thompson's On Growth and Form (1917) clearly attest
9,
e.g., the values determined by Nauman (1848, 1849),10
Muller (1850,1853)11and Macalister (1870)12.
As for the primary spiral assignments for the nine shells
shown in Figure 2, they proceed in
due order from the lowest pheidian planorbidae (k =
Phi 1/3) to the largest of
this group,
k = Phi 9/3.
Briefly, the assignments are as follows:
- Figure 2A: Cross-section of Telescopium telescopium13
(Linnaeus 1758; primary spiral: k = Phi
1/3; growth factor: 1.1739850
).
- Figure 2B: Conus princeps f. lineolatus14(Valenciennes
1832; primary spiral: k = Phi 2/3;
growth factor: 1.378240772 ).
- Figure 2C: Architectonica perspectiva15
(Perspective Sundial; Linnaeus 1758; primary spiral: k
= Phi 3/3 thus the Pheidias
Spiral ; growth factor: 1.618033989 ).
- Figure 2D: Plan view of Harpa kajiyamai16
(Rehder 1973; primary spiral: k = Phi 4/3;
growth factor: 1.899547627 ).
- Figure 2E: Pedinogyra hayii 17(Hay's
Flat-whorled Snail; Griffith & Pidgeon 1833; primary spiral: k
= Phi 5/3; growth
factor: 2.230040415
).
- Figure 2F: Planorbis corneus18(Ramshorn
Snail; Linnaeus 1758; primary spiral: k = Phi
6/3 i.e., Phi 2
thus Spira
Solaris; growth factor: 2.618034989 ).
- Figure 2G: Nautilus pompilus in cross-section19
(Chambered Nautilus; Linnaeus 1758; primary spiral: k = Phi
7/3; growth factor: 3.073532624
).
- Figure 2H: Haliotis brazieri20(Abalone;
Angas 1869; primary spiral: k = Phi 8/3;
growth factor: 3.608281187 ).
- Figure 2 I: Haliotis scalaris 21(Abalone;
Leach 1814, primary spiral: k = Phi 9/3
; growth factor: 4.236067978 ).
The
above represent a small selection from the test survey. Although
far from inclusive, the range for the shell phase of the survey
extended from the tighest spiral (k = Phi 1/12;
n = 1.040915886) out to Anadara brasiliana (Arc), k =
Phi 10 (n = 122.991869381).
Other shells
tested included Terebra, k = Phi 1/6
(n = 1.083505882); Acropora, k = Phi 1/3
(n = 1.173984997);Turritella duplicata, (after Mosely, k =
Phi 1/3; n = 1.173984997); Trochus
(varied), k = Phi 1
(n =
1.618033989) and also one or two of the better known shells, e.g., Thatcheria
Mirablis, k = Phi 7/6
(n
= 1.753149344). There were additional assignments, but to "concatenate
without abruption" (as Dr. Johnson was want to put it) would likely
disrupt the general thrust of the paper, which is not the assignment of
pheidian spiral forms to shells per se, but the dynamic,
historical, and general implications. Moreover, in so much as a full
description of the various assignments shown here should rightly follow
after the dynamics of the matter are introduced the following
descriptions are limited to a few notes concerning some of the major
points of interest. Similarly, discussion of the Haliotidae
(Abalone; excellent test subjects because of their generally flat
shapes and well-defined open spiral forms) is also deferred until later
in view of the possible relationship between this type of shell and the
complexities inherent in phi-related "whirling rectangles" (esp.
Haliotis parva; k = Phi 4
; see A4 below).

Fig. 2 The Pheidian
Planorbidae. Thirds: Growth Factors/Expansion Rates 1.174 to 4.236
Figure 2A.
Telescopium telescopium (Linnaeus 1758)
Figures 2A and 2G provide examples of the kind of fit that
can be obtained where high quality cross-sections are available, but
this is not the only reason for their inclusion here. Figure 2A
is also a miniture representation of the left vertical (Y) axis
of the figure itself, which gives the successive values of the
characteristic numbers for the nine sequential pheidian planorbidae.
Expressed in thirds, the range extends from k = Phi
1/3 out to k = Phi
9/3.
As shown in Figure 3 below, the superimposition of one half of
the pheidian spiral k = Phi 1/3reinforces
the applied scale while at the same suggesting an alternative approach
to spiral assigments. Here matters become more complex, however, for
there appears to be a three-dimensional pheidian relationship between
the widths and
heights of certain shells. So much so, in fact that it serves to aid
the assignment process, but more on this useful variation later.
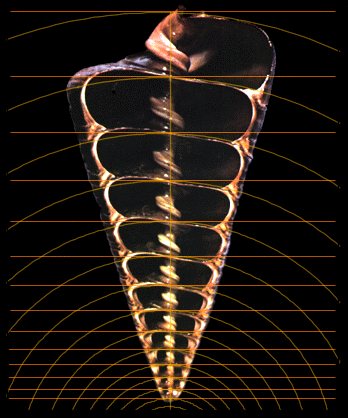 Fig. 3.
Cross-section of Telescopium
telescopium (Linnaeus 1758)
Fig. 3.
Cross-section of Telescopium
telescopium (Linnaeus 1758)
with the Pheidian Spiral and vertical scale k = Phi 1/3
Figure
2B.
Conus princeps f. lineolatus Linnaeus 175814
(above); Conus
mercator (Linnaeus
1758)23
and Conus ammiralis f.
hereditarius DA MOTTA, 198723
(below)
Were it not
for the planview of this type of shell it would difficult to assign a
spiral at all, yet as it happens--thanks to the superb collection and
presentation of Conidae
made available on the Internet by Giancarlo Paganelli (http://www.coneshell.net)
sufficient examples exist to assign the primary spiral k =
Phi 2/3 (growth factor: 1.378240772
)
with a fair degree of confidence. Although Conus tulipa
24 is an exception (at least from the test
perspective;
primary spiral: k = Phi 5/3)
further examples show a number of intriguing variations, including
possibly related scaling and multi-dimensional effects, varying from
pronounced single line (e.g., Conus
doreensis), double line (Conus
mercator; Figure 4) and
multiple spiral markings (Conus
ammarilis; Figure 4b and Conus
planorbis; Figure 4c). A more diffuse but similar example is Conus
bandanus). Here the scale of the spiral applied in the vertical
plane to the front of the shell is unchanged from that used for the
planview. On the right (rear), still fixed with respect to the tip of
the
spire, the scale is increased until the outer whorl meets the same
spiral markings that unwind on the other side of the shell. Similar
test procedures involving 1, 2 and 3-whorl extensions are helpful
in the case of more elongated Conidae, e.g, as applied
in Figure 4b (a single whorl extension applied to Conus
ammiralis). Though pertinent to the survey, the well defined "pheidian"
markings
on the three examples below are perhaps unusual; nevertheless the same
basic technique remains applicable to other Conidae with
more diffuse patterns, if not greater complexity.

Fig.4.
Conus Mercator
Linnaeus 1758. Single spiral, k = Phi
2/3
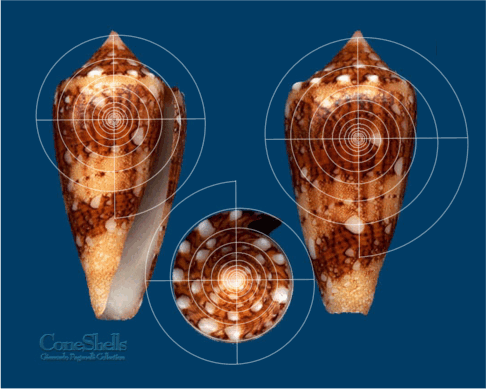 Fig.4b. Conus ammiralis
f.
hereditarius DA MOTTA, 1987. Single
spiral, 1-whorl extension; k = Phi 2/3
Fig.4b. Conus ammiralis
f.
hereditarius DA MOTTA, 1987. Single
spiral, 1-whorl extension; k = Phi 2/3

Fig.4c. Conus planorbis
f.
vitulinus HWASS in BRUGUIÈRE, 1794. Single
spiral; k = Phi 2/3
Figure 2C. Architectonica
perspectiva (Linnaeus
1758) and Similar Shells
Figure 2C is shown in inverted planview
for two major reasons. Firstly, a trio of like shells graced
the dust cover of the 1942 edition of Sir D'Arcy Wentworth's
On Growth and Form in this exact representation. The
reason seems clear enough from the inverted "perspective" of the
associated spiral (see Figure 5 below; perhaps the latter was also
influenced by Aristotle, if not the three-fold number--"Said
Aristotle, prince of philosophers and never-failing friend of truth:
All things are three"). Here, one should also note that
the "ratio of breadth of consecutive whorls" in Thompson's tabular data
for shells of this general type,
i.e., Solarium trochleare is given as 1.62 25,
thus the Golden Section to two decimal places. The degree of accuracy
is low, but hardly conclusive proof that a better value was not known.
In fact there is very good reason (as explained in detail below) to
believe that both Canon Mosely and Sir D'Arcy Wenthworth Thompson were
intimately acquainted with the not only the Phedian planorbidae per
se, but also the dynamics of the matter.
In the meantime, Figure 5 below emphasizes not only the distinct
markings and underside perspective view, but also the fit in standard
and open double form with respect to the top
markings of the shell.

Fig.5.
The
underside and top of Architectonica perspectiva;
Single spiral (B and C); open double spiral (A); each k = Phi
1
Many shells
with this assignment appear to be "golden" in more ways than one (see
Figure 6 below), adding further merit to the observation attributed to
Aristotle and Ovid30 in the last section,
i.e.,
Said Aristotle, prince of
philosophers and never-failing friend of truth : .........
All things are three; The
three-fold number is present in all things whatsoever.
Nor did we ourselves discover
this number, but rather natures teaches it to us...
Fig.
6.
Liguus virgineus (Linnaeus, 1758)31
Fixed
Inset scale, 1-whorl extension; k = Phi 1
Figure 2D. Harpa
kajiyamai (Rehder 1973) above; Harpa goodwini (below)
The assignment of the primary spiral remains uncertain for Harpidae
due to the small number tested to date.
Nevertheless, the initial assignment (in spite the latter) would
appear to be the pheidian spiral k = Phi
4/3
(growth factor: 1.899547627). The example of Harpa
goodwini shown below (Defunct source: Guido T. Poppe,26
Conchology
http://www.conchology.uunethost.be/
) shows the planview fit (top and underside views) for the single
spiral in question; as in the case of other intriguing examples (e.g.,
Haliotidae and Conidae) one could no doubt spend a long
time working to decode the complex formations also evident here.
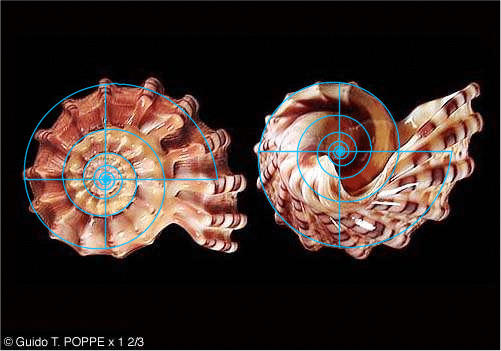
Fig. 7. Harpa
goodwini (Top and underside) with the single Pheidian Spiral
k = Phi 4/3
Figure 2H. Haliotis brazeri (Angus, 1869);
unridged variant below
Unlike the double spiral applied to the ridged form of Haliotis brazeri in Figure 2H, the single spiral applied to the smoother variant below 20a follows the central ridge, but in
both cases the
primary pheidian spiral nevertheless appears to be k = Phi 8/3. D. L. Beechey (source: http://seashellsofnsw.org.au/Haliotidae/Pages/haliotis_brazieri.htm)
notes that: "There is continuing debate on whether the smooth form and the
spirally ridged form are separate species, or forms of the one variable
species. Intergrades between the two shell forms exist (although
uncommon), supporting the view that there is only one variable species.
Until anatomical studies are done the issue remains unresolved."
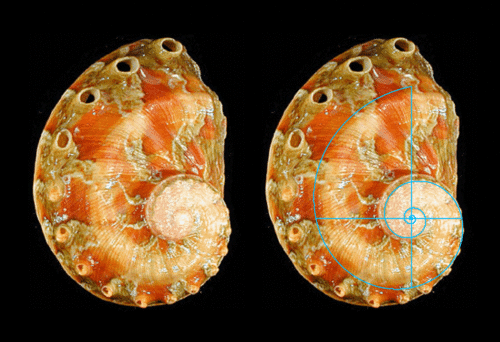
Fig.
7b. Haliotis brazeri with the single
Pheidian Spiral
k = Phi 8/3
Figure 2E. Hay's
Flat-whorled Snail
The availability of accurate planviews of the top and the undersides of
certain shells is obviously helpful in assigning the primary spiral,
but there are still additional complications
where pronounced curvature is present. For the examples selected,
however, a useful modifying effect became apparent during the survey,
namely what might be called "pheidian three-dimension growth" for
lack of a better term. For example, the double spiral configuration
applied to Hay's Flat-whorled snail is not only applicable to the
underside, but to some extent it also follows the curvature of the
shell
along the top, as in Figure 2 and also below, where it not only
fits the flatter interior around the low spire, but also generally
corresponds to the linear markings of the shell between the inner
and outer spirals further out:

Fig. 8. Hay's
Flat-whorled Snail17 and the Double
Spiral k = Phi
5/3
Figure 2G. Nautilus
pompilus (Linnaeus 1758)
Shown above in Figure 2G, Nautilus pompilus was
assigned the primary spiral and characteristic number of
k = Phi 7/3 and
n =
3.073532624 respectively, which is hardly new. Nor is it a particularly
difficult assignment. In fact Sir D'Arcy Wentworth Thompson, having
provided the value 3.00 for the characteristic number of
this shell in his tables preferred to devote his attention to more
difficult problems, concluding that "The numerical ratio in the case
of the Nautilus happens to be one of unusual simplicity." 22
As indeed it is, at least in comparison to many other types of
shells.
Shown below is an enlarged version of the same cross-section of the
Nautilus, but this time with the double primary spiral k =
Phi 7/3. Here, as in other
examples, the
relationship between the two spirals remains fixed irrespective of
scaling. Thus, although the outermost part of this variant shows some
departure from the shell
itself (i.e., at the bottom), the inner spiral (unaltered in position
from its original form, scaled in situ and locked with respect
to the outer) still follows the internal syphon tube, though departing
slightly from it over the final three chambers.

Fig.
9. Cross-section
of Nautilus pompilus (Linnaeus 1758); Double Spiral k =
Phi 7/3
Figure 2F. Planorbis
corneus (Linneaus 1758)
The Planorbidae were one of the main targets in the survey--not
only because of a particular interest in their classification, but also
for technical reasons amply demonstrated by the the standardized,
technical photographs in Arthur H. Clarke's The Freshwater Molluscs
of Canada (1981:175).27 The latter work
included the "Superfamily
Planorbacea, FAMILY
PLANORBIDAE (Ramshorn Snails)" described in part as "Shells
small to moderately large, dextral or sinistral, flatly coiled in
most species and with a very low spire" 28
--the latter point clearly useful for testing. As for further general
details of the Family Planorbidae, Martin Kohl (Defunct link;
originally at Freshwater
Molluscan Shells: Planorbidae;
http://members.aol.com/mkohl2/Planorbidae.html ) provides the following:29
Generally
referred to as "Wheel Snails", "Orb Snails", or "Ramshorn snails", the Planorbidae
are the largest family of aquatic pulmonate gastropods, with species
present on all continents and most islands. They are sinistral in their
orientation, in spite of the fact that some may appear dextral due to
the spire being sunken more than the umbilicus. Many of these species
harbor the larvae of parasitic worms, particularly southern and
Old-World taxa. Banarescu (1990) provides the following classification,
here tabulated. Many subgeneric and subspecific names are in use, so
for instance, the first specimens pictured are Planorbella
(Pierosoma) trivolvis trivolvis (Say, 1817). [Martin Kohl;
planorbidae.html ]
The example of Planorbis
Corneus
used in Figure 2 is from the above source; the parent
photograph is
shown below as Figure 10. Many members of this family appear to be pheidian
in one form or another, and like Architectonica, Trochus,
etc.,
many seem to be "golden" in addition--a worthy subject in its own
right,
though it will not be pursued further in the present survey.
Fig.
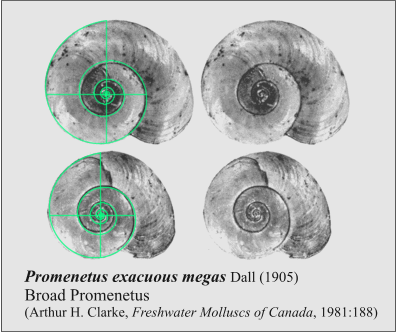
10. Planorbis Corneus (Ramshorn snail; Linnaeus 1758)18
and
Spira Solaris ( k = Phi 2)
Returning
to Planorbis
Corneus, the partial fitting (as opposed to the whole
outline)
of the Pheidian spiral k = Phi 2
is shown
here for
a number of reasons. Firstly, although certain planorbidae
appear
to show little or no discernable changes in the primary spiral e.g., Promenetus
exacuous megas, Dall 1905, primary spiral: k = Phi
5/3
Fig.
11. Broad Promenetus Ramshorn snails with single
spiral: k = Phi 5/3
in others the visible inner
regions differ from the general outline
beyond that asssociated with curvature effects and the natural
overlapping of the tube. Moreover (as seen in Figure 10 above), further
differences are also evident depending on which side of the shell is
under consideration. Finally, though another increase in complexity, in
some cases the double spiral configuration is also apparent, i.e., with
respect to ridge formations, as in the case of the Great Carinate
Ramshorn and Capacious Manitoba Ramshorn snails:
Fig.
12. Great Carinate Ramshorn snail with double
spiral: k = Phi 2
Although beyond the original
intent of the survey, investigation of the
apparent changes from the initial (inner) spiral k = Phi
2 for the Capacious Manitoba
Ramshorn snail
suggest that the relatively abrupt shifts may be interpreted as downward
changes, i.e., from the initial spiral k = Phi 2
through k = Phi 11/6
to
k = Phi 5/3 (or
expressed in sixths for
"continuity", from k = Phi 12/6
through k = Phi 11/6
to k =
Phi 10/6) as shown below:
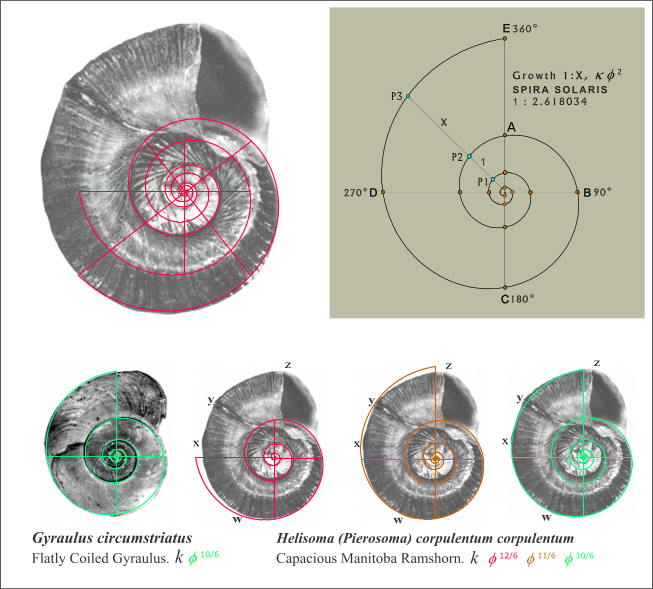
Fig.
13.
Capacious Manitoba Ramshorn snail with double and single
spirals:
k =
Phi 12/6, k =
Phi 11/6 and k
= Phi 10/6.
In Figure
13 the
double spirals (though still applicable) are omitted for clarity in all
but the primary assignment. The other assignments remain provisional
owing to the small sample tested. As for the whys and the wherefors of
the matter, here it it necessary for a brief revision of the
astronomical side of the Pheidian planorbidae before moving on
to a description of the generation of the double spiral itself.
A4. THE
PHI-SERIES AND THE SOLAR SYSTEM REVISITED
A4.1 EXPONENTIAL CONSTANTS
Up to the mid-point of
Section III representations of the Solar System
were largely logarithmic, two-dimensional in form, and also generally
static in nature, despite discussions concerning periods of revolution,
lap cycles, planetary orbits and varying
velocities. Yet the complexity of the Solar System, its endless and
varying motions, its waxings and wanings, its growth and decay, its
anomalies and its regularities all suggest it is something far more
than a mechanical clock or indeed anything that simplistic. But at
least
from the analyses presented in Section III there appears to be some
justification
for suggesting that an exponential component exists in the structure
of the Solar System, and moreover, that remnants of it remain in the
two log-linear zones and the three inverse-velocity relationships
discussed in earlier sections. But where does this leave us? According
to the
methodology applied to the mean periods of revolution and the
intervening synodic periods, the log-linearity in the Solar System
largely translates into variants of the Phi-Series such that the mean
periods (Sidereal
and Synodic) increase sequentially by successive powers of Phi while
the mean periods of the planets alone increase by Phi squared, i.e.,
relations 5a and 5b:
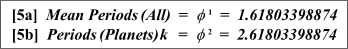
Relations
5a
and 5b. The Fundamental Period Constants
Correspondingly,
because of the the third law of planetary motion and the relationship
between the mean periods, mean distances and mean velocities, the
factor Phi 4/3 (1.899547627)
generates the mean planetary distances while the square root of
the latter generates the mean distances throughout, i.e., including
intermediate the synodic positions, thus:

Relations
6a
and 6b. The Fundamental Distance Constants
Moreover,
and in like manner, while the mean periods and mean distances increase
with each successive revolution, the all-inclusive mean velocities and
planetary mean velocities correspondingly decrease by Phi to the minus two-thirds and
phi to the minus one-third respectively, i.e., the velocity constants
are:
Relations
6c
and 6d. The Fundamental Velocity Constants
Lastly, such
is the nature of the equiangular spirals under consideration that the
inverse and normal spirals are virtually identical to each other (with
minor reservations, i.e., the matters of phase and origin referred to
in the previous section). Nevertheless, apart from the latter
points, equiangular spirals based on relations 6e and 6d are (for
present practical purposes) interchangeable with those based on the
diminishing velocities of relations 6c and 6d.
Relations
6e
and 6f. The Inverse Velocity Constants
By now the reader has no
doubt already recognized that six of the equiangular spirals based on
the constants in relations 5a, 5b, 6a, 6b, 6e and 6d are those applied
above to Ammonites, Land, and Sea shells. These six spirals also
represent the majority of the Pheidan planorbidae shown in
Figure 2, and for the range in question, i.e., from the inverse velocity
spiral Phi 1/3
out as far as
Phi
3, only Phi 5/3
is missing
below Spira Solaris, while the remainder extend sequentially
beyond the latter, i.e., Phi 7/3,
Phi 8/3 and Phi 9/3.
But what do velocities have to do with the present discussion
concerning the spiral formation evident in shells? Here it is perhaps
helpful to give Sir D'Arcy Wentworth Thompson's description of this
aspect in On Growth and Form: (1917) where it is included in
the
latter's detailed description of the equiangular spiral: 35
Of the
spiral forms which we have now mentioned, every one (with the single
exception of the cordate outline of the leaf) is an example of
the remarkable curve known as the equiangular or logarithmic spiral.
But before we enter upon the mathematics of the equiangular
spiral, let us carefully observe that the whole of the organic
forms in which it is clearly and permanently exhibited, however
different they may be from one another in outward appearance, in nature
and in origin, nevertheless all belong, in a certain sense, to one
particular class of conformations. In the great majority of cases, when
we consider an organism in part or whole, when we look (for instance)
at our own hand or foot, or contemplate an insect or a worm, we have no
reason (or very little) to consider one part of the existing structure
as older than another; through and through, the newer particles have
been merged and cornmingled among the old; the outline, such as it is,
is due to forces which for the most part are still at work to shape it,
and which in shaping it have shaped it as a whole. But the horn, or the
snail-shell is curiously different;
for in these the presently existing structure is, so to speak, partly
old
and partly new. It has been conformed by successive and continuous
increments; and each successive stage of growth, starting from the
origin, remains
as an integral and unchanging portion of the growing structure.
We may go further, and see that horn and shell,
though they belong to the living, are in no sense alive. They are
by-products of the animal; they consist of " formed material," as it is
sometimes called; their growth is not of their own doing, but comes of
living cells beneath them or around. The
many structures which display the logarithmic spiral increase, or
accumulate, rather than grow. The shell of nautilus or snail, the
chambered
shell of a foraminifer, the elephant's tusk, the beaver's tooth, the
cat's claws or the canary-bird's–all these shew the same simple and
very beautiful spiral curve. And all alike consist of stuff secreted or
deposited by living cells; all grow, as an edifice grows, by accretion
of accumulated material; and in all alike consist of stuff secreted or
deposited by living cells; all grow, as an edifice grows, by accretion
of accumulated material; and in all alike the parts once formed remain
in being and are thenceforward incapable of change.
In a slightly different, but closely cognate way,
the same is true of the spirally arranged florets of the
sunflower. For here again we are regarding serially arranged
portions of a composite structure which portions, similar to one
another in form, differ in age; and differ also in magnitude in
the strict ratio of their age. Somehow or other, in the
equiangular spiral the time-element always enters in; and to
this important fact, full of curious biological as well as mathematical
significance, we shall afterwards return.
In the elementary mathematics of a spiral, we speak
of the point of origin as the pole (O); a straight line having
its extremity in the pole, and revolving about it, is called the radius
vector; and point (P), travelling along the radius vector under
definite conditions of velocity, will then describe our spiral curve.
Of several mathematical curves whose form and
development may be so conceived, the two most important (and the only
two, with which we need deal) are those which are known as (1) the
equable spiral, or spiral of Archimedes, and (2) the equiangular or
logarithmic spiral.
The former may be roughly illustrated by the way a
sailor coils a rope upon the deck; as the rope is of uniform thickness,
so in the whole spiral coil is each whorl
of the same breadth as that which precedes and as that which follows
it. Using its ancient definition, we may define it by saying, that
"If a straight line revolve uniformly about its extremity, a point
which likewise travels uniformly along it will describe the equable
spiral*." Or, putting the same thing into our more modern words, "If,
while the radius vector revolve uniformly about the pole, a point (P)
travel with uniform velocity along it, the curve described will be that
called the equable spiral, or spiral of Archimedes." It is plain that
the spiral of Archimedes may be compared, but again roughly, to a
cylinder
coiled up. It is plain also that a radius (r = OP),
made
up of the successive and equal whorls, will increase in arithmetical
progression: and will equal a certain constant quantity (a)
multiplied by the whole number of whorls, (or more strictly speaking)
multiplied
by the whole angle (θ) through which it has revolved: so that r =
aθ. And it is also plain that the radius meets the curve (or
its tangent) at an angle which changes slowly but continuously, and
which
tends towards a right angle as the whorls increase in number and become
more and more nearly circular.
But, in contrast to this, in the equiangular spiral
of the Nautilus or the snail-shell or Globigerina, the
whorls continually increase in breadth, and do so in a steady and
unchanging ratio. Our definition is as follows: "If, instead of
travelling with a uniform velocity, our point move along the
radius vector with a velocity increasing as its distance from the
pole, then the path described is called an equiangular spiral."
Each whorl which the radius vector intersects will be broader than its
predecessor in a definite ratio; the radius vector will increase in
length in geometrical progression, as it sweeps through successive
equal angles; and the equation to the
spiral will be r = aø. (Sir D'Arcy Wentworth Thompson, On
Growth and Form, 1917, 1942,1992:751-753; diagrams and
footnotes omitted; the emphases are Thompson's alone)
Thus time and
velocity, and both intimately associated.
Where next? Since time
and motion are clearly involved, the matter of the "whirling
rectangles" and the formation of the double spiral.
A4.2.
WHIRLING RECTANGLES, SQUARES, AND EQUIANGULAR SPIRALS
In some respects the subject of "Whirling" rectangles represents a
modern two-part puzzle--not so much the topic per se as the
apparent stagnation and lack of understanding that (for whatever
reason) currently attends it. This rectangle--"Golden" in the sense
that the ratio between the length and the width is 1.61803398874
: 1 (i.e., Phi : 1 )--is more often than
not shown in association with the side view of Nautilus pompilus,
which is the first part of the puzzle, since the spiral
assignment for Nautilus has long been known and the spiral
in question has a growth factor (or expansion rate) more than twice
that of the
latter. The second part of the puzzle concerns why the matter is rarely
taken further. It is surely a natural step when a spiral is shown in
relation to a rectangle with attendant squares, etc., to investigate
the details and if possible determine what lies behind the observed
effect. By way of explanation, maintaining the same ratio between
rectangle and square throughout, the original rectangle may be
successively
partitioned into firstly a square with both sides equal to the previous
width, and secondly, into another similar golden rectangle, and so on,
rotating 90 degrees with each successive partition. As it so happens,
the combination of the quarter-perimeters inscribed in the resulting
squares closely approximate an equiangular spiral, as is often
demonstrated in discussions concerning this topic, though the spiral
itself (actually
k = Phi 4) is rarely
identified (at least this was the case when I first mentioned it!). Nor
is
the
representation a true spiral, as most commentators point out, though
few tend to elaborate much further. An exception is Jay Hambidge,36
who also describes a similar (though not identical) treatment of
"Whirling Rectangles" with respect to root-5 rectangles in Dynamic
Symmetry,
(1920).
Fig.14.
"Golden Rectangles," Squares, and the Equiangular Spiral k = Phi 4
As for the "Golden
Rectangle" and the observed spiralling effect, it is perhaps useful to
remain with the astronomical side of the matter for a while and
consider again what was stated in Section IV (Spira Solaris
Archytas-Mirabilis), i.e.,
With respect to the
present astronomical application and the exponential planetary
framework it may be noted that all mean periods (planet-synodic-planet)
increase by phi itself while all planetary periods per
se increase by phi squared. Therefore the required period
function should increase by the square root of phi per
90-degree segment and by phi squared per
revolution. Thus for explanatory purposes, commencing with unity, the
first 90-degree segment would have the value 1.27201965, the second
(the half-cycle, or 180 degrees) 1.618033989 (phi itself), the third
2.058171027, and at the full cycle, phi squared =
2.618033989.
Not that this is new,
though the above application is somewhat specialized. In fact Jay
Kappraff 37shows quadrantal growth for the
equiangular
spiral in this exact manner in a schematic diagram of the logarithmic
spiral, replete with attendant rotating and expanding rectangles
(Figure 2.11,1991:46). Here it may be noted that in general terms the
fixed increase per quadrant is the fourth root of the growth
factor per revolution, as Sir D'Arcy Wentworth Thompson38 was obviously aware in citing the
square root for the half-cycle and the square root again for the
quarter (see also Figure 15c below). The fourth root in this
context applies to all pheidian spirals and as such it is also inherent
in the "Golden Rectangle," though this may not be immediately apparent
for a number of reasons. Firstly, the associated spiral is in a sense
incomplete with respect to the full rectangle and largest square,
whereas it is always "complete" with respect to the smaller rectangles,
etc.(see Figure 14 above). Secondly, quadrantal growth in this
application is more naturally understood with respect to what may be
termed the "outer" spiral as opposed to that enclosed by the rectangle
itself. Thirdly, though
identical in form, in addition to being external the outer spirals are
also inclined at specific angles to both the rectangle and the inner
spiral.
This should become more apparent from Figure 15, which incorporates the
above data for Spira Solaris and in addition shows the orientation of
the
double
spirals to the parent rectangle:
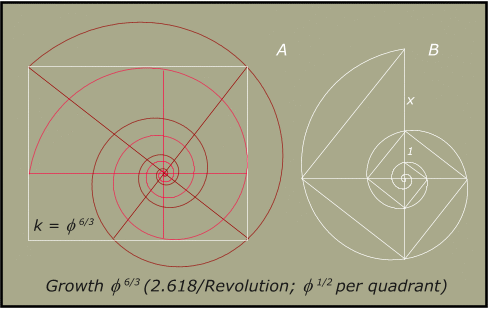
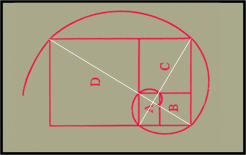
Fig.
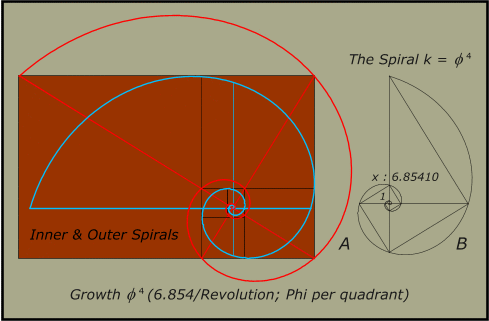
15. Rectangle with Inner and outer Spirals for Spira Solaris, k =
Phi 2
Thus while Figure 15 is a
representation of quadrantal growth that results in an increase of Phi
2 per revolution, the same
delineation is also traced
out by both the inner and outer spirals associated with the rectangle.
However, it is the outer spiral that shows the fourth root
increases more clearly, and both are perhaps best demonstrated by
animated
graphics, firstly with respect to the original "Golden" rectangle and
the spiral k = Phi 4 and
secondly with
respect
to the associated quadrantal radii vectores for the same spiral; see
Quarteranimation I
(60kb) and Quarteranimation
II (117kb) respectively.
As for the "Golden Rectangle" in
this particular context, one of its main values would appear to
be that it provides a natural lead-in to the above because of the close
fit between the quarter-circumferences and the spiral k = Phi
4.
Fig.
15b. The Golden Rectangle with Inner and outer Spirals for k = Phi
4
Fig.
15c.
The Golden Rectangle
and the Outer Spiral by Sir D'Arcy Wentworth Thompson
(On Growth and Form, Chap. XI, The Equiangular Spiral,
"Concerning Gnonoms," Fig.356; rotated, diagonals added)
But as the animations
show, it
is neither the rectangles nor the squares that are rotating, but the
effects of spiral growth that the latter approximates so well in this
particular example. Once the concept is understood, however, it may be
extended to any and all pheidian spirals, which was in fact how the
double spirals shown in Figures 1a and 1b were initially generated. It
is at this juncture that the assignment of primary spirals to Haliotidae
may be resumed.
HALIOTIDAE
Figure 2H: Haliotis brazieri ( Angas 1869).Figure
2I: Haliotis scalaris ( Leach
1814). Below: Haliotis parva (Linnaeus
1758 ).
The two examples from this group shown in Figure 2 have growth
factors considerably smaller than that discussed with respect to the
Golden Rectangle (i.e., k = Phi 8/3
and k = Phi 9/3
respectively). Nevertheless, the spiral assignments for Haliotidae
extend far higher and within this group it would appear that the
primary spiral k = Phi 4
is
applicable to Haliotis parva:
Fig.
16. The "Golden Rectangle", Haliotis Parva 39
and single spiral: k = Phi 4
Here the
flatter underside of the shell supplies additional reference markings.
Neither the top, or the underside, or indeed the spires are truly flat,
though the latter are relatively low in some cases and only slightly
raised in others. Thus although well suited for the kind of testing
carried out here there are nevertheless spatial complications to be
taken into consideration. Then again, the Halitiotidae also seem
to incorporate the double spiral form, especially in the higher
assignments as seen in Figure 2 and the three examples of Haliotis
parva 39
shown below in Figure 17a (topview) and 17b (underside).
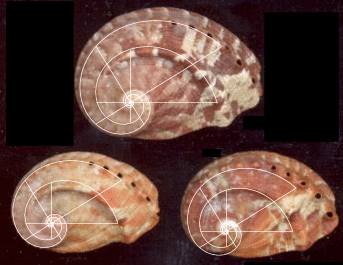
Fig.
17a. Haliotis
Parva (topview) with the Double Spiral k = Phi 4
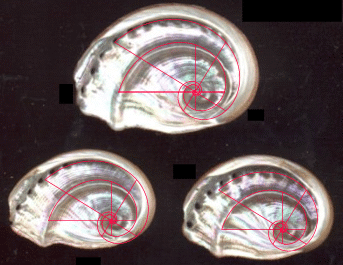
Fig.
17b. The
Underside of Haliotis Parva with the Double Spiral k = Phi 4
Subject to revision and
possible extensions, provisional assignments from the initial survey
for some of the other Haliotidae are as follows:
- Haliotis assimilis, k = Phi 8/3
(n = 3.608281187);
- Haliotis ruber, k = Phi 8/3
(n = 3.608281187)
- Haliotis queketti, k = Phi 9/3
(n = 4.236067978 )
- Haliotis thailandis, k = Phi 9/3
(n = 4.236067978)
- Haliotis roie, k = Phi 9/3
(n = 4.236067978)
- Haliotis Parva, k = Phi 4
(n = 6.854101966)
- Haliotis crebisculpta, k = Phi 5
(n = 11.090169944)
- Haliotis semiplicata, k = Phi 5
(n = 11.090169944)
- Haliotis elegans, possibly k = Phi 10-12
(n = 321.996894).
For additional information
on Haliotidae (and other shells) see the related sections in
the following short list (in alphabetical order):
- Conchology (Guido T. Poppe; defunct link:
http://www.conchology.uunethost.be/
)
- Hardy's Internet Guide to Marine Gastropods (Eddie
Hardy; http://www.gastropods.com
)
- ManandMolluscs.net (Avril Bourquin: http://manandmollusc.net/ )
- Micro Shells (defunct link: http://www.bigai.ne.jp/
)
- Molluscs.net: (defunct link:
http://www.molluscs.net/gallery/haliotidae/
)
- Seashells of New South Wales ( D.
L. Beechey: http://seashellsofnsw.org.au).
On a more general note, only
a limited number of shell assignments from the initial survey are
included here, partly because of the interim nature of the survey and
partly because of "concatentation" concerns (perhaps already
breached). Additional assignments will likely be included in
later papers following further refinements to the test procedures. For
the time being, the last example
from the survey is Thatcheria mirabilis (Angas 1877; k
= Phi 7/6, n =
1.753149344) 60 shown
below with an assignment based predominantly on the planview, but also
reinforced by a full-height assignment of the same spiral in the
vertical plane. This secondary, "three-dimensional" technique is
applicable to other shells,
but planviews are preferred for obvious reasons.
Fig.
18. Thatcheria mirabilis with the spiral k = Phi
7/6
TRANSITIONAL
REMARKS
As
for what may or may not lie at the root of such pronounced yet
regular variations that give rise to the apparent fit of pheidian
spirals to the shells discussed here, I do claim to have any concrete
answers to this complex matter, but I can at least show in Part B
what the Phedian Planorbidae may represent in fundamental
dynamic terms.
B. TO
GOVERN ALLTHINGS REVISITED
B.1.
THE PHEIDIAN
PLANORBIDAE AND ANGULAR MOMENTUM
1.1.
ANGULAR MOMENTUM AND INVERSE VELOCITY
The subject of angular momentum was addressed previously in both
Section III and and Section IV--in hypothetical terms
with respect to theoretical changes in the structure of the Solar
System in the former, and in more practical terms in the latter
concerning Period-Distance-Velocity relationships, i.e.,
T 2 = R 3
= Vr -6 (where
T represents the mean period of revolution, R the mean
heliocentric distance and Vr the mean orbital velocity) and: T
2 = R 3
= Vi 6 where
Vi is the mean inverse orbital velocity.
Here it may be observed that with respect to the Third (or Harmonic)
Law of planetary motion the determination of the mean heliocentric
distance
(R) from the mean sidereal period (T) is often given by
the exponential relationship: T 2 = R
3.
However, both the heliocentric distance (R) and mean orbital
velocity (Vr) may be obtained from the mean period (T)
(and vice versa ) from a number of additional relationships;40
the first (a variant of the general relationship already given) being
perhaps the best known:
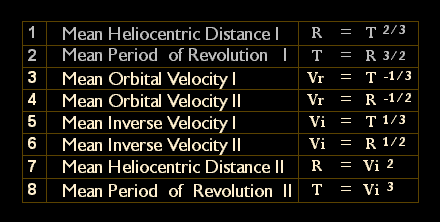
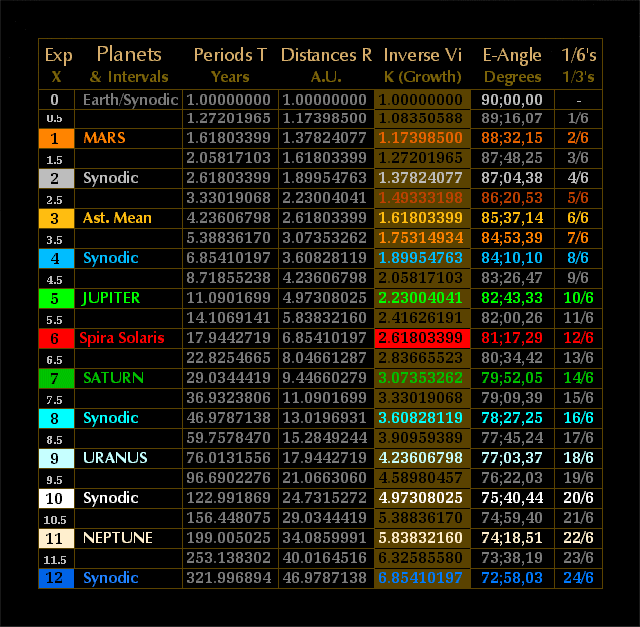
Table
1.
Pheidian Period, Distance and Velocity Relations
Mean velocities may, of
course, also be obtained from the fundamental relationship directly by
using negative fractional exponents (relations 2 and 3) or more simply
from the reciprocals of the inverse velocities
(relations 4 and 5), which are, of course, simply cube roots and square
roots. But the inclusion of the inverse velocity provides additional
benefits, not least of which being that the
Period-Distance-Inverse Velocity relationship T
2 = R 3
= Vi 6 allows the
inverse
velocity Vi to play a major role in the computation of
Angular Momentum (L). A brief and
informative introduction to this subject is given below (source:
Jeffrey K. Wagner, Introduction to the Solar System):41
Most of the
angular momentum of the solar system is in the planets, not in the Sun.
This is because the massive Sun rotates very slowly, whereas the
planets, less massive but far away, move rapidly enough in their
orbits that their angular momentum is greater. This is particularly
true for the gas giants. (Angular momentum is a quantity for rotating
or revolving objects that is somewhat analogous to momentum for objects
moving in a straight line. The angular momentum, L, of an orbiting
object is given by the equation L = mav, where m is the
mass of the object, a is its semi-major axis, and v
is its average orbital velocity. For a rotating object, angular
momentum is given by L
= Cmr2w, where
C is the object's moment of inertia coefficient, m
is its mass, r is its radius, and w is its
rotational velocity in radians per second. Table 29.1 lists the angular
momentum of various solar system objects.) Other important
characteristics of the solar system involve the physical properties of
its various objects. The planets differ in composition, with the
controlling factor being distance from the Sun. The inner, terrestrial planets are rocky and metallic,
the outer gas giants are primarily hydrogen and helium, and outermost
Pluto is icy. The planets and their satellites resemble miniature solar
systems, and most satellites orbit regularly in the equatorial plane of
their planet ... (Jeffrey K. wagner; Chap. 29. Constraints on
Solar System Formation in Introduction to the Solar System,
Holt, Rinehart & Winston, Orlando 1991:426)
Consequently
angular momentum is essentially the product of the mass (m),
the mean distance (R) and the mean
velocity (Vr).
However, because of the Period-Distance-Velocity relationship
T 2 = R 3
= Vi -6 and the
inverse
velocity variant, the formula: L = Mav may be expressed
in the form Mass x Vi 2x
Vr, which
reduces further to Mass x Vi. Thus, in simpler and
more practical terms:
Angular Momentum L = mvi
Angular momentum is often expressed in absolute terms,
but for
comparison and general purposes it may also be calculated with respect
to unity with Earth providing the frame of reference
for the mean periods, the mean distances, the mean velocities and
the planetary masses (e.g., the mass of Jupiter from this
viewpoint is 317.88 times that of Earth, etc.). Furthermore, while
still remaining with mean values it is also possible to compute the
angular momentum for the Phi-Series exponential planetary framework
directly. Thus we obtain the following comparison with Jeffrey K.
Wagner's estimates and the above relation:
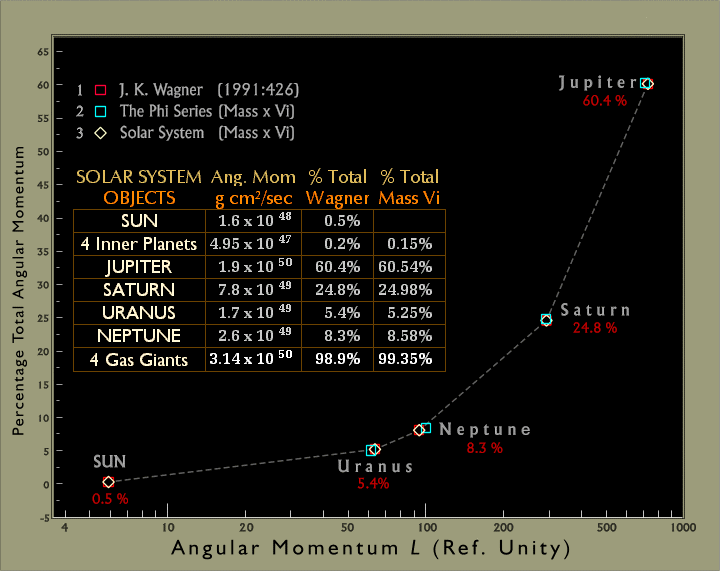
Table 2. Percent
Solar
System L, The Phi-Series Exponential Framework
and the Modern Solar System (after Wagner 1991:426)
As shown in Table 2,
the estimated percentage of the
total angular momentum of the Solar System possessed by each planet
departs little from the modern estimates provided by Jeffrey K. Wagner
(1991:426). Although
minimal, the main differences are precisely those expected for the
Phi-Series
planetary framework,
i.e., there is slightly less angular momentum
for
Uranus (the latter being theoretically closer to the Sun) and
correspondingly more for Neptune, which is theoretically more
distant.
It remains now to present the actual angular momentum for
the major planets computed for the Phi-series planetary framework with
the relation L = Vi x Mass. Thus, starting from Mars
(rather than Earth).
Working outwards it turns out that the resulting inverse velocities in
Table 3 below are simply the Pheidian Planorbidae --and
not only increasing by "Thirds" either, -- but also in due sequence,
extending from the inverse velocity of Mars ( k = Phi
1/3) out to Neptune (k =
Phi
11/3) with all intermediate synodic
positions
included. Thus the Growth factor k is in fact the
inverse velocity Vi --nothing more and nothing less,
with the angular momentum in each case simply the product of the pheidian
planorbidae and the planetary masses applied to modern data:
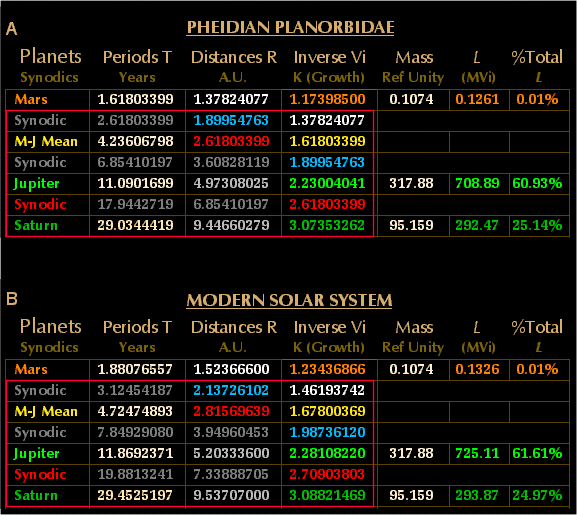
Table 3. Angular Momentum L,
and the Phi-Series Exponential Framework
Lastly, for this phase of
the investigation one further step is required, namely the insertion of
the Pheidian "Sixths" which, (as explained in Section IV) is by no
means as difficult as it might appear, as long as the associated
procedures and techniques are understood. Historically, the following
table is also of interest in so much as planet Earth, while
representing the starting point with a "growth" factor of 1 : 1 and
corresponding equiangle of ninety degrees, is in effect the "center"
--a primary position that is nevertheless more theoretical than
heliocentric per se.
The initial set of Pheidian Planorbidae
as tested are given below in exponential sixths out to the
twenty-fourth
(corresponding growth factor/expansion rate: k
= Phi 4):
Table 4. The Pheidian
Planorbidae:
Sixths; Growth Factors/Expansion Rates 1.084 to 6.854
In
diagrammatic form with the thirds alone, the following graphical
representation emphasizes the astronomical significance of the Pheidian
planorbidae and their relationship to the four major planets. Here
it now becomes apparent that Spira Solaris occupies a key position
between the two most massive planets in the Solar System, Jupiter and
Saturn--a situation further complicated by the elliptical nature of the
respective orbits of the latter pair, their known resonances and
further complexities concerning their inverse velocities with respect
to the mean velocity of Mars as discussed in Sections II and III (see
also below):
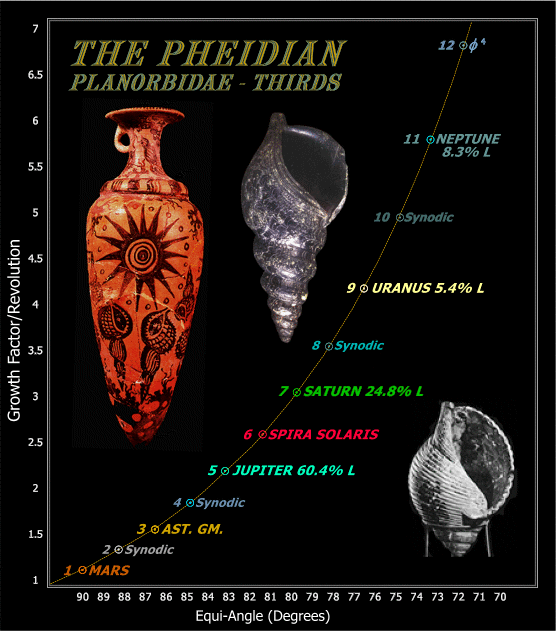 Fig. 19. The Phedian
Planorbidae in Astronomical Context
Fig. 19. The Phedian
Planorbidae in Astronomical Context
In Figure 19 the numbers to the
left of the planetary and intermediate
synodic positions represent the corresponding exponents that generate
the mean periods of the Phi-series exponential planetary framework.
Thus the mean sidereal period of Jupiter is Phi raised to
the
fifth power ( Phi 5=
11.090169944
years), Saturn: Phi raised to the seventh power ( Phi
7= 29.034441854 years) and Uranus Phi
raised to the
ninth ( Phi 9 =
76.013155618
years). For the inverse velocities, a.k.a the Pheidian growth
factors/expansion rates, these may be obtained by applying the cube
root to
the periods, or in a single step from the division of each period
exponent by three. Thus for Jupiter k = Vi = Phi
5/3; for Saturn k = Vi =
Phi 7/3; for Uranus k = Vi
= Phi 9/3,
and for good measure (between the first pair) Spira Solaris: k
= Vi = Phi 6/3 =
Phi 2.
In passing, it is not out of place to note here that the
occurrence of the Pheidian spiral k = Phi 2/3
among Conidae may be back-tracked with respect to the double
spiral and larger growth factors, i.e., k = Phi 2/3
raised to the fourth power is in turn k = Phi 8/3
now associated with the Saturn-Uranus synodic cycle, i.e.,
the eighth "third", with the other major synodic cycle (Spira Solaris)
the sixth. Thus there is a continuous integer range from 5
though 9 with the odd-number planetary assignments
predominating. For more on this aspect and its possible historical
ramifications,
see Historical
Complexities.
B2. INVERSE VELOCITY RELATIONSHIPS AND THE SOLAR SYSTEM
As for the dynamics of the matter, this too is
clearly a subject of great complexity--even restricted to mean
values and the Phi-based exponential planetary framework. Although
theoretical, the latter is at least complete, whereas the Solar
System itself, with the apparent gap between Mars and Jupiter, regular
variations arising from elliptical orbits, and inter-planetary
resonances is vastly more complex. Nevertheless, the awareness of the
relationship between inverse velocity Vi, planetary mass and
angular momentum permits the re-examination of the Inverse Velocity
relationships discussed in Section II and III with respect to the
superior planets (Uranus, Saturn and Jupiter) and the terrestrial
planets from a more dynamic perspective. The three inverse-velocity
relationships described in these earlier
sections were as follows:
- Vi Venus
- Vi Mercury approximates the mean velocity of Uranus
- Vi Saturn
- ViJupiter approximates the mean velocity of
Mars. [Relation 4b]
- Vi Saturn/Uranus
Synodic - ViJupiter/Saturn Synodic approximates
the mean velocity of the Venus-Earth synodic
cycle.[Relation 4s1]
Graphically (Figure 20
below), with the corresponding Phi-series inverse velocities for
Jupiter, Saturn and the Jupiter-Saturn synodic (Spira Solaris) included
for comparison, it will be noted that there are only minor differences
between phi-series values and those of the modern Solar System, i.e.,
for Jupiter: 2.281082 compared to 2.2300404 ( Phi 5/3);
Saturn: 3.088215 compared to 3.0735326 ( Phi 7/3)
and in between, the difference cycle Spira Solaris: 2.709038 compared
to 2.6180339 ( Phi 6/3) with
the latter
parameters also k, the Pheidian growth factor. The
linkage between the superior and inferior planets is shown
below:
 Fig. 20. The
Inverse
Velocity Relationships and the Solar System (Mean Values)
Fig. 20. The
Inverse
Velocity Relationships and the Solar System (Mean Values)
Although the data for
Figure 20 concerns mean values, for Spira Solaris in particular it is
also possible to consider the true variations that results from the
elliptical orbits of Jupiter and Saturn, as already treated in Section
II with respect to the mean and varying orbital velocity of Mars. Here
it was explained that subsequent testing provided the following results:
The inclusion of Earth
in this context--synodic location notwithstanding--thus serves to
augment the linkage between the Terrestrial planets of the lower
log-linear zone and the three gas giants of the outer zone. One or two
other inverse-velocity relationship also appear to exist that are
almost sequential--a qualifier necessary here in so much as the latter
appear to incorporate synodics and planetary inverse
velocities. But there are also other considerations and complications
to be addressed, for although mean values are applied in these
relationships, in real time such functions vary according to the
elliptical natures of the associated orbits. Nevertheless, in the case
of the Mars-Jupiter-Saturn relationship, with frames of reference
provided by the mean orbital velocity of Earth of 29.7859 kilometers
per second and 24.1309 kilometers per second for that of Mars,
real-time maxima and minima for Relation [4b] range between
19.66 and 28.3 kilometers per second, well
exceeding the extremal velocities of Mars itself.
However, utilizing the methods of Bretagon and Simon 44 adapted to generate sequential
data for 5-day intervals from 1700 to 2000 A. D., the mean
value nevertheless still turns out to be 24.0938 kilometers per
second. Similarly, the data for the real-time function based on
Relation [4s1] reveals that although there is
an even wider swing in extremal values, the mean value is also
comparable to that obtained from Relation [4s1] directly. All of
which is further complicated by the proximity of the Mars-Jupiter
synodic to the Earth-Mars synodic and various resonances known to exist
in the Solar System. (Spira Solaris, Part II. The Alternatives)
The third inverse
velocity relationship
brings with it further complications in so much as it represents the
combination
of the varying motion of three major superior
planets--Jupiter, Saturn
and Uranus--thus the effect of two adjacent difference cycles. Thus it
also
involves the three major adjacent planets that together possess over 90
percent of the entire Solar System's angular momentum, with the
Jupiter-Saturn difference cycle (i.e., Spira Solaris) at the 42 percent
position on the following chart:
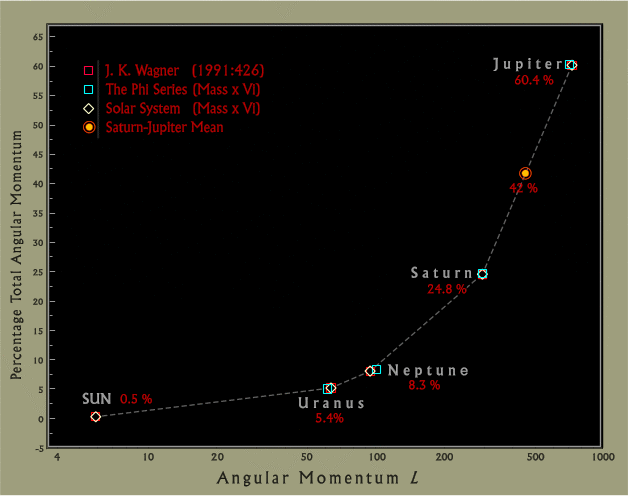
Fig.
21. The Distribution of Angular Momentum among the Major Planets
Given their massive sizes,
their prominence in terms of angular momentum and the cyclic, resonant
effects of their regular motions--all, if not synchronized with the
phi-series exponential framework, then periodically sweeping across it,
it is perhaps not that surprisingly if smaller objects such as Earth
and the other inferior planets should be influenced in one way or
another by the combined effects of the angular motion of larger bodies
such as Jupiter, Saturn, Uranus and Neptune. To which may
also be added further resonances among the inferior planets themselves,
augmenting perhaps the natural, local, diurnal, monthly and annual
cycles in turn.
How such events might or might not filter down to Earth
itself is a question that perhaps rightly
belongs to the first of things. And as such, it is perhaps largely
unknowable, but if in our times it is possible to a pursue a "Theory
of Everything" with a straight face and an apparently unerring aim,
then we might at least take up a few threads already woven into this
highly complex tapestry, starting with the lead provided by Louis
Agassiz.
B3.
SPECULATION CONCERNING ORIGINS
Just prior to launching into a detailed exposition of the application
of phyllotaxis to the Solar System first proposed by Benjamin Peirce in
184945 Louis Agassiz wrote in his famous Essay
on
Classification (1857):46
It must
occur to every reflecting mind, that the mutual relation and respective
parallelism of so many structural, embryonic, geological, and
geographical characteristics of the animal kingdom are the most
conclusive
proof that they were ordained by a reflective mind, while they
present at the same time the side of nature most accessible to our
intelligence, when seeking to penetrate the relations between finite
beings and the cause of their existence.
The phenomena of the inorganic world are all simple,
when compared to those of the organic world. There is not one of the
great physical agents, electricity, magnetism, heat, light, or chemical
affinity, which exhibits in its sphere as complicated phenomena as the
simplest organized beings; and we need not look for the highest among
the latter to find them presenting the same physical phenomena as are
manifested in the material world, besides those which are exclusively
peculiar to them. When then organized beings include everything
the material world contains and a
great deal more that is peculiarly their own, how could they be
produced by physical causes, and how can the physicists, acquainted
with the laws of the material world and who acknowledge that these laws
must have been established at the beginning, overlook that à
fortiori the more complicated laws which regulate the organic world, of
the existence
of which there is no trace for a long period upon the surface of the
earth, must have been established later and successively at the time
of the creation of the successive types of animals and plants?
(Louis Agassiz,Essay on
Classification, Ed. E. Lurie, Belknap Press, Cambridge
1962:127-128; emphases supplied)
Thus two points to
consider, firstly the physical environment, and secondly the inception
and the later flourishing of life as we understand it on Earth. As
for possible physical causes that may pertain to both, there cannot
be one without the other, and perhaps their origins are also
intertwined. To this end and with this in mind, consider the following
short discourse occasioned by Galileo's treatment of planetary motion
described somewhat circuitously in The Two New Sciences
(1609). Published in the Journal of the Royal Astronomical
Society of Canada in 1989 the parent paper was not merely a
historical commentary, it was also the source of the velocity
expansions of the laws of planetary motion applied throughout the
present series of essays, angular momentum included. Given below is the
short discussion that occurs at the end of the paper concerning a
possible percussive origin for the planets
attributed to Galileo, or at least the general line of inquiry that
he appears to have been pursuing:47
Could
Galileo have extended his treatment of terrestrial projectile paths to
embrace satellite orbits and also have expanded the idea one step
further to include the planets as satellites of the Sun? While
acknowledging that there are dangers in attributing to Galileo modern
or Newtonian concepts, it is necessary to recall that the initial
discussion of the parabola concerned the path traced by a projectile
with uniform horizontal velocity applied down the horizontal axis, and
"naturally accelerated" velocity applied down the vertical axis.
Visually, a projectile launched almost horizontally will obviously gain
very little height before falling back to ground when the initial
velocity is relatively low. As the initial velocity increases, however,
some height will be gained because of the curvature of the Earth, and
although the projectile may still fall to ground, with sufficient
velocity, a projectile will finally "fall" into orbit around Earth
itself. Thus in general, by reversing matters, all objects in
specific orbits may be treated in terms of a "percussive origins
theory" with the parent body the initial source. The hypothesis
may
therefore be applied to the planets and the Solar System with the Sun
as the single percussive point of origin.
Could
Galileo have taken this final step? If he did, then undoubtedly
criteria provided by Galileo in his historical aside becomes more
significant than ever, i.e., if planetary origins are considered in
terms of
projectiles originating from the Sun, the planets would indeed "start
with zero velocity" and "move through successive speeds" until their
initial "rectilinear motion" changed into "circular motion" (or orbital
motion) as they "fell" into their respective orbitals positions. And
once established, the planets would then "revolve without either
receding
from or approaching" their common point of origin, or deviating from
their "final" positions in the Solar System.
Although no causal mechanism is associated with this "percussive
origins" (or "Small Bang") theory, the hypothesis might possibly assume
that the
Sun was essentially formed at this stage, and for whatever reason,
the planetary material was ejected from the Sun in one enormous
explosion.
In
this sense the hypothesis is a variation of catastrophe theory, with
the exception that the source of the catastrophe is internal rather
than external. The latter, involving collisions or near misses with
double or triple stars, etc., are not generally well supported today,
but the percussive elements of the basic hypothesis may perhaps have
some affinity with
the massive explosion of the solar core (i.e., the "T Tauri winds")
thought by some accretion theorists to be a possible explanation for
the expulsion of unaccreted dust and gas from the Solar System. (John
N. Harris, "Projectiles,
Parabolas, and Velocity Expansions of the Laws of Planetary Motion,
" JRASC, Vol 83, No. 3, June 1989:207-218)
And the point here?
The matter of origins and the possible inception of ordering and
marshalling forces from the dynamic, resonant motions of the major
superior planets, not perhaps so much initially as later, though a
violent birth may also present an option.
Lastly, a real-time
illustration
of the significance of the motions of the two most masssive,
fibonacci-resonant
planets in the Solar System, their relationship to Spira Solaris, and
also
perhaps, to natural growth.
B.4.
THE
PHEIDIAN CONSTANT 2.61803398874 AND ITS INVERSE
0.381966011
REVISITED
From Part III (The Exponential Order)
the planetary period constant for the
Phi-series exponential
framework was determined to be Phi 2
= 2.61803398874, whereas the inverse (Phi -2
=
0.381966011)
is known to be closely related to the
"ideal" convergence angle in phyllotaxic contexts. However, the reader
will
recall that "Spira Solaris" (the all-inclusive equiangular "period"
spiral) was also based on the fundamental
constant
Phi
2 = 2.618033989.
This was the final result
of an investigation
that
had included mean planetary periods, synodic motion and orbital
velocities
in a search for logarithmic order in the structure of the Solar System
- a search
that was ultimately
reduced to the solution
of the quadratic formula that defines the Golden Section ( X 2
2-
X - 1 = 0 ).
The
initial result was therefore Phi itself = 1.618033989
for an exponential
planetary
framework incorporating the intervening synodic (lap) cycles between
adjacent
planets. For planet-to-planet increments the final period
constant
was therefore Phi
2
= 2.618033989.
As it so happens, the reciprocal
of
this
last value, Phi -2 = 0.381966011 is not only intimately related to
"ideal
angles" and natural growth, it is also a repeat parameter in the
Phi-Series
planetary framework, i.e., it occurs twice for Mercury (once for the
heliocentric
distance, and again for the Mercury-Venus synodic period. Thirdly, it
is also the
"velocity" (Vr) of the synodic difference cycle between Jupiter and
Saturn:

Fig.
21b.
Relations 14a-14e and the Ideal Growth Angle
These multiple occurrences
arise from the three-fold
nature of the Phi-Series Planetary Framework, which necessarily
incorporates identical values for periods, distances and velocities
according to their
exponential position in the planetary
framework, including
the Inverse
Velocities, which (as we have already seen above) play an
important role in the computation of angular momentum.
With this basis revisited, the well-known 60-year, 2 : 3 : 5 fibonacci resonance between
the two most massive planets in the Solar system (Jupiter and Saturn)
takes
on further significance as Table 5 and Figure 21c show,
for
the arithmetic mean of the actual Jupiter and Saturn mean
velocities
(Vr) is not only 0.381280708; the
daily
average function for this pair of planets computed for the 400-year
interval from 1600 -
2000
CE [Julian Day 2305447.5 through Julian Day 2451544.5 ] is in turn
found to be 0.381071579.
|
Planets
and
|
Periods
|
Distances
|
Velocity
Vr
|
Velocity
Vi
|
|
Synodics
|
(Years)
|
(A.U.)
|
(Ref.
Unity)
|
k (Growth)
|
| JUPITER |
11.868991 |
5.203264 |
0.438391444 |
2.28106642
|
| Synodic |
19.925328 |
7.349712
|
0.368862787 |
2.71103519 |
| SATURN |
29.354971 |
9.516000 |
0.324169972 |
3.08480145
|
Table 5b. The
Solar
System
Mean Values, Jupiter, Saturn and the J-S Synodic Cycle.
Arithmetic Mean: (
SaturnVr + JupiterVr) =
0.381280708
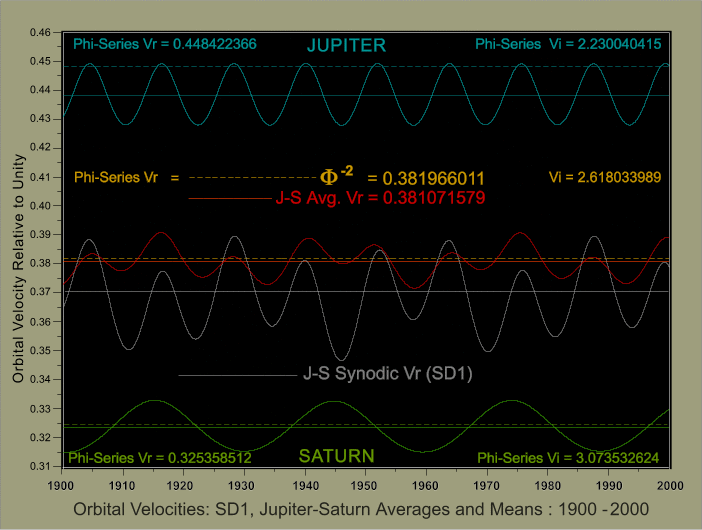
Fig.
21c.
The Jupiter-Saturn Average Velocity Function (JS-Avg.Vr) and the
Phyllotaxic
Constant k = Phi
-2
The above is
necessarily a
two-dimensional representation of the orbital motions of the two major
Fibonacci planets. Further
complications naturally arise from minor differences in the inclination
of the planetary planes, periodic changes in the lines of apsides, and
the fact
that the entire Solar System is (in a temporal sense) spiralling
towards the constellation of Hercules -- at
which point readers may like to examine -- either from the present
perspective, or indeed in its own right -- the insights and
complexities
in Gabi Mueller's Qualitative
Torkado Model
(includes English translation links); see also the latter's Golden Mean
iterations: http://www.torkado.de/phi.htm.
As for
the development of life on
Earth, or indeed anywhere, this no doubt
remains one of the great mysteries, but it may be that the three-fold
number and pythagorean tenets lie at the root of it to some extent at
least, and that there is both verity and wisdom in what has been handed
down to us concerning this matter, and the forces that: "Govern all things, and Order all
things not Ordered."
* * * * *
APPENDIX
THE MATTER OF LOST
LIGHT
As Sir Theodore Andrea Cook pointed out long ago (1914:414), there are
any number of equiangular spirals that lie between the limits set by a
straight line and a circle. Which may or may not provide a partial
explanation for the present lack of
progress in coming to terms with the many spiral configurations so
clearly evident in shells. This state of affairs is
especially surprising when the universal availability of the modern
computer is taken into consideration, but perhaps this is also part of
the problem, i.e., a general lack of focus allied to the use of the
computer as a toy rather than scientific tool. In fact forty years have
passed since David Raup48 first introduced
computer
simulation of shells, but little in the way of qualification or
quantification appears
to have followed thereafter. Instead, the subject appears to have been
spread so wide of late that it is in grave danger of dissipating
entirely
rather than being consolidated and refined further. Which again is
puzzling
given the start obtained in 1962, as Tony Phillips recounts 49
in "The
Mathematical Study of Mollusk Shells"
The paleontologist
David
Raup, then at Cornell, published a paper in 1962 (Science
138:150-152)
entitled "Computer as aid in describing form in gastropod shells." He
showed
how a computer could be programmed to make images of the equiangular
spiral
model with several parameters. To put this achievement in perspective:
the
term "computer graphics" was coined around 1960, and Spacewar,
the
first video game ever, was designed in 1961. What is even more
remarkable
is that a video sampling of Raup's models (which were made by tailoring
waveforms on an oscilloscope screen) is still on display in the Mollusk
galleries of the American Museum of Natural History in New York. My
chancing on that exhibit was the impetus for this column.
The video is part of an installation called "Spirals and
Shell Variation" which also includes wire
models and a variety of specimens. In the video, entitled "The Geometry
of the Coiled Shell," Raup gives a bare-bones presentation of the
potential of his method. Only three parameters are illustrated: rate of
aperture expansion, rate of departure from axis, and rate of descent
along axis; the parameter values are described ("0," "small," "large")
qualitatively. Seven different natural morphologies are simulated
(Nautilus, Spirula, Valvata, Goniobasis, Vermicularia, Anadonta
(a bivalve) and Bulla) with in most cases a specimen for
comparison.
Nor can it be said that
considerable
strides had not already been made years ago by the likes of Canon
Mosely (1838) and his contemporaries, or that the continuance of the
latter's treatment by Sir D'Arcy Wentworth Thompson was not widely
available (at least in the complete and unabridged edition of On
Grow and Form published in 1917, 1942 and 1992)50.
Take, for example, the
Nautilus,
the first shell mentioned in the above quotation, most likely the same Nautilus
that Sir D'Arcy Wentworth
Thompson declined to discus in detail because he preferred instead
(along with Mosely) to deal with the more complex turbinated shell
Turritella duplicata51.
For my own part I must admit that prior to April of this
year (2002) that I had not addressed the spiral formation in shells at
all, and moreover, I came across Sir D'Arcy Wentworth's seminal On
Growth and Form and the contributions of Canon Mosely rather late
in my inquiry. Partly, no doubt because of my less than perfect
methodology, but also partly because although the latter pair provide
by far the best starting point for spiral forms in shells, no clear
signposts to this effect were available to
point the way. Not only this, but two quite different versions of the
latter work exist, one with a sizeable amount of material pertaining to
shells and the entire chapter on phyllotaxis expunged in an abridged
edition first published a year before the Raup paper in 1961 and
reprinted thereafter in 1969, 1971, 1975, 1977, 1981, 1983, 1984, 1988,
1990, 1992, 1994, 1995, 1997and 2000. Here even the cross-section of the
Nautilus shown on the front page is degraded, though ultimately it
is still identifiable as k = Phi 7/3.
But in any case, my own analyses
proceeded from ammonites (by way of Simon Winchester's introduction
to the subject as noted above) to ramshorn snails, seashells and
the associated works of Sir Theodore Andrea Cook (The Curves
of Life, 1914), Samuel Colman (Nature's Harmonic Unity, 1911)
and then finally to the details in Thompson's On Growth and Form
(1917,1942). Because of this circuitous route I found that by initially
concentrating on two-dimensional growth factors that I had perhaps
naturally emulated Mosely's "characteristic" numbers. In the interim
I had also been working my way through various shells (some easy,
some difficult and some still unassigned) before finally coming across
the latter's analyses laid out in great detail by Sir D'Arcy Wentworth
Thompson. Having followed my own route, however, the "characteristic"
numbers discussed by the latter were by this time hardly new, in fact
for the most part they were immediately recognizable as two or
four-decimal place pheidian growth factors--specifically Phi
1/3, Phi 7/6and
Phi
1/4--the latter pair being rarer in
my own limited
experience, with k = Phi 7/6
(growth
factor: 1.753149344) given by Mosely to two decimal places as 1.75.
All this, mind you, by 1838, while the Raup approach still
apparently provides little or no integration or semblance of order.
Indeed, during the ammonite phase of testing it so happened that one of
the ammonites examined was Euhopites truncatus Spath 1925 from
the collection of the late Jim Craig,52 which
coincidentally
was also discussed in the above paper. The results of the respective
assignments for this example are shown below with Spira Solaris
positioned firstly with respect to the inner visible spiral, secondly
with respect to the outline [ I ], and next [ II ]
superimposed on the somewhat angular spiral
generated by the Raup approach, the latter thus also essentially Spira
Solaris.
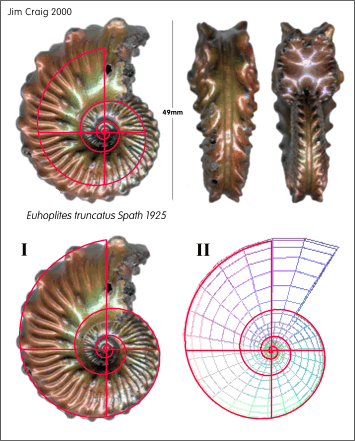 Fig. 22. Ammonite
Euhoplites truncatus Spath 1925 and the single spiral k = Phi 2
Fig. 22. Ammonite
Euhoplites truncatus Spath 1925 and the single spiral k = Phi 2
The difference, being of course,
that there are no trial and error
operations attending Spiral Solaris, or indeed any of the Pheidian
planorbidae. Moreover, there is a
great deal that can be accomplished before the introduction of
the third dimension, which has perhaps been part of the problem in
recent times, namely a general lack of focus coupled with a dearth
of choices. Too inviting a diversion, and also too distracting, it
would seem. Other matches from the above paper include a side view fit
for Nautilus pompilus (as before, k = Phi 7/3);
the ammonite Astroceras obtusum ( k = Phi 5/3),
Bellerophina minuta ( k = Phi 2/3):
Fig. 22a. The single spirals k = Phi 7/3, k = Phi 5/3
and k = Phi 2/3
plus bi-valve Mya arenia (a rare side view: k =
Phi 10). It should be noted here
that mathematical
details are certainly presented in abundance the above paper, but
perhaps in too much multi-dimensional detail to provide order and
connectivity, at least in pheidian terms.
This appears to be
a prevailing problem at present, for computer generated profusion and
dispersion also occurs in science popularist Richard Dawkins'
"Museum of All Shells" (Climbing Mount Improbable, 1996).53
Then again,
it is difficult to know what to make of a book that although dealing
with natural growth does not even mention the Fibonacci Series in the
Index. Nor do some of the more sophisticated methods involving
the use of computers in this book appear to have been well maximized
either,
e.g., Fig. 2.10.d ("Computer
tracing of a particular
spider's positions as it spins a web. MoveWatch program written by
Sam Zschokke.") records an auxiliary spiral constructed by the spider
Aruneus diademus,54 which though
somewhat irregular
nevertheless provides a ready fit for the pheidian spiral k =
Phi 2/3.
Fig. 22b. Web of Aruneus diademus and the single
spiral k = Phi 2/3
But there is more to the engineering
prowess of the spider in any case, not least of all its outer
commencement point and inward motion during web construction--logical
enough and necessary perhaps, but the implications remain profound.
And so, sadly, are the implications of the apparent
decline in understanding that appears to have followed successful
investigations into the spiral formation in nature
carried out over the last three centuries. Particularly in the
case of shells, it would seem, but it was not the general treatment
of this subject in Sir D'Arcy Wentworth Thompson's voluminous On
Growth and Form that served to emphasize the decline, but Canon
Mosely's convoluted treatment of the shell Turbo duplicata
in 1838. Indeed, one glance at the data and the means of presentation
was enough to elicit both surprise and great admiration--as D'Arcy
Wentworth Thompson duly noted in On Growth and Form--"Canon
Mosely
was a man of great and versatile ability" 55and
here was
at least partly why.
But for myself it was something else in addition. In
pursuing the line of inquiry followed by Galileo in a 1989 paper
entitled: " Projectiles,
Parabolas, and Velocity Expansions of the Laws of Planetary Motion" (Journal
of the Royal Astronomical Society of Canada; RASC, Vol 83,
No. 3,1989:207-218) I had long been puzzled by the obvious fact that if
I could deduce what Galileo had laid out in the New Sciences
(he had, after all, left sufficient clues) then others should surely
have been able
to do the same. Now it would appear that some indeed had, and well
before
my time in addition, including both Canon Moseley (1838) and Sir D'Arcy
Wentworth Thompson (1917). Nor does there seem to be much doubt about
this either; it is quite clear what Mosely delivered with his analysis
of Turbo duplicata, and equally clear that Thompson understood
it when he in
turn passed along the essence of the matter.
As for the relevant details, first of all, how well did Canon
Mosely fare with Turbo duplicata ?
Well enough, even in general terms, successfully arriving at the
characteristic number (k) of 1.1806 compared to
that of the pheidian spiral k = Phi 1/3
(1.1739)--as the latter scale applied to Mosely's illustration
of the shell in question shows:
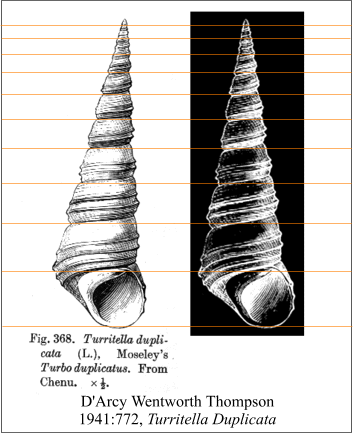
Fig.
23. Canon Mosely's Turritella Duplicata with the scale
of the spiral k = Phi 1/3
But
Mosely's treatment
was far from simple, and to explain it in detail it is necessary to ask
the
reader to recall some of the steps taken so far in the present inquiry.
Firstly,
with respect to the astronomical side of the Pheidian planorbidae,
it is necessary to remember that the growth factor k
(Mosely's
"Characteristic number") is the mean orbital inverse velocity (Vi);
secondly, remember also the relationships between the mean planetary
periods
(T), the mean heliocentric distances (R) and the mean
inverse
velocities (Vi), especially relations 4 and 5 from Table 1: Mean
Inverse
Velocity (Vi) = T 1/3 and also Mean Inverse Velocity (Vi)
= R 1/2.
Finally, note that the published "Velocity Expansions of the Laws of
Planetary Motion" attributed to Galileo in the above mentioned paper
were those given in the first line of the abstract, i.e.:
Kepler's
Third Law of planetary motion: T2 = R3 (
T = period in years, R = mean distance in astronomical
units ) may be extended to include the inverse of the mean speed Vi
( in units of the inverse of the Earth's mean orbital speed ) such
that: R = Vi 2 and T 2= R 3
= Vi 6
Additional relationships
were also introduced, but the above represents the deducable essence of
the matter--information that is quite sufficient for present purposes
in so much as it leads readily enough to relations 4 and 5. With
this in mind we may now turn to Canon Mosley's unusual treatment of the
spiral formations of Turbo duplicata recounted by Sir D'Arcy
Wentworth Thompson (1917:773) 56
From the apex of
a large Turritella (Turbo) duplicata a line was drawn
across its whorls, and their widths were measured upon it in
succession, beginning with the last but one. The measure ments were, as
before, made with a
fine pair of compasses and a diagonal scale. The sight was assisted by
a magnifying glass. In a parallel column to the following
admeasurements are the terms of a geometric progression, whose first
term is the width of the widest whorl measured, and whose common ratio
is 1.1804. [tables and data omitted ]
........
The close coincidence between the observed and
the calculated figures is very remarkable, and is amply sufficient to
justify the conclusion that we are here dealing with a true logarithmic
spiral. Nevertheless, in order to verify his conclusion still further,
and to get partially rid of the inaccuracies due to successive small
measurements, Moseley proceeded to investigate the, same shell,
measuring not single whorls but groups of whorls taken several at a
time: making use of the following property of a geometrical
progression, that "if
u represent the ratio of the sum of every even number (m ) of its
terms to the sum of half that number of terms, then the common ratio (r
) of the series is represented by the formula: r = (u - 1) 2/m .
So far, all of this is
fascinating in its detail, exactitude and the amount of measurement
involved, but it is next part that contains the hidden pearl. Given
below in graphical form to match that presented by Sir D'Arcy Wentworth
Thompson, the analysis proceeds as follows:
Notwithstanding the
methodology, nor being being overly critical, it still seems an
unnecessarily convoluted determination, and moreover, in spite of
Mosely's confident statement that "It is scarcely possible to imagine a
more accurate verification than is deduced from these larger
admeasurements," the last relation "r = (1.389)1/2
=
1.1806" is in fact incorrect--the actual result--1.1785--being on the other
side of Phi 1/3
(1.17398) . But what
certainly is correct is the following restatement of the last
two relations using accurate pheidian values, firstly to four decimal
places (after Mosely), and secondly to ten:

And yes, the
key values given by Mosely (1.645 and 1.389) are indeed "larger
admeasurements" compared to their pheidian counterparts--1.618 and
1.378 respectively. It is true that in the above r is applied
in all cases, but it is still astronomically correct in the lower
instance. Moreover, Mosely provided in thinly disguised form not only
the Golden Ratio, but also by demonstrating the application of the cube
and square roots the methodology leading to the mean sidered period
(1.618033989), the mean heliocentric distance (1.378240772) and the
corresponding mean inverse orbital velocity (1.173984997), i.e., the
essence and the root of the Phi-series planetary framework with the
last value also
the characteristic number, or growth factor k for the
shell in question. And having achieved this considerable goal, Mosley
did indeed "with safety" not only annex the species Turbo duplicatus,
he also passed on his insights in time-honoured tradition, ably
assisted by Sir D'Arcy Wentworth Thompson, who in turn passed it on
into the next century.
Unfortunately, this part is missing in the abridged edition of On
Growth and Form, as is the entire chapter on Phyllotaxis with its
copious notes and related references.
There is a great deal more, of course, that could be said
concerning the details and the methodology applied to the fitting of
spirals forms to shells and many other natural applications provided in
Thompson's voluminous On Growth and Form. And indeed in other
works
that for a brief time seem to have flourished around the beginning of
the last century. The above is included here because it epitomizes the
darker, stumbling side of human progress. And also the realization that
when Thomas Taylor (Introduction
to Life and Theology of Orpheus) speaks of social decline, loss
of knowledge in ancient times and the efforts to preserve it by those
who, "though they
lived in a base age" nevertheless "happily fathomed the depth of
their great master's works, luminously and copiously developed their
recondite meaning, and benevolently communicated it in their writings
for the general good," that sadly, such times are still upon us.
Thus, just as Sir Theodore Andrea Cook, who in the Curves of Life
(1914) was unable to define the "well known logarithmic spiral" equated
in 1881 with the chemical elements (see the previous section), neither
Mosely nor Thompson were able write openly about the either the Golden
Ratio or the Pheidian planorbidae. Nor unto the present day, it seems
have
others, for if not a forbidden subject per se, it long seems to
have been a poor career choice, so to speak. Moreover, even after Louis
Agassiz introduced Benjamin Pierce's phyllotaxic approach to structure
of the Solar System in his Essay on Classification (1857) the
matter was swiftly dispatched and rarely referred to again. A possibly
momentous shift in awareness, shunted aside with greatest of ease, as
the editor of Essay
on Classification, (E. Lurie) explained in the short loaded footnote57discussed
in the previous section. Nor it would seem, were the works of Arthur
Harry Church (On the Relation of Phyllotaxis to Mechanical Law,
1904)58 or Samuel Colman (Nature's
Harmonic Unity,
1911) 59allowed
to take root. Nor again were the lines of inquiry laid out in Jay
Hambidge's (Dynamic Symmetry 1920) permitted to have much
on effect on the status quo either, not to mention Sir
Theordore
Andrea Cook's Curves of Life (1914) and the general the thrust
of the many papers published during the previous century.
Where does this obfuscation and stagnation leaves us now?
Wondering perhaps where we might be today if the implications of the
phyllotaxic side of the matter introduced in 1849 by Benjamin Pierce
had at least been allowed to filter into the mainstream of knowledge
with its wider, all-inclusive perspective concerning "life" as we
currently understand it. The realization, perhaps, that we may indeed
belong to something larger than ourselves, and that as an integral,
living part of the Solar System rather than an isolated destructive
apex, that we should conduct ourselves with more care and consideration
towards all forms of life. Nor can we be in the least encouraged by the
fact that since that time there have been almost continual outbreaks of
local and international violence on Earth, including two major global
conflicts with the imminent threat of another looming on the darkening
horizon.*
And here we might also ask whether humankind was truly
well-served over the past century or so by the continued preservation
of the status quo and the agendas of special interest groups,
and because of this, whether we will even survive the madness of our
times, let alone come of age.
*
Written
in 2002. Matters
have hardly improved since
this time ...
END
OF PART
IVD2c
REFERENCES
- Winchester, Simon. The
Map that Changed the World, Harper Collins, New York 2001.
- Thomson, Sir D'Arcy
Wentworth. On
Growth and Form, Cambridge University Press, Cambridge 1942;
Dover Books, Minneola 1992.
- Huntley, H. E. The
Divine Proportion: A Study of Mathematical Beauty, Dover,
New York 1970.
- Kappraff, Jay. Connections:The
Geometric Bridge Between Art and Science, McGraw-Hill, New York
1991.
- Arganbright, Deane.
PHB Practical Handbook of Spreadsheet Curves and Geometric Construction,
CRC
Press, Boca Raton 1993.
- Cook, Sir Theodore
Andrea. The
Curves of Life, Dover, New York 1978; republication
of the London (1914) edition.
- Colman, Samuel. Nature's
Harmonic Unity, Benjamin Blom, New York 1971.
- Mosely, Rev. H. "On
the geometrical forms of turbinated and discoid shells," Phil. trans.
Pt. 1. 1838:351-370.
- Thomson, Sir D'Arcy
Wentworth. On Growth and Form, Cambridge University Press,
Cambridge 1942; Dover Books, Minneola 1992.
- Nauman, C.F. "Ueber
die Spiralen von Conchylieu," Abh. k. sachs. Ges. 1846; "Ueber
die cyclocentrische Conchospirale u. uber das Windungsgetz von
Planorbis corneus," ibid.
I, 1849:171-195; "Spirale von Nautilus u. Ammonites galeatus, Ber.
k. sachs. Ges. II, 1848:26; Spirale von Amm. Ramsaueri, ibid.
XVI, 1864:21.
- Muller, J. "Beitrag
zur Konchyliometrie," Poggend. Ann. LXXXVI, 1850:533; ibid.
XC 1853:323.
- Macalister, A.
"Observations on the mode of growth of discoid and turbinated shells," Proc.
R.S. XVIII, 1870:529-532.
- Telescopium
telescopium Linneaus
1758. Source: S. Peter Dance, Shells and Shell Collecting,
Hamlyn Publishing Group, London 1972:32.
- Conus princeps f.
lineolatus Valenciennes1832. Source: G. Paganelli, Conus
princeps f. lineolatus 1197. coneshell.net
- Architectonica
perspectiva Linneaus 1758. Source: S. Peter Dance, Shells and
Shell Collecting, Hamlyn Publishing Group, London 1972:52-53.
- Harpa kajiyamai Rehder
1973.Source: Machiko Yamada, (Defunct
link: http://www.bigai.ne.jp/pic_book/data20/r001967.html)
- Pedinogyra hayii
Griffith & Pidgeon 1833 (Hay's Flat-whorled Snail). Source: Machiko
Yamada (Defunct link:
http://www.bigai.ne.jp/pic_book/data20/r001967.html)
- Planorbis corneus,
Linnaeus 1758;
Source: Martin Kohl, (Defunct link:
http://members.aol.com/Mkohl1/Pulmonata.html)
- Nautilus pompilus,
Linnaeus
1758. Source: SEASHELLS. World of Nature Series, W.H.
Smith, New York.
- Haliotis brazieri,
Angas 1869. Source: D. L. Beechey, Haliotis
brazieri; Index: Shells of New South Wales. 20a. Haliotis brazieri (smooth
form variant)
- Haliotis
scalaris, Leach 1814, Source: Machiko Yamada,
(Defunct
link: http://www.bigai.ne.jp/pic_book/data20/r001967.html)
- Thompson, Sir D'Arcy
Wentworth. On Growth and Form, 1992:
- Conus mercator, Linnaeus 1758 and Conus ammiralis f. hereditarius DA MOTTA, 1987. Source: G. Paganelli, coneshell.net
- Conus tulipa, Linnaeus
1758. Source: G. Paganelli, Conus tulipa 710,
coneshell.net
- Thompson, Sir
D'Arcy Wentworth. On Growth and Form, 1992:816.
- Harpa goodwini.
Source: Guido T. Poppe, Conchology (Defunct link:
http://www.conchology.uunethost.be/ )
- Clarke, Arthur H.The
Freshwater Molluscs of Canada, National Museum of Natural Sciences,
Ottawa 1981.
- ibid., p.175.
- Kohl, Martin. Freshwater
Molluscan Shells: Planorbidae (Defunct link:
http://members.aol.com/mkohl2/Planorbidae.html)
- Ovid, as quoted by
Nicole Oresme in Du Ciel et du monde, Book II, Chapter
25, fols. 144a-144b, p.537.
- Liguus virgineus
Linnaeus, 1758. Source: Harry Lee, jaxshells.org: http://www.jaxshells.org/ligver.htm
Index: http://www.jaxshells.org/
- Helisoma pilsbryi
infracarinatum (Great Carinate Ramshorn Snail, Baker 1932).
Source:
Arthur H. Clarke.The
Freshwater Molluscs of Canada, National Museum of Natural
Sciences, Ottawa 1981:210.
- Helisoma
(pierosoma) corpulentum corpulentum (Capacious Manitoba Ramshorn
Snail , Say 1824). Source: Arthur H. Clarke. The
Freshwater
Molluscs of Canada, Ottawa 1981:206.
- Promenetus
exacuous megas (
Broad Promenetus Dall, 1905. Source: Arthur H. Clarke.The Freshwater
Molluscs of Canada, National Museum of Natural Sciences, Ottawa
1981:189.
- Thompson, Sir
D'Arcy Wentworth, On Growth and Form, 1992:751-753.
- Hambidge, Jay. Dynamic
Symmetry,
Yale University
Press, New Haven 1920:16-18.
- Kappraff, Jay. Connections:The
Geometric Bridge Between Art and Science, McGraw-Hill, New York
1991:46.
- Thompson, Sir
D'Arcy Wentworth, On Growth and Form, 1992:791.
- Haliotis parva,
Linnaeus 1758. Source: Molluscs.net: Haliotis
parva; Index: http://www.molluscs.net/
- Harris, John N.
"Projectiles, Parabolas, and Velocity Expansions of the Laws of
Planetary Motion," JRASC, Vol 83, No. 3, June 1989:207-218.
- Wagner, Jeffrey K. Introduction
to the Solar System, Holt, Rinehart & Winston, Orlando 1991:426.
- Marine decorated
rhyton from Zakros
(Crete). Wondrous Realms of the Aegean, selected by the
editors, Lost Civilizations Series, Time-Life Books, Virginia 1993:110.
- Embossed, carved
12-inch rhyton from Zakros (Crete). Wondrous Realms of the Aegean,
selected by the editors, Lost Civilizations Series, Time-Life Books,
Virginia 1993:99.
- Bretagnon, Pierre and
Jean-Louis Simon, Planetary Programs and Tables from -4000 to +2800,
Willman-Bell, Inc. Richmond, 1986.
- Pierce, Benjamin. "Mathematical Investigations of
the Fractions Which Occur in Phyllotaxis," Proceedings, AAAS, II
1850:444-447.
- Agassiz, Louis. Essay
On Classification, Ed. E. Lurie, Belknap Press, Cambridge
1962:127-128.
- Harris, John N.
"Projectiles, Parabolas,
and Velocity Expansions of the Laws of Planetary Motion, " JRASC,
Vol 83, No. 3, June 1989:216.
- Raup,
David. "Computer as aid in describing form in gastropod shells," Science
138, 1962:150-152.
- Phillips, Tony and
Stony Brook, "The
Mathematical Study of Mollusk Shells" American Mathematical
Society; AMS.ORG.
- Thompson, Sir D'Arcy
Wentworth. On Growth and Form, Cambridge University Press,
Cambridge 1942; the complete unabridged reprint, Dover Books, Minneola
1992.
- Turritella duplicata,
Source: Canon Mosely, in Sir D'Arcy Wentworth Thompson, On
Growth and Form, the complete unabridged edition, 1992:772.
- Euhoplites truncatus
(Spath 1925).
Source: Jim Craig: Euhoplites
truncatus. Index: Fossils
of the Gault Clay
and Folkestone Beds of Kent, UK
- Dawkins, Richard. Climbing
Mount Improbable, W.W. Norton, New York 1996:198:223.
- _____________
Aruneus diademus Spider.Climbing
Mount Improbable, Norton, New York 1996:58.
- On Growth and Form,
1942:784.
- On Growth and Form,
1942:773.
- Lurie, E. (Ed.) Essay
On Classification, Belknap Press, Cambridge 1962:128.
- Church, Arthur Harry. On
The Relation
of Phyllotaxis to Mechanical Law, Williams and Norgate, London
1904; see also: http://www.sacredscience.com
(cat #154).
- Colman, Samuel. Nature's
Harmonic Unity, Benjamin Blom, New York 1971:3.
- Thatcheria mirabilis
(Angas 1877). Source: Mathew Ward, Photographer; in Peter S. Dance,
Shells, Stoddart, Toronto 1992.
- Hildoceras
bifrons, (Bruguière 1789). Figure 1b2.
Source: Hervé Châtelier, Ammonites et autres
spirales
- Hervé Châtelier.
- Dactylioceras
commune (Sowerby 1815). Figure
1Ca.
Source: Hervé Châtelier, Ammonites et autres
spirales.
- Porpoceras vortex
(Simpson 1855). Figure
1Cb.
Source: Hervé Châtelier, Ammonites et autres
spirales.
- Protetragonites
oblique-strangulatus
(Kilian 1888). Figure
1Cc.
Source: Hervé Châtelier, Ammonites et autres
spirales.
- Lytoceras cornucopia
(Young & Bird 1822). Figure
1Cd. Source: Hervé Châtelier, Ammonites
et
autres spirales.
-
Epophioceras
sp. (Spath, 1923). Figure
1D. Source: Christopher M.
Pamplin, (Defunct link: Lower
Jurassic Ammonites. http://ammonites.port5.com/epop.htm)
-
-
- Ethioceras raricostatum (Figure
1e). Line drawing by Soun Vannithone, in Winchester, Simon. The
Map that Changed the World, Harper Collins, New York 2001:1
Copyright © 2002. John N. Harris,
M.A.(CMNS). Last
updated on March 31, 2009. Cosmetic update October 9, 2010.
Ammonite graphics (Figures 1b2, 1c and 1d)
added
on April 29, 2003; Figure 21c on June 4 2003; Figure. 7b added 11 May,
2004; Figures 22a, 22b, and 1d3 added 17 July, 2004. Figures1 and 1e on
18 July, 2004.
Return to Spira Solaris
PREVIOUS SECTION
NEXT SECTION