
PART IVd2b.
THE THREE-FOLD NUMBER

PART IVd2b.
THE THREE-FOLD NUMBER
A. TO GOVERN ALL THINGS
So much, then, for our program as a whole. But to crown it all, we must go on to the generation of things divine, the fairest and most heavenly spectacle God has vouchsafed to the eye of man. And: believe me, no man will ever behold that spectacle without the studies we have described, and so be able to boast that he has won it by an easy route. Moreover, in all our sessions for study we are to relate the single fact to its species; there are questions to be asked and erroneous theses to be refuted. We may truly say that this is ever the prime test, and the best a man can have; as for tests that profess to be such but are not, there is no labor so fruitlessly thrown away as that spent on them. We must also grasp the accuracy of the periodic times and the precision with which they complete the various celestial motions, and this is where a believer in our doctrine that soul is both older and more divine than body will appreciate the beauty and justice of the saying that ' all things are full of gods ' and that we have never been left unheeded by the forgetfulness or carelessness of the higher powers. There is one observation to be made about all such matters. If a man grasps the several questions aright, the benefit accruing to him who thus learns his lesson in the proper way is great indeed; if he cannot, 'twill ever be the better course to call on God. Now the proper way is this--so much explanation is unavoidable. To the man who pursues his studies in the proper way, all geometric constructions, all systems of numbers, all duly constituted melodic progressions, the single ordered scheme of all celestial revolutions, should disclose themselves, and disclose themselves they will, if, as I say, a man pursues his studies aright with his mind's eye fixed on their single end. As such a man reflects, he will receive the revelation of a single bond of natural interconnection between all these problems. If such matters are handled in any other spirit, a man, as I am saying, will need to invoke his luck. We may rest assured that without these qualifications the happy will not make their appearance in any society; this is the method, this the pabulum, these the studies demanded; hard or easy, this is the road we must tread. (Epinomis, 989d-992a, Trans. A.E. Taylor, The Collected Dialogues of Plato, Princeton University Press, Princeton, 1982:1530-31; emphases supplied)
... For these reasons and from such constituents, four in number, the body of the universe was brought into being, coming into concord by means of proportion, and from these it acquired Amity, so that coming into unity with itself it became indissoluble by any other save him who bound it together. (Timaeus, 31b-32c, Plato's Cosmology: The Timaeus of Plato, Trans. Francis MacDonald Cornford, Bobbs-Merrill, Indianapolis, 1975:44, emphases supplied) 2
it is conceivable that the parameters and structure of Spira Solaris might provide not only the necessary element of "luck", but also some degree of understanding concerning the "binding." Certainly there are enough parameters and associated concepts available (both past and present) as already touched upon in the last two sections. However, it would still be optimistic to expect that either the application or the precise details would be immediately apparent. In fact--after the manner of Orpheus, Pythagoras and Plato--it might well be that certain related matters were indeed: "promulgated mystically and symbolically (by the first); by the second, enigmatically and through images; and scientifically by the third." Or, as Thomas Taylor put it: "conformably to the custom of the most ancient philosophers, (information) was delivered synoptically, and in such a way as to be inaccessible to the vulgar."
Said Aristotle, prince of philosophers and never-failing friend of truth:
All things are three; The three-fold number is present in all things whatsoever...
Nor did we ourselves discover this number, but rather natures teaches it to us.
The Monad is enlarged, which generates Two.
For the Dyad sits by him, and glitters with Intellectual Sections.
And to govern all things, and to order all things not ordered.
For in the whole World shineth the Triad, over which the Monad Rules.
This Order is the beginning of all Section.
for the Mind of the Father said, that all things can be cut into three,
Governing all things by mind.
........
The Center from which all (lines) which way soever are equal.
for the paternal Mind sowed Symbols through the World.
...........
Fountain of Fountains, and of all Fountains.
The Matrix containing all things . . .
The content of the above passage from the Chaldean Oracles may surprise some readers, but nevertheless the historical side of the matter is not that difficult, although it is clearly out of kilter. The Fibonacci series (and thereafter the Golden Ratio) have long been associated with natural growth from Fibonacci onwards for the moderns, through Kepler, and later via the efforts of a veritable host of investigators, as R.C. Archibald's lengthy Bibliography 5 in Jay Hambidge's Dynamic Symmetry (1920:146-156) 6 clearly attests. Though "to err is human," noticeably absent from the latter list are the contributions of Samuel Coleman (Nature's Harmonic Unity,1911)7 and those of Louis Agassiz 8 Essay on Classification, 1857)--but more on these omissions later. In passing, though, it is relevant to point out that the claim that the Fibonacci series was only discovered in the early part of the second millennium is surely invalid--a doubly ignorant assertion (in Thomas Taylor's understanding of the term) that in any case was largely demolished by D'arcy Wentworth Thompson years ago as follows: 9
The Greeks were familiar with the series 2, 3 : 5, 7 : 12, 17, etc.; which converges to 21/2 as the other (i.e., the Fibonacci series) does to the Golden Mean; and so closely related are the two series, that it seems impossible that the Greeks could have known the one and remained ignorant of the other. (Sir D'arcy Wentworth Thompson, On Growth an Form, Dover, New York 1992:923; unabridged reprint of the 1942 edition)
The latter also pointed out, however, that:10
We must not suppose the Fibonacci numbers to have any exclusive relation to the Golden Mean; for arithmetic teaches us that, beginning with any two numbers whatsoever, we are led by successive summations toward one out of innumerable series of numbers whose ratios one to another converge to the Golden Mean ( (Sir D'arcy Wentworth Thompson, On Growth an Form, Dover, New York 1992:933; unabridged reprint of the 1942 edition)
This is true enough, but it also adds weight to his previous observation.
For example, consider the following Pythagorean reference (or mnemonic device, if one prefers) concerning the number 36 as explained by W. Wyn Westcott:11
Plutarch, "De Iside et Osiride," calls the Tetractys the power of the number 36, and on this was the greatest oath of the Pythagoreans sworn: and it was denominated the World, in consequence of its being composed of the first four even and the first four odd numbers; for 1 and 3 and 5 and 7 are 16; add 2 and 4 and 6 and 8, and obtain 36. (W.Wyn Westcott, Numbers: their Occult Power and Mystic Virtues, Sun Publishing Santa Fe, 1983:114).
A.2.
THE THREE-FOLD NUMBER AND THE "IDEAL"
DIVERGENCE ANGLE
Whereas the constant Phi 2provided the fundamental basis for the exponential
planetary framework, its importance with respect to natural growth and
phyllotaxis
has long been known, especially with respect to the phi-based "divergence angle",
along
with its possible relationship to "the domain of pure physics"
(Cook,
1914:414).12 A more up-to-date summary and
description of the
latter aspect was in fact recently provided by mathematician Ian
Stewart
in 1995 as follows:13
The most dramatic insight yet comes from some very recent work of the French mathematical physicists Stephane Douady and Yves Couder. They devised a theory of the dynamics of plant growth and used computer models and laboratory experiments to show that it accounts for the Fibonacci pattern.
The basic idea is an old one. If you look at the tip of the shoot of a growing plant, you can detect the bits and pieces from which all the main features of the plant?leaves, petals, sepals, riorots, or whatever?develop. At the center of the tip is a circular region of tissue with no special features, called the apex. Around the apex, one by one, tiny lumps form, called primordia. Each primordium migrates away from the apex?or, more accurately, the apex grows away from the lump?and eventually the lump develops into a leaf, petal, or the like. Moreover, the general arrangement of those features is laid down right at the start, as the primordia form. So basically all you have to do is explain why you see spiral shapes and Fibonacci numbers in the primordia.
The first step is to realize that the spirals most apparent to the eye are not fundamental. The most important spiral is formed by considering the primordia in their order of appearance. Primordia that appear earlier migrate farther, so you can deduce the order of appearance from the distance away from the apex. What you find is that successive primordia are spaced rather sparsely along a tightly wound spiral, called the generative spiral. The human eye picks out the Fibonacci spirals because they are formed from primordia that appear near each other in space; but it is the sequence in time that really matters.
The essential quantitative feature is the angle between successive primordia. Imagine drawing lines from the centers of successive primordia to the center of the apex and measuring the angle between them. Successive angles are pretty much equal; their common value is called the divergence angle. In other words, the primordia are equally spaced?in an angular sense?long the generative spiral. Moreover, the divergence angle is usually very close to 137.5°, a fact first emphasized in 1837 by the crystallographer Auguste Bravais and his brother Louis. To see why that number is significant, take two consecutive numbers in the Fibonacci series: for example, 34 and 55. Now form the corresponding fraction 34/55 and multiply by 360°, to get 222.5°. Since this is more than 180°, we should measure it in the opposite direction round the circle?or, equivalently, subtract it from 360°. The result is 137.5°, the value observed by the Bravais brothers.
The ratio of consecutive Fibonacci numbers gets closer and closer to the number 0.618034. For instance, 34/55?0.6182 which is already quite close. The limiting value is exactly (51/2-1)/2, the so-called golden number, often denoted by the Greek letter phi (F). Nature has left a clue for mathematical detectives: the angle between successive primordia is the "golden angle" of 360 (1- F)° = 137.5°. In 1907, G. Van Iterson followed up this clue and worked out what happens when you plot successive points on a tightly wound spiral separated by angles of 137.5°. Because of the way neighboring points align, the human eye picks out two families of interpenetrating spirals?one winding clockwise and the other counterclockwise. And because of the relation between Fibonacci numbers and the golden number, the numbers of spirals in the two families are consecutive Fibonacci numbers. Which Fibonacci numbers depends on the tightness of the spiral. How does that explain the numbers of petals? Basically, you get one petal at the outer edge of each spiral in just one of the families.
At any rate, it all boils down to explaining why successive primordia are separated by the golden angle: then everything else follows.
Douady and Couder found a dynamic explanation for the golden angle. They built their ideas upon an important insight of H. Vogel, dating from 1979. His theory is again a descriptive one--it concentrates on the geometry of the arrangement rather than on the dynamics that caused it. He performed numerical experiments which strongly suggested that if successive primordia are placed along the generative spiral using the golden angle, they will pack together most efficiently. For instance, suppose that, instead of the golden angle, you try a divergence angle of 90°, which divides 360° exactly. [ FIGURE S. omitted]
Then successive primordia are arranged along four radial lines forming a cross. In fact, if you use a divergence angle that is a rational multiple of 360°, you always get a system of radial lines. So there are gaps between the lines and the primordia don't pack efficiently. Conclusion: to fill the space efficiently, you need a divergence angle that is an irrational multiple of 360° multiply by a number that is not an exact fraction. But which irrational number? Numbers are either irrational or not, but like equality in George Orwell's Animal Farm, some are more irrational than others. Number theorists have long known that the most irrational number is the golden number. It is "badly approximable" by rational numbers, and if you quantify how badly, it's the worst of them all. Which, turning the argument on its head, means that a golden divergence angle should pack the primordia most closely. Vogel's computer experiments confirm this expectation but do not prove it with full logical rigor.
The most remarkable thing Douady and Couder did was to obtain the golden angle as a consequence of simple dynamics rather than to postulate it directly on grounds of efficient packing. They assumed that successive elements of some kind representing primordia form at equally spaced intervals of time somewhere on the rim of a small circle, representing the apex; and that these elements then migrate radially at some specified initial velocity. In addition, they assume that the elements repel each other like equal electric charges, or magnets with the same polarity. This ensures that the radial motion keeps going and that each new element appears as far as possible from its immediate predecessors. It's a good bet that such a system will satisfy Vogel's criterion of efficient packing, so you would expect the golden angle to show up of its own accord. And it does.
Douady and Couder performed an experiment not with plants, but using a circular dish full of silicone oil placed in a vertical magnetic field. They let tiny drops of magnetic fluid fall at regular intervals of time into the center of the dish. The drops were polarized by the magnetic field and repelled each other. They were given a boost in the radial direction by making the magnetic field stronger at the edge of the dish than it was in the middle. The patterns that appeared depended on how big the intervals between drops were; but a very prevalent pattern was one in which successive drops lay on a spiral with divergence angle very close to the golden angle, giving a sunflower-seed pattern of interlaced spirals, Douady and Couder also carried out computer calculations, with similar results. By both methods, they found that the divergence angle depends on the interval between drops according to a complicated branching pattern of wiggly curves. Each section of a curve between successive wiggles corresponds to a particular pair of numbers of spirals. The main branch is very close to a divergence angle of 137.5°, and along it you find all possible pairs of consecutive Fibonacci numbers, one after the other in numerical sequence. The gaps between branches represent "bifurcations," where the dynamics undergoes significant changes.
Of course, nobody is suggesting that botany is quite as perfectly mathematical as this model. In particular, in many plants the rate of appearance of primordia can speed up or slow down. In fact, changes in morphology, whether a given primordium becomes a leaf or a petal, say, often accompany such variations. So maybe what the genes do is affect the timing of the appearance of the primordia. But plants don't need their genes to tell them how to space their primordia: that's done by the dynamics. It's a partnership of physics and genetics, and you need both to understand what's happening.
Three examples, from very different parts of science. Each, in its own way, an eye-opener. Each a case study in the origins of nature's numbers the deep mathematical regularities that can be detected in natural forms. And there is a common thread, an even deeper message, buried within them. Not that nature is complicated. No, nature is, in its own subtle way, simple. However, those simplicities do not present themselves to us directly. Instead, nature leaves clues for the mathematical detectives to puzzle over. It's a fascinating game, even to a spectator. And it's an absolutely irresistible one if you are a mathematical Sherlock Holmes. (Nature's Numbers: The Unreality of Mathematical Imagination, Ian Stewart, Basic Books, New York 1995:135-143; emphases supplied. For further information see also The Fibonacci Numbers and Golden section in Nature - 1 and II )
Here once again we encounter the intermediate fibonacci pairings 34 and 55 discussed and applied in Part III with respect to planetary resonances, but underlying all of this is an undoubtedly complex relationship with natural growth, which returns us to Archytas with perhaps a slightly improved appreciation of the essence of the matter, specifically the imparting of an "organic motion to a geometric figure", i.e., as stated in the previous section, it was the latter who was:14
"The first who methodically applied the principles of mathematics to mechanics: who imparted an organic motion to a geometric figure, by the section of the semi-cylinder seeking two means that would be proportional, in order to double the cube."
But could this kind
of understanding have existed
that far back in time? Perhaps not, but then again, Ian Stewart's last
observation--that "nature leaves clues for the mathematical
detectives to puzzle
over"--is itself a most ancient one, as we
already
know from the two-part quotation from Ovid: "The three-fold
number
is present in all things whatsoever; nor did we ourselves discover this
number,
but rather nature teaches it to us" and the Chaldean Oracles ("for
the paternal Mind sowed Symbols through the World").
A.3.
THE
SPIRAL OF PHEIDIAS
In these modern times it
seems that we take Phi and the Phi-Series
largely
for granted. And we also perhaps fail to fully appreciate just how much
progress was made many decades (if not centuries) earlier as
illustrated
and recorded in works such as: On The Relation Of Phyllotaxis To
Mechanical
Law, by Arthur Harry Church (1904),15
by
Samuel Coleman and
Arthur C. Coan (Nature's Harmonic Unity, 1911 and Proportional
Form, 1920),16 Sir
Theodore Andrea Cook's
(The Curves
of Life, 1914),17 Sir
D'Arcy Wentworth
Thompson (On Growth
and Form, 1917, 1942)18 and
those listed
in R.C. Archibald's
Bibliography cited above. Interestingly enough, Cook also
includes
additional details concerning the name Phi and the
Phi-Series
by a Mr. William Schooling in the Introduction and Appendices
to The Curves of Life (1914). Here the dialogue includes "Phi"
itself,
Cook's treatment of "Man (as) the Measure of All Things",
Natural
Growth, Ideal Angles once again, and finally Mr. Mark Barr and William
Schooling's
Spiral of Pheidias:19
Mr. Mark Barr suggested to Mr. Schooling that his ratio should be called the Phi proportion for reasons given below.
The symbol Phi ( F )given to this proportion was chosen partly because it has a familiar sound to those who wrestle constantly with pi (the ratio of the circumference of a circle to its diameter), and partly because it is the first letter of the name of Pheidias, in whose sculpture this proportion is seen to prevail when the distances between salient points are measured. So much is this the case that the Phi proportion may be fitly called the "Ratio of Pheidias." Take a well-proportioned man 68 inches in height, or Phi 4. If we take ten inches as our unit of measurement. From the ground to his navel is 42 inches, or Phi 3 ; from his navel to the crown of his head is 26 inches, or Phi 2 ; from the crown of his head to the line of his breasts is 16 inches, Phi; and from his breasts to his navel is 10 inches, or the unit of measurements, or 1, which is Phi 0.
There are many valuable properties of Phi. Mr. Church, for instance, in pointing out the relation of spirally-constructed systems of plant growth to the Fibonacci ratio, speaks of the "Fibonacci or ideal angle" of 137° 30' 27.95". From what has been said above about the Phi proportion, it may be seen that this ideal angle can be prettily and neatly expressed in circular measurement as 2Pi/phi 2 (or twice Pi divided by the square of Phi).
I shall leave Mr. Schooling himself to explain many other most interesting facts concerning Phi in the Appendix. For the present it will be enough to say that it appears likely to give more accurate results for other forms of natural growth than the Fibonacci series so admirably used for botany by Mr. A.H. Church, and closer calculations in matters of art than the theory published in 1876 by Theodore Fechner in his "Vorschule der Aesthetik," I would further suggest that research into its uses in both directions would probably be well repaid; for in Mathematics it can be expressed with binomial coefficients, and it can also be used as a base which greatly facilitates the computation of logarithms. In Geometry and Trigonometry its properties are further explained in Appendix II (pp.441-447)

Fig. 2 The Pheidias Spiral
One more thing should be added here. If the radii vectores of a logarithmic spiral in Phi proportion, the result is not only a spiral of singularly pleasing character, but there is the further feature that on any radius the sum of the distances between two successive curves of the spiral equals the distance along the same radius to the succeeding curve (see Fig. 389). Such a Phi spiral bears a close resemblance shown in my second chapter produced by unwinding a tape from a shell (see Fig. 44, p.32).
In art, on the other hand, it ought to prove useful for proportional areas as for simple linear measurements; for since, as has been shown, the series is essentially spiral in character, and since it gives the Phi proportion along any radius, it should also it should also provide a formula for the proportions of successive areas or spaces between radii. I suggest that such increases of space as are observable in the various "compartments" of the shell shown in section in Fig.390, will be in Phi proportion, and bear a direct relation to the external spiral..... Mr. Schooling suspects (he does not claim yet to have proved) that the Phi proportion mentioned in the last chapter is an expression of economy of form, manifested in the packing of the human foetus, in the shape of shells, and in other ways. That such an economy of form should result in beauty is analogous with the fact that gracefulness is the result of ease or economy of force or effort....
Mr. Schooling also tells me that he is constructing an instrument for drawing logarithmic spirals automatically, using the Phi spiral as a standard, and stating the conditions of any other logarithmic spiral in terms of deviation from this standard. Incidentally this instrument will show that it is possible to proceed from a straight line to a circle through an infinite number of logarithmic spirals. T.A.C 1914 .
(Appendix I. Nature and Mathematics, Sir Theodore Andrea Cook, The Curves of Life, 1914:440; for clarity the word "Phi" has been substituted for the corresponding symbol in Cook's exposition of "Man as the Measure of all Things").
The "historical" establishment of the name "Phi" is of interest here, although it is not necessarily exclusive, and there are also a number of other interesting points raised. Nevertheless--Anaxagoras notwithstanding--it seems fair to suggest that not all would necessarily agree with Sir Theodore Andrea Cook's application of Phi to the human form, especially since his example of a "well-proportioned man 68 inches in height" makes little allowance for the considerable variations in girth and height that routinely occur among members of the human race. Putting it another way, it is not at all certain--Ovid's "Natural" Three-fold number notwithstanding--that the constant Phi would be immediately apparent if the matter was actually put to the test among the general population. Far better suited to this purpose would be the many spiral forms in nature already addressed by Cook himself, especially, it would seem, those prominently exhibited among certain shells--"Golden"-- or otherwise. Thus Cook is on firmer ground with his Phi-related assignments regarding the latter and also the other aspects of his extensive analyses. As is Samuel Coleman in Nature's Harmonic Unity, a work in progress unknown to Cook (and vice-versa) that was published three years earlier than Cook's Curves of Life (1914). By way of an introduction to both, the part of the Appendix to Theodore Andreas Cook's The Curves of Life published in 1914 that records his surprise, reception and criticism of Samuel Coleman's Nature's Harmonic Unity is given below:19
JUST as I was reading the proofs of "The Curves of Life," a book by Samuel Coleman, M.A., edited by C. Arthur Coan, LL.B., and published by Messrs. G. P. Putnam's Sons, was sent to me from New York, entitled "Nature's Harmonic Unity: A Treatise on its Relation to Proportional Form." Its preface is dated December 1st, 1911, and it therefore provides a very interesting example of the way in which two minds may be attracted by kindred subjects at the same time, without any knowledge of each other's studies, and arrive at different conclusions from a similar set of data. Readers of the Field in 1912 will remember the chapters in that paper in which I tried to expound certain principles which are discoverable in natural growth, and applied them to such artistic creations as the Parthenon and the Open Staircase of Blois, illustrating my theory from a large number of examples chosen from botany, anatomy, conchology, and other branches of natural science. A great many such" illustrations" of his thesis are provided by Mr. Coleman in the volume before us, from the nautilus or the sunflower, to the Parthenon or the facade of Rheims Cathedral. Yet the treatment and main result are different. Although Mr. Coleman's pages and Mr. Coan's mathematics are of absorbing interest, I venture to uphold the theory set forth in 1912 in the Field and developed in "The Curves of Life" as a better working hypothesis, a better "explanation" of the phenomena.
The title of Mr. Coleman's book suggests and epitomises the contrast between his attitude and mine. I could almost call my book Nature's Geometrical Diversity in contrast with Mr. Coleman's Nature's Harmonic Unity. There is some confusion also in his use of the word "unity." At one time he seems to suggest that the phenomena of Nature and art exhibit the common characteristic--the one feature--of obedience to the laws of Nature, which is true. Elsewhere, and in the main, he insists that these varied phenomena exhibit unity by following one--and only one law--so far as proportion of form is concerned. The expression of that law he finds mainly in "extreme and mean proportion." He regards deviations from this law as negligible, and it is even suggested that, since the measurements of the Parthenon do not conform precisely with this law, the measurements are wrong! I hold, on the contrary, that the deviations from law are of more moment and of greater interest; that they are better calculated to extend our knowledge than the detection of rigid conformity with the law.
Again, his book is concerned with proportional form, while I think that far greater advantages attach to considering form in connection with growth. He may be said to be dealing with morphology apart from physiology, with form separate from function, whereas, in my judgment, considerations of function and growth are essential to the right understanding of form and its proportion. He proposes to explain the complicated phenomena of forms in life and of beauty in art by saying that they all agree with one very simple mathematical expression. My position, on the contrary, is that the phenomena of. life and beauty are always accompanied by deviations from any simple mathematical expression we can at present formulate.
Mathematics, to my mind, are of the highest value as an instrument; but, as we have seen in previous pages, it is of the essence of a living thing, as of a beautiful work of art, that it cannot be exactly defined by any simple mathematical formula like that chosen by Mr. Coleman. I have pointed out in the last chapter that the agreement of a number of phenomena with a given formula is not an important factor in knowledge; it merely sums up a certain sphere of investigation in a convenient way. The really important thing is the exception. But I must not be taken as expressing disdain for laws in general or for Mr. Coleman's mathematics in particular. Indeed, without the mathematical expression as a guide we should be unable to take note right of the aberration, and to this extent Mr. Coleman and Mr. Coan have done very valuable work; but Mr. Coleman makes, as I think, the fundamental error (which runs through his whole argument) of predicating certain mathematical forms in his own mind, and then saying that they exist in the natural object (still more in the artificial or architectural object) which he is examining. Judging it on these lines, the most valuable part of Mr. Coleman's book is to be found in Mr. Coan's appendix, which faithfully and accurately sets out the actual differences between living organisms (or architectural creations), and strictly mathematical results. It is these differences which predicate life in the one case and beauty in the other. . . .
. . . .Mr. Coleman shows ordered proportions which may be attributed to certain laws. But he sees too much in laws when he means by this word the narrowest sort of geometrical relations. The law of extreme and mean proportion stands out as a proved principle, and it does govern a pleasant relation for the sweep of the eye across some architectural and natural spacings. It is the old and well-known "Golden Section." It is also Euclid, Book VI., prop. 30. But this principle is not more than a letter in the alphabet of architecture, to say nothing of the other arts. Mr. Coleman (guided, I think, too little by his editor) believes not only in a very wide application of the Golden Section, but he wishes to show that most of art is governed either by this or by other laws which are as easily formulated. In order to prove his contention, he draws a maze of lines over hi architecture and his natural objects (as may be seen from those hen reproduced), but the lines result merely in presenting one or another aspect of the extreme and mean proportion. And while no one can deny that this relation is important, the author tries to show too much more than Zeising and Fechner showed. Still, it would be unfair to overlook the author's extension of the older observations, and one is surprised to see the increased number of agreements with ordered geometry. But when we analyse the geometry we find that the author's demonstrations could be expressed by a very simple formulation of the wider meanings of the extreme and mean proportion. Such a simplified formulation at once exposes the improbability of a royal road to the arts, though it widens the significance of the Golden Section.
(Cook, 1914: 431-441; the cited examples of Samuel Coleman's graphical treatments are omitted here for brevity)
It could be said that in places Cook is perhaps somewhat harsh in his criticism, yet in presenting his own viewpoint he nevertheless also provides publicity and permanent linkage to Coleman's work, and moreover, he also seems to have taken pains to include the more easily absorbed diagrams produced by the latter. These two works with their obvious similarities and differences were soon after followed by Sir D'Arcy Wentworth Thompson's massive On Growth and Form in 1917--a treatise that included an extended technical analysis of spiral configurations in general and in particular as applied to shells. Here again, if there was ever a subject where Ovid's "Three-Fold Number" was evident with respect to structure and form, thus must surely have been it, as a number of investigators appear to have realized well before Cook and Coleman, who nevertheless noted in Chapter IX ("On Conchology") in Nature's Harmonic Unity (1911):20
Mr. T. A. Cook, in his excellent book entitled Spirals in Nature and Art, declares that: 'If any particular class of objects should be chosen by a student for purposes of study in relation to so mathematical and creative an art as architecture, the class of shells would be most suitable inasmuch as they suggest with particular emphasis those structural and mathematical problems the builder has to face."
It is not the intention
here to indulge in comparitive analyses per se, or comment
extensively
on either works, but rather emphasize once again that the present
treatment
approaches such topics from a somewhat different direction. So much so,
if
fact, that it is possible to approach the subject of spiral formations
pre-equipped
with an array of accurate, pre-determined spirals. This is in marked
contrast
(apart from William Schooling's mechanical device) to most earlier
methods
employed to classify spirals that occur in nature--all of which
necessarily
required some form of detailed measurement and subsequent analysis. The
difficulty with the latter is obvious enough, for natural spirals not
only exhibit
growth, but also along the way incorporate initial, intermediate and
final
stages in their formation. And while such spirals may well have
distinctly
characteristic spirals and therefore "characteristic numbers" (as
applied
to shells by Canon Mosely in 1838), there still remain deviations from
both
the base spiral and the theoretically perfect. Where then, does one
draw
the line and reject variations in measured data? And how does one
handle
the tighter spirals with their minimal separations? Then again, what if
observed
variations are of significance in their own right in certain
situations--as
indeed they might well be?
This last question was in fact taken up by Sir Theodore
Andrea Cook, who also wrote in the Appendix to The Curves of Life:
21
If there be, as I think there is, a tendency for a nautilus to acquire the form of a logarithmic spiral, just as there is a tendency for a book to fall under the action of gravity, and yet there is no known example of a nautilus shell being an exact logarithmic spiral, it is reasonable to assume that there are other forces at work, akin to friction or muscular action, which cause this deviation. The deviation stimulates us to further investigation, and to the probable or possible discovery of some other law of nature, from which in turn deviations will be discovered, leading to yet further extension of knowledge.
If "exact" is taken to be synonymous with perfect, then Cook is undoubtedly correct, even with respect to the nautilus, whose spiral can nevertheless be closely approximated by an equiangular spiral with a growth factor of approximately 3 (see the next section for a more accurate value), but with due caution nevertheless since the fitting of two-dimensional spirals to natural objects is a complex matter requiring precise definition.
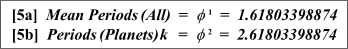

Fig. 3 The Pheidias Spiral and Spira Solaris
A study of the relative sizes and degrees of "opening" for a wide range of "Nautiloid Spirals" was undertaken by Sir D'Arcy Wentworth Thompson starting with a small growth factor of 1.1 : 1 (corresponding angle 89;08 degrees) and 21 increasing values, ending with a growth factor of 1,000,000,000 : 1 (corresponding angle less than 19 degrees). Commenting on these results Sir D'Arcy Wentworth Thompson explained further: 22
We see that with smaller angles the apparent form of the spiral is greatly altered, and the very fact of its being a spiral soon ceases to be apparent (Figs. 379, 380). Suppose one whorl to be an inch in breadth, then, if the angle of the spiral were 80°, the next whorl would (as we have just seen) be about three inches broad; if it were 70°, the next whorl would be nearly ten inches, and if it were 60°, the next whorl would be nearly four feet broad. If the angle were 28°, the next whorl would be a mile and a half in breadth; and if it were 17°, the next would be some 15,000 miles broad. (Sir D'Arcy Wentworth Thompson, On Growth and Form, New York 1992:792; unabridged reprint of the 1942 edition)
This is helpful and
informative enough, but initially it may still be difficult to grasp
the inter-relationship between the growth factor and the equiangular
form of the associated spirals. The reason for this is perhaps more
subtle than one might think, at least initially. One might note, for
example, that the innermost part of Schooling's original Pheidias
Spiral does not commence at zero, but starts some distance from it. In
fact when generating equiangular spirals this consideration
can pose technical problems, especially with spirals having relatively
small
exponents and near-circular configurations (e.g., Phi 1/6
with
a growth factor of 1.083505882 : 1). Then again, if we
are to take our cues from Nature we might also emulate the construction
priorities of the spider, starting instead from the outside and
working inward, but more on this intriguing aspect in the next
section.
Closely allied to the initialization problem, however, is
the more general question of how in this context one actually measures
exponential growth in the first place. The increase in growth is, of
course, a fixed ratio, and for the Pheidias spiral the
ratio, as we already know, is 1.61803398874 : 1.
But is it immediately apparent
from Fig.2 that this is so for the Pheidias spiral throughout--above,
below,
and in all directions whatsoever? Probably not. What is likely required
is
more definition, in fact the type of precision that Sir Theodore Andrea
Cook
had already provided a little earlier in The Curves of Life. Why
then
present his material out of order here? Because it is not quite that
simple,
that's why. And, as the reader will soon find out, in gaining a better
understanding of the equiangular spiral, it also becomes possible to
appreciate more fully precisely what it was that Sir Theodore Andrea
Cook imparted along the way.
A.4:
THE
EQUIANGULAR SPIRAL AND THE ELEMENTS
What follows next remains
something of a puzzle at present. According to the source (Sir Theodore
Andrea Cook) a certain degree of progress appears to have been made
relating the equiangular spiral to the chemical elements, though little
awareness of this particular application apparently remains today, at
least in the general literature. Nevertheless, under the title FINAL
RESULTS in The Curves of Life Cook recounts (in 1914) that:23
In 1888 Dr. Johnstone Stoney submitted to the Royal Society a memoir on the"logarithmic law of atomic weights," which, however, was not published in full. Lord Raleigh (Proceedings of the Royal Society, Series A, Vol. LXXXV., p. 471, 1911) consulted the original manuscript, and gives some extracts from and remarks upon it. After many fruitless efforts to extract information from the curves obtained by plotting the atomic weights, it happily occurred to Dr. Stoney to employ the volumes proportioned to the atomic weights. When this was done the resulting figure (cf. Fig. 385) at once suggested a well-known logarithmic spiral, and a close scrutiny justified this suspicion. In other words, the relations of all the known elements to each other could almost exactly be expressed by the logarithmic spiral. If this held true of what was known already, it became apparent that it would also hold true of what was to be discovered later on; and that if new elements were discovered after 1888, they would find their right places in the gapes indicated in Dr. Johnstone Stoney's spiral diagram. This remarkable process had already occurred in Mendeléef's Periodic System since the year of its publication in 1869: and the fact that it has also occurred in the spiral system (which includes the Mendeléef System and gives it additional confirmation) is one of the most convincing proofs that the spiral system is not merely a correct hypothesis, but a fundamental law. The total of the elements known in 1912 was about eighty-three. Six elements were missing in 1888 in Dr. Stoney's diagram, between hydrogen and lithium; Sir William Ramsay discovered helium in 1895, which fills one of the gaps, though the position is not mathematically exact. But on the sixteenth radius an even more remarkable corroboration was effected, in what had hitherto been a gap between the most intensely electro-negative elements (such as fluorine, chlorine, bromine, and iodine) and the most electro-positive elements (such as lithium, sodium, potassium, etc.). This gap was filled with absolute appropriateness, by the series of inert gases: argon, discovered by Lord Raleigh, and Sir William Ramsay in 1894, and helium, neon, krypton, and xenon, discovered by Sir William Ramsay between 1895 and 1898, five new elements which occupy places foretold to be necessary to the Mendeléef series as well.
(Theodore Andrea Cook, The Curves of Life, Dover, New York, 1978:413; republication of the London (1914) edition.
Although the latter part is dated in any case, the puzzle concerns not only the fact that in spite of its potential importance Dr. Johnstone Stoney's paper was "not published in full," but also Cook's resulting figure (Fig. 385) which though undefined is apparently "a well-known logarithmic spiral" -- a conclusion reinforced moreover, by "close scrutiny" that apparently "justified this suspicion." Thus the impression gained here is that this was not simply the well-known logarithmic spiral under consideration at all, but something altogether more specific that for some reason nevertheless remained undefined. On the following page, however, Cook returns to Dr. Johnstone Stoney's "resulting figure" (i.e., the above mentioned Fig. 385) to demonstrate the concept of growth "along radii" as follows:24
In mathematics we have the most supple and beautifully precise instrument by which the human mind can fulfil its need of cataloguing, labelling, defining the multifarious facts of life around us. In this task the visible expression of various results or totals in the form of curves is an invaluable convention; and the problems of growth or increase the logarithmic spiral occupies perhaps the most important position of all. For it can be used not merely in the sense of the curve of growth an energy, which swings from origin to outer space, it can define growth along its radii as well.

In Fig. 385, for instance, we have the definite curve which has grown from the centre we will call C to B, and ends (as far as I have drawn it) at A. But we have also the radii which I will call CP, CL, CM, CN, each of which is cut at three points by the curve progressing from C to A, and you will notice that the three points of intersection on the line CP are differently situated (with regard to C) from the points of intersection on CL, which differs again, in this respect, from CM, and CM differs from CN. Now, since the spiral curve CBA extends infinitely in each direction from any point within it, which is easier to imagine at A than it is at C, and since there can be any number of radii, so this mathematical concept embodies the great truth of infinite gradations, which is explained in the very beautiful and valuable theory of infinite series. The rhythmical beat of the spiral curve upon its radii is in direct relation to this theory, as has been pointed out to me by Mr. Mark Burr. (Theodore Andrea Cook, The Curves of Life, Dover, New York, 1914:414)

Fig. 385B Extended

Thus we appear to have a specific logarithmic spiral relating to the chemical elements ca 1888 as recorded in a 1914 publication. But how could something this fundamental have been ignored and/or allowed to simply fade away? Were there problems with the analysis, perhaps? Was it subsequently proved erroneous? Or (although unlikely), was the spiral in question simply coincidental? Who knows, and this is indeed a puzzle--one that increases yet again in light of the subsequent (and quite recent) application of the spiral form in the discovery of the molecule "buckminsterfullerene." Moreover, Hugh Aldersey-Williams, in describing the investigations leading up to the latter discovery mentions the perhaps surprising (and perhaps not so surprising) role played by Sir D'Arcy Wentworth Thompson along the way:25
Thompson's claim to fame rests largely on one extended and luminous essay, On growth and form; it is this work that is cited by the Rice group. The contemporary palaeontologist and author Stephen Jay Gould has called Thompson "perhaps the greatest polymath of our century" and his essay "one of the great lights of science and of English prose, the greatest work of prose in twentieth-century science". Thompson's aim was to show that the shape of living things has a mathematical basis (and hence has no need for reliance on supernatural or teleological explanation). His argument is completely general. It applies to plants and animals, to airborne, waterborne, and land creatures of all sizes. He notes that the Eiffel Tower and John Smeaton's design for the Eddystone lighthouse both take the form of the trunk of an oak tree. It would be easy to conclude that nature inspired man to create these shapes. But it would be more perceptive to note, as Thompson did, that both man and nature take the most economical course of action prescribed by physical laws.
.......
Polymath though he was, D'Arcy Thompson had little to say about chemistry. Nevertheless, he was to serve Kroto and Smalley's purpose as rather more than just an erudite ambassador for Euler's theorem. His genius can be seen as an inspiration behind a beautiful diagram in the paper on the reactivity of the fullerenes which shows a buckminsterfullerene molecule encased inside a larger spheroidal carbon frame, which in turn is beginning to be enclosed by a third shell. The whole spiral scheme bears a remarkable resemblance to the spiral pattern of growth adopted by some plants and animals that are illustrated in Thompson's book. (The resemblance is in fact a little misleading. As Thomson points out, nature favours the "equiangular or logarithmic" spiral which a radius drawn from the centre of the spiral to its leading edge increases in geometric progression - that is, by a constant factor - as sucessive orbits are scribed out. This is the mathematical relationship followed by the Nautilus sea-shell and many other gastropods. In the alternative, the "equable" or Archimedean spiral, this radius increases in roughly arithmetic progression - that is, by a constant increment - generating a spiral like that of a Swiss roll or a coiled rope. It is this latter model that lies at the heart of the proposed mechanism for the growth of soot particles, the spacing of successive layers being not the thickness of a piece of sponge cake or the diameter of a rope but the familiar van der Waals distance between layers of graphite.) (Hugh Aldersey-Williams, THE MOST BEAUTIFUL MOLECULE: THE DISCOVERY OF THE BUCKYBALL, John Wiley & Sons, New York 1995:113-114)
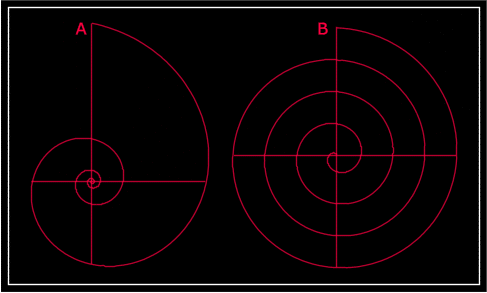
Fig. 3a The Equiangular Spiral Phi e Fig. 13 The "Archimedian" (Log) Spiral Phi e

Fig. 4a. Relations
14a-14e and the Ideal Growth Angle

Fig.
4b. Varying Velocity: The Jupiter-Saturn Synodic Cycle SD1
The
three associated periods (the sideral period of Saturn, the
Jupiter-Saturn
Synodic cycle SD1,
and the sidereal period of Jupiter) also, of course, provide the most
obvious and
best known fibonacci resonances in the Solar System, i.e., the 2
: 3 : 5 60-year cycle (see Part III for details and other
expansions).
Additionally,
as treated further in
the following section, angular momentum (L) may be
obtained from the product
of the planetary mass and the inverse orbital velocity.
The latter, for the Phi-Series Jupiter-Saturn Synodic cycle
is once again the primary period constant, i.e., Phi 2
=
2.61803398, albeit in a different application; see Part
IVb2c: The
Pheidian Planorbidae for the final details and conclusions.
Lastly, it is invariably stated that one of the equiangular spiral's more unusual properties is that "the invert to an equiangular spiral is identical with the original curve," also described by D'arcy Wentworth Thompson (1942:767) as:
one of the most beautiful and most singular properties of the curve. It was this which led James Bernoulli, in imitation of Archimedes, to have the logarithmic spiral inscribed upon his tomb; and on John Goodsir's grave near Edinburgh the same symbol is reinscribed.
Nevertheless, the two equiangular spirals under consideration--Spira Solaris ( Phi 2 = 2.61803398 shown below in red and its inverse Phi -2 = 0.381966011 in blue)--would appear to possess a difference in phase, i.e., identical plots incorporating 360 data points per revolution over six revolutions (2160 data points for k = Phi 2 and k = Phi -2 respectively) actually produce the following result:
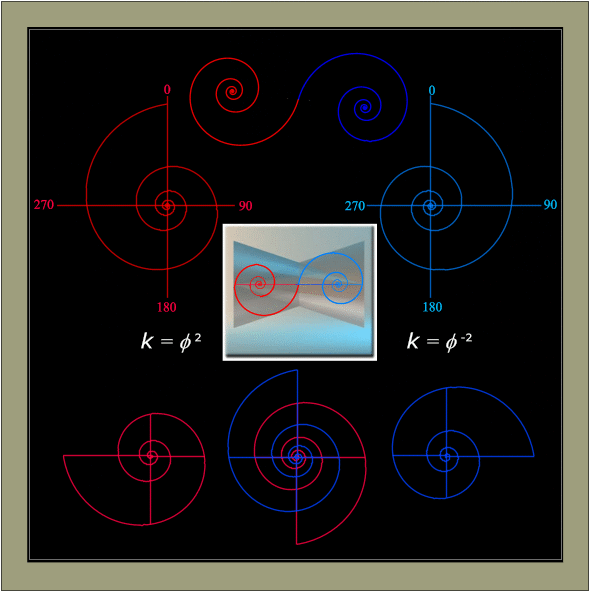
Fig. 4c. The
Equiangular Spirals k = Phi 2, Phi -2
and Gyres
A.6.
BENJAMIN PIERCE, LOUIS AGASSIZ, FIBONACCI, AND THE SOLAR
SYSTEM
It may well be that the extension of the "Three-fold Number"
beyond terrestrial boundaries is simply the logical continuation of
Ovid's initial observation that "The three-fold number is present in
all things whatsoever" --an observation that in view of the nature
of spiral galaxies need not remain with planetary systems per se.
Nevertheless, the linking of natural growth to the structure of
planetary systems was undoubtedly a bold and momentous step even though
it also reflects the second part of the quotation from Ovid: "Nor
did we ourselves discover this number, but rather
natures teaches it to us." At least this seems applicable in
the
case of Benjamin Peirce,26 who integrated
both to successfully apply the Fibonacci series to the structure of the
Solar System. The latter's work was originally published in the Proceedings
of the AAAS in 1850 and given additional permanence with a further
airing in Louis Agassiz's Essay
on Classification in 185727. All to
little or no avail,
it would seem, for in spite of the details and the implications the
work
it still remains in relative obscurity to the present day. In some
respects
this may be understandable, though the subsequent lack of attention or
acceptance
can hardly be blamed on the quality of the work or the means of
presentation.
All too easily dismissed as "speculative biology" (Lurie 1962:128)
28 it would seem, it is likely that
it was also one of the first victims of
"Bode's "Law" which first surfaced less than a decade later (1866-1871)
despite
its fatal mathematical flaws and ad hoc origins. Indeed,
if
longevity and popularity alone provide the guidelines, then "Bode's
Law"
would win hands-down in any comparison between the two planetary
frameworks.
If, however, the standard by which such matters are judged depends not
on
popularity or elementary mathematics, but on human progress and
increased
understanding, then one can only wonder what else might have been
accomplished
since Agassiz's time and sadly lament the loss.
The
complete description of Benjamin Pierce's application of the Fibonacci
series to
the structure of the Solar System as published by Louis Aggassiz is
provided
below; perhaps significantly, the words "Fibonacci" and/or the "Golden
Section"
(and the like) are noticeably absent--such words perhaps already
unacceptable
to the powers that be and also a perceived threat to the status quo.
Nevertheless, there can be no mistaking the sequence applied or the
major
premise, called here perhaps fittingly enough (for the moderns, at
least)
"the law of phyllotaxis". One may also note that Peirce had already
considered
the practical differences between his theoretical treatment and the
Solar
System itself and subsequently considered not only the position of
Earth,
but also discepancies encountered for the positions of Mars, Uranus and
Neptune.
Initially Pierce also applied a double form of Fibonacci series but
subsequently
reduced the set to arrive are a situation similar to that involving the
synodic
difference cycle between adjacent planets.
ESSAY ON CLASSIFICATION
Louis Agassiz 1857
FUNDAMENTAL RELATIONS OF ANIMALS
SECTION XXXI
COMBINATIONS IN TIME AND SPACE OF VARIOUS KINDS OF RELATIONS AMONG ANIMALS
It must occur to every reflecting mind, that the mutual relation and respective parallelism of so many structural, embryonic, geological, and geographical characteristics of the animal kingdom are the most conclusive proof that they were ordained by a reflective mind, while they present at the same time the side of nature most accessible to our intelligence, when seeking to penetrate the relations between finite beings and the cause of their existence.
The phenomena of the inorganic world are all simple, when compared to those of the organic world. There is not one of the great physical agents, electricity, magnetism, heat, light, or chemical affinity, which exhibits in its sphere as complicated phenomena as the simplest organized beings; and we need not look for the highest among the latter to find them presenting the same physical phenomena as are manifested in the material world, besides those which are exclusively peculiar to them. When then organized beings include everything the material world contains and a great deal more that is peculiarly their own, how could they be produced by physical causes, and how can the physicists, acquainted with the laws of the material world and who acknowledge that these laws must have been established at the beginning, overlook that à fortiori the more complicated laws which regulate the organic world, of the existence of which there is no trace for a long period upon the surface of the earth, must have been established later and successively at the time of the creation of the successive types of animals and plants?
Thus far we have been considering chiefly the contrasts existing between the organic and inorganic worlds. At this stage of our investigation it may not be out of place to take a glance at some of the coincidences which may be traced between them, especially as they afford direct evidence that the physical world has been ordained in conformity with laws which obtain also among living beings, and disclose in both spheres equally plainly the workings of a reflective mind. It is well known that the arrangement of the leaves in plants148 may be expressed by very simple series of fractions, all of which are gradual approximations to, or the natural means between 1/2 or 1/3, which two fractions are themselves the maximum and the minimum divergence between two single successive leaves. The normal series of fractions which expresses the various combinations most frequently observed among the leaves of plants is as follows: 1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, 21/55, etc. Now upon comparing this arrangement of the leaves in plants with the revolutions of the members of our solar system, Peirce has discovered the most perfect identity between the fundamental laws which regulate both, as may be at once seen by the following diagram, in which the first column gives the names of the planets, the second column indicates the actual time of revolution of the successive planets, expressed in days; the third column, the successive times of revolution of the planets, which are derived from the hypothesis that each time of revolution should have a ratio to those upon each side of it, which shall be one of the ratios of the law of phyllotaxis; and the fourth column, finally, gives the normal series of fractions expressing the law of the phyllotaxis.149
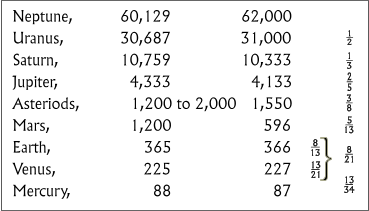
Table I (Agassiz-Pierce 1857)In this series the Earth forms a break; but this apparent irregularity admits of an easy explanation. The fractions: 1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, etc., as expressing the position of successive leaves upon an axis, by the short way of ascent along the spiral, are identical as far as their meaning is concerned with the fractions expressing these same positions by the long way, namely, 1/2,2/3, 3/5, 8/13, 13/21, 21/34, etc.
Let us therefore repeat our diagram in another form, the third column giving the theoretical time of revolution.

Table II (Agassiz-Pierce 1857)It appears from this table that two intervals usually elapse between two successive planets, so that the normal order of actual fractions, 1/2, 1/3, 2/5, 3/8, 5/13, etc.,or the fractions by the short way in phyllotaxis, from which, however, the Earth is excluded, while it forms a member of the series by the long way. The explanation of this, suggested by Peirce, is that although the tendency to set off a planet is not sufficient at the end of a single interval, it becomes so strong near the end of the second interval that the planet is found exterior to the limit of this second interval. Thus, Uranus is rather too far from the Sun relatively to Neptune, Saturn relatively to Uranus, and Jupiter relatively to Saturn; and the planets thus formed engross too large a proportionate share of material, and this is especially the case with Jupiter. Hence, when we come to the Asteroids, the disposition is so strong at the end of a single interval, that the outer Asteroid is but just within this interval, and the whole material of the Asteroids is dispersed in separate masses over a wide space, instead of being concentrated into a single planet. A consequence of this dispersion of the forming agents is that a small proportionate material is absorbed into the Asteroids. Hence, Mars is ready for formation so far exterior to its true place, that when the next interval elapses the residual force becomes strong enough to form the Earth, after which the normal law is resumed without any further disturbance. Under this law there can be no planet exterior to Neptune, but there may be one interior to Mercury.
Let us now look back upon some of the leading features alluded to before, omitting the simpler relations of organized beings to the world around, or those of individuals to individuals, to consider only the different parallel series we have been comparing when showing that in their respective great types the phenomena of animal life correspond to one another, whether we compare their rank as determined by structural complication with the phases of their growth, or with their succession in past geological ages; whether we compare this succession with their embryonic growth, or all these different relations with each other and with the geographical distribution of animals upon earth. The same series everywhere! These facts are true of all the great divisions of the animal kingdom, so far as we have pursued the investigation; and though, for want of materials, the train of evidence is incomplete in some instances, yet we have proof enough for the establishment of this law of a universal correspondence in all the leading features which binds all organized beings of all times into one great system, intellectually and intelligibly linked together, even where some links of the chain are missing. It requires considerable familiarity with the subject even to keep in mind the evidence, for, though yet imperfectly understood, it is the most brilliant result of the combined intellectual efforts of hundreds of investigators during half a century. The connection, however, between the facts, it is easily seen, is only intellectual; and implies therefore the agency of Intellect as its first cause.150
And if the power of thinking connectedly is the privilege of cultivated minds only; if the power of combining different thoughts and of drawing from them new thoughts is a still rarer privilege of a few superior minds; if the ability to trace simultaneously several trains of thought is such an extraordinary gift, that the few cases in which evidence of this kind has been presented have become a [p.131] matter of historical record (Caesar dictating several letters at the time), though they exhibit only the capacity of passing rapidly, in quick succession, from one topic to another, while keeping the connecting thread of several parallel thoughts: if all this is only possible for the highest intellectual powers, shall we by any false argumentation allow ourselves to deny the intervention of a Supreme Intellect in calling into existence combinations in nature, by the side of which all human conceptions are child's play?
If I have succeeded, even very imperfectly, in showing that the various relations observed between animals and the physical world, as well as between themselves, exhibit thought, it follows that the whole has an Intelligent Author; and it may not be out of place to attempt to point out, as far as possible, the difference there may be between Divine thinking and human thought. Taking nature as exhibiting thought for my guide, it appears to me that while human thought is consecutive, Divine thought is simultaneous, embracing at the same time and forever, in the past, the present, and the future, the most diversified relations among hundreds of thousands of organized beings, each of which may present complications again, which, to study and understand even imperfectly, as for instance, Man himself, Mankind has already spent thousands of years. And yet, all this has been done by one Mind, must be the work of one Mind only, of Him before whom Man can only bow in grateful acknowledgment of the prerogatives he is allowed to enjoy in this world, not to speak of the promises of a future life.
I have intentionally dismissed many points in my argument with mere questions, in order not to extend unduly a discussion which is after all only accessory to the plan of my work. I have felt justified in doing so because, from the point of view under which my subject is treated, those questions find a natural solution which must present itself to every reader. We know what the intellect of Man may originate, we know its creative power, its power of combination, of foresight, of analysis, of concentration; we are, therefore, prepared to recognize a similar action emanating from a Supreme Intelligence to a boundless extent. We need therefore not even attempt to show that such an Intellect may have originated all the Universe contains; it is enough to demonstrate that the constitution of the physical world and, more particularly, the organization of living beings in their connection with the physical world, prove in general the existence of a Supreme Being as the Author of all things. The task of science is rather to investigate what has been done, to inquire if possible how it has been done, than to ask what is possible for the Deity, as we can know that only by what actually exists. To attack such a position, those who would deny the intervention in nature of a creative mind must show that the cause to which they refer the origin of finite beings is by its nature a possible cause, which cannot be denied of a being endowed with the attributes we recognize in God. Our task is therefore completed as soon as we have proved His existence. It would nevertheless be highly desirable that every naturalist who has arrived at similar conclusions should go over the subject anew from his point of view and with particular reference to the special field of his investigations; for so only can the whole evidence be brought out. I foresee already that some of the most striking illustrations may be drawn from the morphology of the vegetable kingdom, especially from the characteristic succession and systematical combination of different kinds of leaves in the formation of the foliage and the flowers of so many plants, all of which end their development by the production of an endless variety of fruits. The inorganic world, "considered in the same light, would not fail to exhibit also unexpected evidence of thought, in the character of the laws regulating the chemical combinations, the action of physical forces, the universal attraction, etc., etc. Even the history of human culture ought to be investigated from this point of view. But I must leave it to abler hands to discuss such topics.
SECTION XXXI
RECAPITULATION
Last Section (31st)
31st. The combination in time and space of all these thoughtful conceptions exhibits not only thought, it shows also premeditation, power, wisdom, greatness, prescience, omniscience, providence. In one word, all these facts in their natural connection proclaim aloud the One God, whom man may know, adore, and love; and Natural History must in good time become the analysis of the thoughts of the Creator of the Universe, as manifested in the animal and vegetable kingdoms, as well as in the inorganic world.
It may appear strange that I should have included the preceding disquisition under the title of an "Essay on Classification." Yet it has been done deliberately. In the beginning of this chapter I have already stated that Classification seems to me to rest upon too narrow a foundation when it is chiefly based upon structure. Animals are linked together as closely by their mode of development, by their relative standing in their respective classes, by the order in which they have made their appearance upon earth, by their geographical distribution, and generally by their connection with the world in which they live, as by their anatomy. All these relations should therefore be fully expressed in a natural classification; and though structure furnishes the most direct indication of some of these relations, always appreciable under every circumstance, other considerations should not be neglected which may complete our insight into the general plan of creation. (Louis Agassiz, ESSAY ON CLASSIFICATION, Ed. E. Lurie, Belknap Press, Cambridge, 1962:127-128)
As far as Pierce's still largely unheralded contribution and its attempted furtherance by Louis Agassiz are concerned one might note that although the latter gives due prominence to the subject in his Essay on Classification this highly significant issue is still rarely mentioned in abstracts or notes on the latter's work itself. Yet the understanding inherent in the basic premise was hardly likely to have been entirely isolated, as Agassiz himself stresses in the following passage, which also carries with it familiar yet ancient echoes of unity and applied intellect:29
These facts are true of all the great divisions of the animal kingdom, so far as we have pursued the investigation; and though, for want of materials, the train of evidence is incomplete in some instances, yet we have proof enough for the establishment of this law of a universal correspondence in all the leading features which binds all organized beings of all times into one great system, intellectually and intelligibly linked together, even where some links of the chain are missing. It requires considerable familiarity with the subject even to keep in mind the evidence, for, though yet imperfectly understood, it is the most brilliant result of the combined intellectual efforts of hundreds of investigators during half a century. The connection, however, between the facts, it is easily seen, is only intellectual; and implies therefore the agency of Intellect as its first cause
One major difference between this approach and others lies in the direction used by Peirce; i.e., the latter commenced from the outermost regions and applied Fibonacci-related divisions while moving inwards towards the center. Here the location of Neptune was perhaps a key (or a hindrance) in that the secondary position (i.e., the synodic location of the exponential framework) happens to be similar to that of Neptune itself. On the other hand, however, the 1 : 1 occurrence was perhaps--rightly or wrongly--also an alerting factor for the Fibonacci series itself. Nor should this necessarily matter, for the premise itself was already absorbed and applied.
In retrospect it is hard to say how far this line of inquiry might have been taken, or what might ultimately have resulted, but it must surely have been a far more useful endevour than the circular, simplistic and ad hoc diversions introduced and perpetuated by "Bode's Law." And how could something so momentous and far-reaching have been so easily driven into obscurity? According to the modern editor of Agassiz' Essay on Classification, (E. Lurie) it was partly the work of Asa Gray and Chauncey Wright, as explained in the following footnote (the latter's No.149):30
Agassiz tried to interest Americans in this concept, an idea typical of German speculative biology and one that he had been much impressed with since his student days at the University of Munich. See Asa Gray, "On the Composition of the Plant by Phytons, and Some Applications of Phyllotaxis," Proceedings, AAAS, II (1850), 438-444, and Benjamin Peirce, "Mathematical Investigations of the Fractions Which Occur in Phyllotaxis," in ibid., 444-447. Gray was never entirely convinced of the validity of this ideal conception. He subsequently encouraged Chauncey Wright to examine the problem of leaf arrangement, with the result that such facts were shown to be understandable in terms of the principle of natural selection.
but it is still incredible
that it should have been driven down so swiftly, except, perhaps that
it was undoubtedly heliocentric as well as a major departure away from
the views perpetuated by organized religion.
Thus it may have come too late, a century after Linneaus'
classifications, a little less with respect to Cook's voyages, and half
a century or more
of continued activity that was simply too much for those who wished to
maintain the status quo. But what else took place during this
period of hopeful enlightenment only to fade from view? For that we turn next to the
perhaps unexpected subject of spiral formations in shells.
Before this, however, it seems fitting to leave the present section and the Three-fold Number with the starting paragraph from the Prologue to the Theory of the Planets (Theorica planetarium) by Campanus of Navara:31
The foremost master of philosophy divides the province of that [subject] into three primary genera; the first of these he names theological, the second mathematical, and the third natural. And the middle term becomes in a way a partaker in the nature of the two extreme terms, because mathematical principles are found in the realms of nature and theology alike, and because it ranks below the first and above the third in nobility of subject matter, although both of them yield place to it with respect to certainty of the method of teaching; this is the reason, moreover, why it is called, by a transfer of epithet, “the teaching genus,” on the grounds that it possesses a method of teaching which the student cannot contradict. For it begins with things which are grasped by the intellect, namely, things self-evident to all men, and from these it deduces, by an infallible process, the first demonstrables, then the middle ones, then the last, proceeding from first to last through the middle ones in their due order. (Campanus of Navara, ca.1250 CE )
The principle of information coding by the brain seems to be based on the golden mean. Since decades psychologists have claimed memory span to be the missing link between psychometric intelligence and cognition. By applying Bose-Einstein-statistics to learning experiments, Pascual-Leone obtained a fit between predicted and tested span. Multiplying span by mental speed (bits processed per unit time) and using the entropy formula for bosons, we obtain the same result. If we understand span as the quantum number n of a harmonic oscillator, we obtain this result from the EEG. The metric of brain waves can always be understood as a superposition of n harmonics times 2 F, where half of the fundamental is the golden mean F (= 1.618) as the point of resonance. Such wave packets scaled in powers of the golden mean have to be understood as numbers with directions, where bifurcations occur at the edge of chaos, i.e. 2 F = 3+ f 3. Similarities with El Naschie’s theory for high energy particle’s physics are also discussed.
REFERENCES
Copyright © 2002. John N. Harris, M.A.(CMNS). Last updated on February 8, 2004.
Return to spirasolaris.ca