
A-1 THE MERCURY Mt-BASED
EXPONENTIAL PLANETARY FRAMEWORK
Although the exponential function P(x) = Mt phix
(x
= -2 to 16, base Mt = 0.240842658 years )
generates successive mean sidereal and mean synodic
periods from IMO to out beyond Pluto, the
resulting exponential function is (naturally enough) based on the
well-known Phi-Series., i.e.,
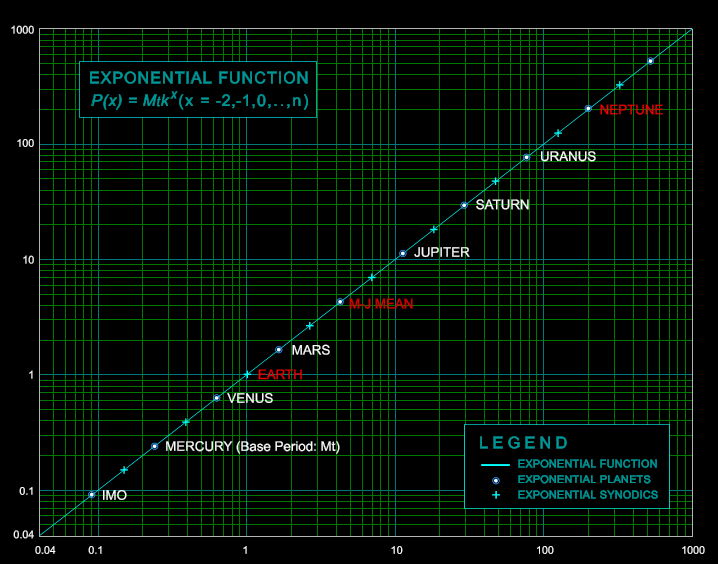
Table 1. The Phi-Series Exponential Planetary Framework
| N | PLANETS | PERIODS | DISTANCE | INVERSES | VELOCITY | Vi DIFFS | DIFFERENCES |
| -2 | IMO | 0.091505 | 0.2030631 | 0.4506252 | 2.2191392 | 2.2191392 | Next-Neptune |
| -1 | Synodic | 0.148059 | 0.2798698 | 0.5290272 | 1.8902620 | 1.8902620 | Syn 17-Syn 15 |
| 0 | MERCURY | 0.239564 | 0.3857279 | 0.6210700 | 1.6101245 | 1.6101245 | Neptune-Uranus |
| 1 | Synodic | 0.387623 | 0.5316260 | 0.7291269 | 1.3715035 | 1.3715035 | Syn 15-Syn 13 |
| 2 | VENUS | 0.627187 | 0.7327086 | 0.8559840 | 1.1682461 | 1.1682461 | Uranus-Saturn |
| 3 | Earth/Synodic | 1.014810 | 1.0098489 | 1.0049124 | 0.9951117 | 0.9951117 | Syn 13-Syn 11 |
| 4 | MARS | 1.641996 | 1.3918149 | 1.1797520 | 0.8476357 | 0.8476357 | Saturn-Jupiter |
| 5 | Synodic | 2.656806 | 1.9182560 | 1.3850112 | 0.7220158 | 0.7220158 | Syn 11-Syn 9 |
| 6 | AST.BELT | 4.298802 | 2.6438186 | 1.6259824 | 0.6150128 | 0.6150128 | Jupiter-Ast.Belt |
| 7 | Synodic | 6.955608 | 3.6438186 | 1.9088789 | 0.5238677 | 0.5238677 | Syn 9-Syn 7 |
| 8 | JUPITER | 11.25441 | 5.0220594 | 2.2409952 | 0.4462303 | 0.4462303 | Ast.Belt-Mars |
| 9 | Synodic | 18.21002 | 6.9216070 | 2.6308947 | 0.3800988 | 0.3800988 | Syn 7-Syn 5 |
| 10 | SATURN | 29.46443 | 9.5396410 | 3.0886309 | 0.3237680 | 0.3237680 | Mars-Venus |
| 11 | Synodic | 47.67445 | 13.147922 | 3.6260064 | 0.2757855 | 0.2757855 | Syn 5-Syn 3 |
| 12 | URANUS | 77.13888 | 18.121002 | 4.2568771 | 0.2349140 | 0.2349140 | Venus-Mercury |
| 13 | Synodic | 124.8133 | 24.975104 | 4.9975098 | 0.2000997 | 0.2000997 | Syn 3-Syn 1 |
| 14 | NEPTUNE | 201.9522 | 34.421707 | 5.8670016 | 0.1704448 | 0.1704448 | Mercury-IMO |
| 15 | Synodic | 326.7655 | 47.441400 | 6.8877718 | 0.1451848 | ||
| 16 | NEXT | 528.7177 | 65.385672 | 8.0861408 | 0.1236684 |
Table 2. The Mt3 Based Exponential Planetary Framework
B. THE
PHI-SERIES AND THE SOLAR SYSTEM
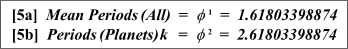
Relations 5a and 5b. The Fundamental Period Constants

Relations 6a and 6b. The Fundamental Distance Constants
Thus with relation 6b we obtain a constant increase in mean planetary distances of 1.88995476295... as opposed to the ad hoc multiples of 2 that belong to the Titius-Bode relationship. But even so, this still leaves an unaccounted "gap" between Mars and Jupiter. For more on this complex topic see Figure 6 and part F below.
C. THE
PHI-BASED EQUIANGULAR PERIOD SPIRAL
![]() Although the above digressions
and what follows next impinge on matters discussed in Part IV and later
sections, returning to the technical side of the matter there seems
little
doubt that the phi-based exponential planetary frameworks can (and
likely
should) be considered in terms of equiangular period spirals based on
relation
5b expressed in the form:
Although the above digressions
and what follows next impinge on matters discussed in Part IV and later
sections, returning to the technical side of the matter there seems
little
doubt that the phi-based exponential planetary frameworks can (and
likely
should) be considered in terms of equiangular period spirals based on
relation
5b expressed in the form:

Relation 9. The Exponential Period Function and Equiangular Period Spiral [ from Part IV ]
The resulting spiral (see Part IV) is
predicated on the
equiangular "square" dictated
by relation 5b, i.e., the Phi-squared increase in mean planetary
periods.
Thus for example, Figure 6c incorporates the Phi-Series mean sidereal
and
mean synodic periods from Mercury to Mars:
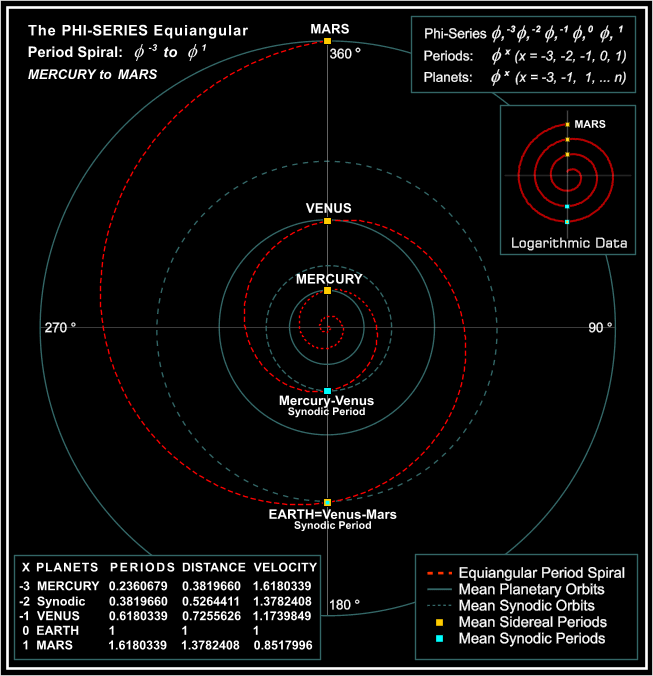
Figure 6c. The Phi-Series Equiangular Period Spiral from Mercury to Mars
![]() Delineated on the vertical
axis, the mean planetary periods increase by Phi squared per sidereal
revolution
of 360 degrees while the synodic periods occur at the 180-degree
half-cycle
points. Exactly the same configuration could be given for the
Phi-Series
periods for Jupiter, Saturn and Uranus (or indeed any such segment of
the
Phi-Series) since the periods increase in the same manner, whereas a
uniform
(i.e., log-linear) representation necessarily requires logarithmic data
in addition, as shown in the inset. But there is far more to this
equiangular
spiral, for although the above represents Solar System mean periods,
i.e.,
Time, it turns out that to produce corresponding equiangular
distance
and velocity spirals would be entirely redundant, for both sets of
parameters
are already integral features of period spiral itself. The details are
discussed further in Part IV, but small wonder that Jacob Bernoulli
should
have called the equiangular spiral "Spira Mirabilis" and included it on
his tombstone, or that part of the title is retained here, albeit
shared
with Archytas for reasons that will become apparent in the next few
sections.
Delineated on the vertical
axis, the mean planetary periods increase by Phi squared per sidereal
revolution
of 360 degrees while the synodic periods occur at the 180-degree
half-cycle
points. Exactly the same configuration could be given for the
Phi-Series
periods for Jupiter, Saturn and Uranus (or indeed any such segment of
the
Phi-Series) since the periods increase in the same manner, whereas a
uniform
(i.e., log-linear) representation necessarily requires logarithmic data
in addition, as shown in the inset. But there is far more to this
equiangular
spiral, for although the above represents Solar System mean periods,
i.e.,
Time, it turns out that to produce corresponding equiangular
distance
and velocity spirals would be entirely redundant, for both sets of
parameters
are already integral features of period spiral itself. The details are
discussed further in Part IV, but small wonder that Jacob Bernoulli
should
have called the equiangular spiral "Spira Mirabilis" and included it on
his tombstone, or that part of the title is retained here, albeit
shared
with Archytas for reasons that will become apparent in the next few
sections.
![]() On a more recent historical
note, investigation reveals that research concerning the spiral form in
related astronomical contexts includes the work of Lothar Komp in 1996
(see F1. below) and William M. Malisoff in 1929. For the latter's
inclusion
of velocities, distances, periods and the logarithmic spiral see
paragraph
(7) in his 1929 letter to the editor of the Science ("Some
New Laws of the Solar System".)
On a more recent historical
note, investigation reveals that research concerning the spiral form in
related astronomical contexts includes the work of Lothar Komp in 1996
(see F1. below) and William M. Malisoff in 1929. For the latter's
inclusion
of velocities, distances, periods and the logarithmic spiral see
paragraph
(7) in his 1929 letter to the editor of the Science ("Some
New Laws of the Solar System".)
D.
PHYLLOTAXIS AND THE EXPONENTIAL PLANETARY FRAMEWORKS
![]() Although the present treatment
has concentrated on Time, it now becomes necessary to consider
the
results in terms of the relationship between Phi, the Fibonacci Series
and natural growth. In other words, physical considerations concerning
growth itself, with time, "distance" and speed (i.e., rate of growth)
integral
components. So far the generated exponential planetary frameworks have
largerly concerned the mean periods, i.e., time, but as understood from
the outset, this was to obtain more data, new methodology and a more
productive
approach to the structure of the Solar System. Carried though all this,
however, were still the inter-relationships between Time, Distance and
Velocity provided by the velocity expansions to the third law of
planetary
motion and the third law itself. Moreover, as can be seen in Figure 6c,
the obvious complexities of the Phi Series in this specific
astronomical
context reveal that the exact values for the mean periods also
occur
elsewhere in the table among the mean Velocities (e.g., the
mean
sidereal period of Mars and the mean velocity of Mercury; see also
Table
1) in a complex, if not distinctly "ourobotic" context that will be
discussed
in later Sections. As for the occurrence of the Phi Series in the
present
context, those unfamilar with the subject might wish to bear in mind
that
Phi, the Fibonacci, Lucas and related series, far from being confined
to
plant and animal growth alone, occur in numerous diverse
contexts over an enormous range that extends from the structure of
quasi-crystals
out to the very structure of spiral galaxies. And this being so, should
there really be any great surprise if Phi should also prove to be an
underlying
element in the structure of planetary systems?
It has long been
recognized that although Phi and the Fibonacci Series are intimately
related
to the subject of natural growth that they are hardly limited to these
two fields alone. Remaining with the Phi-Series, Jay Kappraff 3
points out that the French architext Le Corbusier "developed
a linear scale of lengths based on the irrational number (phi), the
golden
mean, through the double geometric and Fibonacci (phi) series" for his
Modular
System. The latter's interest in the topic is explained further in the
following informative passage from Jay Kappraff's CONNECTIONS
: The Geometric Bridge between Art and Science:
Although the present treatment
has concentrated on Time, it now becomes necessary to consider
the
results in terms of the relationship between Phi, the Fibonacci Series
and natural growth. In other words, physical considerations concerning
growth itself, with time, "distance" and speed (i.e., rate of growth)
integral
components. So far the generated exponential planetary frameworks have
largerly concerned the mean periods, i.e., time, but as understood from
the outset, this was to obtain more data, new methodology and a more
productive
approach to the structure of the Solar System. Carried though all this,
however, were still the inter-relationships between Time, Distance and
Velocity provided by the velocity expansions to the third law of
planetary
motion and the third law itself. Moreover, as can be seen in Figure 6c,
the obvious complexities of the Phi Series in this specific
astronomical
context reveal that the exact values for the mean periods also
occur
elsewhere in the table among the mean Velocities (e.g., the
mean
sidereal period of Mars and the mean velocity of Mercury; see also
Table
1) in a complex, if not distinctly "ourobotic" context that will be
discussed
in later Sections. As for the occurrence of the Phi Series in the
present
context, those unfamilar with the subject might wish to bear in mind
that
Phi, the Fibonacci, Lucas and related series, far from being confined
to
plant and animal growth alone, occur in numerous diverse
contexts over an enormous range that extends from the structure of
quasi-crystals
out to the very structure of spiral galaxies. And this being so, should
there really be any great surprise if Phi should also prove to be an
underlying
element in the structure of planetary systems?
It has long been
recognized that although Phi and the Fibonacci Series are intimately
related
to the subject of natural growth that they are hardly limited to these
two fields alone. Remaining with the Phi-Series, Jay Kappraff 3
points out that the French architext Le Corbusier "developed
a linear scale of lengths based on the irrational number (phi), the
golden
mean, through the double geometric and Fibonacci (phi) series" for his
Modular
System. The latter's interest in the topic is explained further in the
following informative passage from Jay Kappraff's CONNECTIONS
: The Geometric Bridge between Art and Science:
As a young man, Le Coubusier studied the elaborate spiral patterns of stalks, or paristiches as they are called, on the surface of pine cones, sunflowers, pineapples, and other plants. This led him to make certain observations about plant growth that have been known to botanists for over a century.A great deal of additional information concerning this complex topic is obtainable from the above work and the other references, but for the present it is sufficient to return to the ongoing line of inquiry, noting from the various examples cited, that actual phyllotaxic ratios in nature do not necessarily produce Phi itself--the limiting value of Fibonacci and Lucas ratios--but numbers obtained from ratios much closer to the commencing sequence: 1,1,2,3,5,8,13,21,... For example, the ratios 8:5 = 1.6, 13:8 = 1.625 and somewhat closer to Phi, the ratio 89:55 that results in 1.6181818...
Plants, such as sunflowers, grow by laying down leaves or stalks on an approximately planar surface. The stalks are placed successively around the periphery of the surface. Other plants such as pineapples or pinecones lay down their stalks on the surface of a distorted cylinder. Each stalk is displaced from the preceding stalk by a constant angle as measured from the base of the plant, coupled with a radial motion either inward or outward from the center for the case of the sunflower [see Figure 3.21 (b)] or up a spiral ramp as on the surface of the pineapple. The angular displacement is called the divergence angle and is related to the golden mean. The radial or vertical motion is measured by the pitch h. The dynamics of plant growth can be described by and h; we will explore this further in Section 6.9 [Coxeter, 1953].
Each stalk lies on two nearly orthogonally intersecting logarithmic spirals, one clockwise and the other counterclockwise. The numbers of counterclockwise and clockwise spirals on the surface of the plants are generally successive numbers from the F series, but for some species of plants they are successive numbers from other Fibonacci series such as the Lucas series. These successive numbers are called the phyllotaxis numbers of the plant. For example, there are 55 clockwise and 89 counterclockwise spirals lying on the surface of the sunflower; thus sunflowers are said to have 55, 89 phyllotaxis. On the other hand, pineapples are examples of 5, 8 phyllotaxis (although, since 13 counterclockwise spirals are also evident on the surface of a pineapple, it is sometimes referred to as 5, 8, 13 phyllotaxis). We will analyze the surface structure of the pineapple in greater detail in Section 6.9.3.7.2 Nature responds to a physical constraint After more than 100 years of study, just what causes plants to grow in accord with the dictates of Fibonacci series and the golden mean remains a mystery. However, recent studies suggest some promising hypotheses as to why such patterns occur [Jean, 1984], [Marzec and Kappraff, 1983], [Erickson, 1983].
A model of plant growth developed by Alan Turing states that the elaborate patterns observed on the surface of plants are the consequence of a simple growth principle, namely, that new growth occurs in places "where there is the most room," and some kind of as-yet undiscovered growth hormone orchestrates this process. However, Roger Jean suggests that a phenomenological explanation based on diffusion is not necessary to explain phyllotaxis. Rather, the particular geometry observed in plants may be the result of minimizing an entropy functionsuch as he introduces in his paper [1990].
Actual measurements and theoretical considerations indicate that both Turing's diffusion model and Jean's entropy model are best satisfied when successive stalks are laid down at regular intervals of 2Pi /Phi^ 2 radians, or 137.5 degrees about a growth center, as Figure 3.22 illustrates for a celery plant. The centers of gravity of several stalks conform to this principle. One clockwise and one counterclockwise logarithmic spiral wind through the stalks giving an example of 1,1 phyllotaxis.
The points representing the centers of gravity are projected onto the circumference of a circle in Figure 3.23, and points corresponding to the sequence of successive iterations of the divergence angle, 2Pi n/Phi^ 2, are shown for values of n from 1 to 10 placed in 10 equal sectors of the circle. Notice how the corresponding stalks are placed so that only one stalk occurs in each sector. This is a consequence of the following spacing theorem that is used by computer scientists for efficient parsing schemes [Knuth, 1980].Theorem 3.3 Let x be any irrational number. When the points [x] f, [2x] f, [3x] f,..., [nx] f are placed on the line segment [0,1], the n + 1 resulting line segments have at most three different lengths.Here clock arithmetic based on the unit interval, or mod 1 as mathematicians refer to it, is used, as shown in Figure 3.24, in place of the interval mod 2pi around the plant stem. It turns out that segments of various lengths are created and destroyed in a first-in-first-out manner. Of course, some irrational numbers are better than others at spacing intervals evenly. For example, an irrational that is near 0 or I will start out with many small intervals and one large one. Marzec and Kappraff [1983] have shown that the two numbers 1/Phi and 1/Phi^2 lead to the "most uniformly distributed" sequence among all numbers between Phi and 1. These numbers section the largest interval into the golden mean ratio,Phi :l, much as the blue series breaks the intervals of the red series in the golden ratio.
Moreover, [(n + 1)x] f will fall into one of the largest existing segments. ( [ ] f means "fractional part of ").
Thus nature provides a system for proportioning the growth of plants that satisfies the three canons of architecture (see Section 1.1). All modules (stalks) are isotropic (identical) and they are related to the whole structure of the plant through self-similar spirals proportioned by the golden mean. As the plant responds to the unpredictable elements of wind, rain, etc., enough variation is built into the patterns to make the outward appearance aesthetically appealing (nonmonotonous). This may also explain why Le Corbusier was inspired by plant growth to recreate some of its aspects as part of the Modulor system.
(Jay Kappraff, Chapter 3.7. The Golden Mean and Patterns of Plant Growth, CONNECTIONS : The Geometric Bridge between Art and Science, McGraw-Hill, Inc. New York, 1991:89-96, bold emphases suppplied. See also Dr. Ron Knott's extensive treatment The Fibonacci Numbers and the Golden Section, the latter's related links and the The Phyllotaxis Home Page of Smith University)
![]() With respect to the Phi-series
and the exponential planetary frameworks under consideration, accepting
(a) that an exponential component does exist in the structure
of
the Solar System, and (b) that the inverse-velocity relationships are
indeed an integral feature of the latter, then it becomes possible to
consider
phyllotaxis in this explicit context, especially since the spiral form
can be considered to be operating here also. At which point it may be
recalled
that in seeking to reduce the common minor deviations in the
inverse-velocity
relationships in the Phi-based planetary frameworks a substitute base
period
for Mercury (Mt3 = 0.2395640) years was
applied
and Phi retained as the constant of linearity. However, although the
determinatiyon
of the new base period Mt3 was necessary in terms of the
initial framework, there was nevertheless another way that the common
deviations
could have been reduced to zero, namely the
substitution
of a slightly different value for the major constant Phi itself.
Or, if one wishes, the establishment of a practical ratio similar to
those
discussed above that nevertheless reduced all inverse-velocity errors
to
zero. This requirement is readily achieved by back-solving, resulting
in
the retention of the present day estimate for the mean sidereal period
of Mercury (Mt = 0.240827 years) as the base period but
the
substitution of a a new, slightly lower value of
1.6171413367027
for
the constant of linearity. With this substitution the minor deviations
in the inverse-velocity relationships are still reduced to zero while
the
resulting exponential planetary framework is found to differ only
marginally
from the other three (see Table 3 below).
With respect to the Phi-series
and the exponential planetary frameworks under consideration, accepting
(a) that an exponential component does exist in the structure
of
the Solar System, and (b) that the inverse-velocity relationships are
indeed an integral feature of the latter, then it becomes possible to
consider
phyllotaxis in this explicit context, especially since the spiral form
can be considered to be operating here also. At which point it may be
recalled
that in seeking to reduce the common minor deviations in the
inverse-velocity
relationships in the Phi-based planetary frameworks a substitute base
period
for Mercury (Mt3 = 0.2395640) years was
applied
and Phi retained as the constant of linearity. However, although the
determinatiyon
of the new base period Mt3 was necessary in terms of the
initial framework, there was nevertheless another way that the common
deviations
could have been reduced to zero, namely the
substitution
of a slightly different value for the major constant Phi itself.
Or, if one wishes, the establishment of a practical ratio similar to
those
discussed above that nevertheless reduced all inverse-velocity errors
to
zero. This requirement is readily achieved by back-solving, resulting
in
the retention of the present day estimate for the mean sidereal period
of Mercury (Mt = 0.240827 years) as the base period but
the
substitution of a a new, slightly lower value of
1.6171413367027
for
the constant of linearity. With this substitution the minor deviations
in the inverse-velocity relationships are still reduced to zero while
the
resulting exponential planetary framework is found to differ only
marginally
from the other three (see Table 3 below).
![]() The question that now arises
is of considerable interest, for how does this new constant of
linearity
compare with the Fibonacci and Lucas ratios discussed above in
association
with natural growth? Although not entirely comparable, it turns out
that
the zeroing constant is indeed close to some of the phyllotaxic ratios
in question, slightly lower, in fact, than the Sunflower's 89:55
phyllotaxis.
In other words, the value in question--1.617141336703--is
closest to the Lucas Series ratio 76
/ 47 followed by the Fibonacci
Series ratio of
55 / 34.
The occurrence of the Lucas ratio in this context is perhaps the least
surprising given the well-known relationship that exists between the
Phi
Series and the Lucas Series, namely that the difference between the two
is the value obtained from reciprocal exponent of the generating power
applied in the former. For example, in the Phi-Series exponential
planetary
framework the theoretical mean sidereal period of Uranus
(76.0131556174..
years) is generated by Phi raised to the ninth power, while Lucas
number
76 is less than this by exactly Phi to the minus ninth power,
i.e.,
0.0131556174.., and the same applies in the case of the eighth powers
and
the 47-year period, and so on. But is it pure coincidence that the
76 and 47-year periods correspond to the respective Phi
Series
periods for Uranus and the Saturn-Uranus synodic? And does the Lucas
Series
predominate here, or is there a Fibonacci component as suggested by
proximity
of the 55:34 ratio? Either way, there is little variance
between
the new exponential periods of the Lucas-Fibonacci (MtLF)
framework
and those provided by Mt3 and the two
previous
frameworks as shown in Table 3, which features the modern estimate for
the mean sidereal period of Mercury for the initial exponential
planetary
framework (Mt-based) and also the last variant that employs the
modified
constant of linearity. Noteworthy in the MtLF-based data (but possibly
coincidental) is the unforced correlation between the value for the
mean
sidereal period of Saturn of 29.45867 years in the latter and the
modern
estimate of 29.45252 years.
The question that now arises
is of considerable interest, for how does this new constant of
linearity
compare with the Fibonacci and Lucas ratios discussed above in
association
with natural growth? Although not entirely comparable, it turns out
that
the zeroing constant is indeed close to some of the phyllotaxic ratios
in question, slightly lower, in fact, than the Sunflower's 89:55
phyllotaxis.
In other words, the value in question--1.617141336703--is
closest to the Lucas Series ratio 76
/ 47 followed by the Fibonacci
Series ratio of
55 / 34.
The occurrence of the Lucas ratio in this context is perhaps the least
surprising given the well-known relationship that exists between the
Phi
Series and the Lucas Series, namely that the difference between the two
is the value obtained from reciprocal exponent of the generating power
applied in the former. For example, in the Phi-Series exponential
planetary
framework the theoretical mean sidereal period of Uranus
(76.0131556174..
years) is generated by Phi raised to the ninth power, while Lucas
number
76 is less than this by exactly Phi to the minus ninth power,
i.e.,
0.0131556174.., and the same applies in the case of the eighth powers
and
the 47-year period, and so on. But is it pure coincidence that the
76 and 47-year periods correspond to the respective Phi
Series
periods for Uranus and the Saturn-Uranus synodic? And does the Lucas
Series
predominate here, or is there a Fibonacci component as suggested by
proximity
of the 55:34 ratio? Either way, there is little variance
between
the new exponential periods of the Lucas-Fibonacci (MtLF)
framework
and those provided by Mt3 and the two
previous
frameworks as shown in Table 3, which features the modern estimate for
the mean sidereal period of Mercury for the initial exponential
planetary
framework (Mt-based) and also the last variant that employs the
modified
constant of linearity. Noteworthy in the MtLF-based data (but possibly
coincidental) is the unforced correlation between the value for the
mean
sidereal period of Saturn of 29.45867 years in the latter and the
modern
estimate of 29.45252 years.

Table 3. Comparison between Solar System Periods and the four exponential Frameworks.
![]() As explained above, the
MtLF exponential planetary framework also provides error-free
inverse-velocity
relationships, which perhaps suggests that it should provide the
preferred
planetary framework. The following log-linear representation of the
latter
as the diagonal reference line is applied to compress of the range of
the
periods and facilitate the comparison between the exponential
frameworks
and Solar system parameters. Here with the diagonal providing the
reference
frame, deviations above and below the line represent longer and shorter
periods respectively and thus also deviations in heliocentric distance,
i.e., the greater distance above the line the further out for from the
Sun, and below the line, the closer in with respect to the frame of
reference.
Thus the expected deviations for Pluto, Neptune, Mars and to a lesser
extent
Uranus are all evident, as is the suggested location of Earth in the
synodic
position between Venus and Mars. Also included in the comparison is the
Mars-Jupiter Mean and associated synodics on either side. One other
point
of interest is the suggestion of oscillatory "quenching" among the gas
giants (Neptune and Uranus especially) from the outer regions inwards
towards
the lower.
As explained above, the
MtLF exponential planetary framework also provides error-free
inverse-velocity
relationships, which perhaps suggests that it should provide the
preferred
planetary framework. The following log-linear representation of the
latter
as the diagonal reference line is applied to compress of the range of
the
periods and facilitate the comparison between the exponential
frameworks
and Solar system parameters. Here with the diagonal providing the
reference
frame, deviations above and below the line represent longer and shorter
periods respectively and thus also deviations in heliocentric distance,
i.e., the greater distance above the line the further out for from the
Sun, and below the line, the closer in with respect to the frame of
reference.
Thus the expected deviations for Pluto, Neptune, Mars and to a lesser
extent
Uranus are all evident, as is the suggested location of Earth in the
synodic
position between Venus and Mars. Also included in the comparison is the
Mars-Jupiter Mean and associated synodics on either side. One other
point
of interest is the suggestion of oscillatory "quenching" among the gas
giants (Neptune and Uranus especially) from the outer regions inwards
towards
the lower.

Figure 5. The MtLF Mean Periods and the Solar System: Mars-Jupiter Mean included
E. SIMILARITIES AND
DIFFERENCES
![]() A visual
comparison
between the twelve mean periods of the Mt3-based
planetary
framework and Solar System mean data is provided in Figure
5 (for data concerning Neptune and Pluto see Table 3).
The next and outermost theoretical planetary position (period:
526.8669
years; mean distance: 65.233 A.U.) provides the
inverse-velocity
data for IMO although there is no known planet in the
region.
However, it is relevant to note here that Clyde W. Tombaugh (the
discoverer
of Pluto) wrote in 1980 that the search for a tenth Solar System planet
occasioned a number of reports, mostly arising from observed
irregularities
in the orbits of known objects. Although it remained unconfirmed, a
planet
with a mean distance of 65.5 A.U. was in
fact
proposed by Joseph L. Brady of the Lawrence Livermore Laboratory,
University
of California in 1972.4 Since
that time further proposals concerning a possible planet in the outer
regions
have been made by Van Flandern and Harrington, (50 A.U.-100
AU.),5
Whitmire
and Matese (80 A.U.),6
Anderson (78-100 A.U.),7 and
Powell (60.8 A.U., later modified to 39.8 A.U.)8
To
date no tenth planet has been found, but most of these proposals
require
planets with highly inclined orbits, large eccentricities, and
relatively
long intervals between returns, all of which complicate confirmation,
especially
for small objects.
However, further delineation on a wider scale
may eventually be forthcoming from the gravity-based analyses of
Aleksandr
N. Timofeev, Vladimir A. Timofeev and Lubov G. Timofeeva;9
see
also Aleksandr Timofeev's: Two
fundamental laws of nature in the gravity field.
A visual
comparison
between the twelve mean periods of the Mt3-based
planetary
framework and Solar System mean data is provided in Figure
5 (for data concerning Neptune and Pluto see Table 3).
The next and outermost theoretical planetary position (period:
526.8669
years; mean distance: 65.233 A.U.) provides the
inverse-velocity
data for IMO although there is no known planet in the
region.
However, it is relevant to note here that Clyde W. Tombaugh (the
discoverer
of Pluto) wrote in 1980 that the search for a tenth Solar System planet
occasioned a number of reports, mostly arising from observed
irregularities
in the orbits of known objects. Although it remained unconfirmed, a
planet
with a mean distance of 65.5 A.U. was in
fact
proposed by Joseph L. Brady of the Lawrence Livermore Laboratory,
University
of California in 1972.4 Since
that time further proposals concerning a possible planet in the outer
regions
have been made by Van Flandern and Harrington, (50 A.U.-100
AU.),5
Whitmire
and Matese (80 A.U.),6
Anderson (78-100 A.U.),7 and
Powell (60.8 A.U., later modified to 39.8 A.U.)8
To
date no tenth planet has been found, but most of these proposals
require
planets with highly inclined orbits, large eccentricities, and
relatively
long intervals between returns, all of which complicate confirmation,
especially
for small objects.
However, further delineation on a wider scale
may eventually be forthcoming from the gravity-based analyses of
Aleksandr
N. Timofeev, Vladimir A. Timofeev and Lubov G. Timofeeva;9
see
also Aleksandr Timofeev's: Two
fundamental laws of nature in the gravity field.
In terms of departures from the norm perhaps the most
difficult anomaly
to accept is that Earth may currently be occupying a resonant synodic
location between Venus and Mars. The establishment of the
heliocentric concept notwithstanding, it would still appear
inordinately
difficult to perceive the position of Earth as anything other than an
immutable
and unquestioned constant. However, the relatively recently advent of
Chaos
Theory, its application in astronomical contexts and the investigations
carried out by Sussman,10
Wisdom,11 Kerr,12
Milani,13 Laskar,14,16, 17
and others have now changed matters irrevocably. The Solar System can
now
no longer be wound backwards or forwards indefinitely like some
well-oiled
and well understood mechanical device, as Ivars Petersen18
recounted in Newton's Clock: Chaos in the Solar system.
Nor
can the positions of any of its various members be considered
sacrosanct,
not even that of Earth.
![]() Whether Earth has always been
in the synodic location between Venus and Mars and in such complex
resonant
relationships is uncertain, but the zone of habitability is generally
defined
by the orbits of the latter pair of planets, and it is an open question
whether life would necessarily have developed at either extremity, or
if
it had, whether it would have necessarily flourished, given the
large-scale
periodic extinctions which appear to have taken place at Earth's more
advantageous
central synodic location. This even suggests that a fortuitous element
may have played a role in the continuance, if not the very development
of life here on Earth, and that while life may still abound in the
universe,
it may not be quite as common-place as previously supposed. Whether
this
has a direct bearing on the negative results obtained over the last
four
decades by the Search for Extra-Terrestrial Intelligence (SETI) is,
however,
another matter altogether. (For an up-to-date analysis of the search
and
an alternative, see Gerry Zeitlin's 1997-1999 essay: OPEN
SETI: Rethinking the SETI Paradigm and the Future of SETI ).
Whether Earth has always been
in the synodic location between Venus and Mars and in such complex
resonant
relationships is uncertain, but the zone of habitability is generally
defined
by the orbits of the latter pair of planets, and it is an open question
whether life would necessarily have developed at either extremity, or
if
it had, whether it would have necessarily flourished, given the
large-scale
periodic extinctions which appear to have taken place at Earth's more
advantageous
central synodic location. This even suggests that a fortuitous element
may have played a role in the continuance, if not the very development
of life here on Earth, and that while life may still abound in the
universe,
it may not be quite as common-place as previously supposed. Whether
this
has a direct bearing on the negative results obtained over the last
four
decades by the Search for Extra-Terrestrial Intelligence (SETI) is,
however,
another matter altogether. (For an up-to-date analysis of the search
and
an alternative, see Gerry Zeitlin's 1997-1999 essay: OPEN
SETI: Rethinking the SETI Paradigm and the Future of SETI ).
![]() For present
purposes it may be noted that deviations exist between the Solar System
and the exponential planetary frameworks, and that depending on the
degree
of confidence assigned to the latter, it may be feasible to quantify
these
anomalies in terms of planetary masses, mean distances, and the
conservation
of angular momentum, etc. This still leaves the anomalous position of
Neptune,
but it is possible to suggest a number of scenarios based on
mass-distance
changes that might include a further belt of asteroids and/or cometary
material at approximately 65 astronomical units from the sun
periodically
perturbed by an object or objects in a eccentric polar orbit, etc.
Apart
from the exponential framework itself, very little of this is actually
new, though scenarios based on total angular momentum might well remain
problematic owing to uncertainties concerning the complete inventory
and
total mass of the Solar System itself. On the other hand, new avenues
and new insights concerning the structure of the Solar System have
already
begun to surface; e.g., the Fibonacci-related paper by Aleksandr N
Timofeev
entitled: "Sprouts of New Gravitation Without Mathematical Chimeras of
XX Century."
For present
purposes it may be noted that deviations exist between the Solar System
and the exponential planetary frameworks, and that depending on the
degree
of confidence assigned to the latter, it may be feasible to quantify
these
anomalies in terms of planetary masses, mean distances, and the
conservation
of angular momentum, etc. This still leaves the anomalous position of
Neptune,
but it is possible to suggest a number of scenarios based on
mass-distance
changes that might include a further belt of asteroids and/or cometary
material at approximately 65 astronomical units from the sun
periodically
perturbed by an object or objects in a eccentric polar orbit, etc.
Apart
from the exponential framework itself, very little of this is actually
new, though scenarios based on total angular momentum might well remain
problematic owing to uncertainties concerning the complete inventory
and
total mass of the Solar System itself. On the other hand, new avenues
and new insights concerning the structure of the Solar System have
already
begun to surface; e.g., the Fibonacci-related paper by Aleksandr N
Timofeev
entitled: "Sprouts of New Gravitation Without Mathematical Chimeras of
XX Century."
RE-ASSESSMENT FOR THE
NEW MILLENNIUM
In
looking
back
over the three years that have elapsed since this third section of
Spira
Solaris was first uploaded in 1997 I have come to realize that I have
been
somewhat slow to react and even slower to change in spite of a number
of
positive inputs concerning the present subject that arrived one way or
another via the Internet. This was partly because of an increasing
interest
in the historical side of the matter but also my own inability to
absorb
and act on the various inputs received.
his concern was indeed justified, for only minor differences in the associated mean distances produced departures from the excellent value for Phi shown in relation [S1]. But be that as it may, on examination it turns out that the relationship is nevertheless directly applicable to the Phi-Series planetary framework, and moreover, it not only applies to the mean distances, but also the mean periods throughout. Actually, it does lead to Phi when the Phi-Series Mean Periods are applied, and also the corresponding value for the distances (1.378240772 ) when the distances are applied in turn. The reason for this becomes clear when one reduces the periods involved to their associated exponents although it is unnecessary to repeat the analysis here. The initial derivation by Mr. Shanahan was therefore in one way erroneous, but in another, it might well have resulted in an awareness of the Phi-Series planetary framework. But this was not the end of the matter anyway, for the latter had forged ahead and produced further exponential relationships, including the following involving the mean distances of Mercury, Mars, Jupiter and Neptune (the mean distances used were 0.387099, 1.523691, 5.204829, 30.068963 A.U. respectively.
The agreement here is again excellent based on modern values for the mean distances, but the reader will recall that Jupiter, Mars and Neptune all deviate from the exponential planetary framework, the latter especially. Thus one would hardly expect the exponential equivalent of this relationship to show any real correlation. But surprisingly, it does, in fact it produces perfect agreement using the the Phi-Series mean distances. But how can this be, with so much divergence between the mean distances of the latter framework and the modern estimates? In the case of Neptune, for example the Phi-Series equivalent is 34.0859 A.U. compared to the modern mean distance used above of 30.0689 A.U. and there is also a marked difference between the distances for Mars in addition. Then there is the difference for Jupiter with a mean distance of 5.203336 A.U. compared to the Phi-Series value of 4.97308025 A.U., and also Uranus at 19.191264 A.U. versus 17.9442719 A.U. A puzzle certainly, but also an opportunity, for the differences could be considered in terms of adjustments made with respect to the exponential planetary framework. Why should there be adjustments of this kind in the Solar System? The most likely cause, if not the most obvious, would be some change or other in planetary masses and/or positions. If so, there are certainly places in the Solar System that immediately come to mind where this might have taken place--not only the Asteriod Belt, but also perhaps, in the region occupied by slightly anomalous Uranus. Or should one say highly anomalous Uranus with its axis tilted almost ninety degrees off the "vertical"--a planet that is truly rolling along its orbit; or barreling around it, if one wishes. Just how Uranus came to be in this unusual situation has not been established, although there have been a number of theories proposed, as Eric Burgess explains below, adding a few more points of interest for good measure:15
The axis of Uranus is tilted so as to lie almost in the plane of its orbit ... one speculation is that there was a catastrophic collision with another planetary body early in the planet's history. . . What could have caused this axial tilt? One possibility is soon after the planet's formation it was hit by an Earth-sized body. An impacting speed of about 64,000 kph might be sufficient, according to some calculations, to push the planet on its side.. . A major mystery about Uranus is the low heat flux from the interior ... .all the small (Uranian) satellites have . . . . extremely dark surfaces. . . .What is this surface material? All the Uranian satellites are darker than the satellites of Saturn .. Also the colour of the surfaces is grey, whereas many other Solar System satellites have a tendency towards redness. (Eric Burgess, Uranus and Neptune, Columbia University Press, New York, 1988:51)An impacting speed of about 64,000 kph translates into some 17.778 k/sec--an orbital velocity that corresponds to a distance of 2.7992 A.U., which places it in the central region of the Asteriod Belt, another enigma and a complex one at that. Again there are various theories that might be considered with respect to the latter, including either the breakup of a planetary body in the region and/or the ejection of a sizable amount mass from it. So perhaps there are two areas that may have required adjustment--the first being a loss of mass within the Asteriod Belt itself, and the second involving a possible loss of mass from Uranus, with the event in the latter region perhaps responsible for it. In other words, the collision may not only have knocked Uranus on its side, it may also have been of such force that it chipped off perhaps sufficient mass to require adjustments into the bargain. Either way the loss of mass would necessarily influence the total angular momentum and compensation would be required to maintain the conservation of energy. And since orbital angular momentum is a function of velocity, mass and distance, the slack would have to be taken up by an outward movement of one more of the other planets or Uranus itself.
F.
LUCAS AND FIBONACCI RESONANCES IN THE SOLAR SYSTEM

Systems of Planets and Moons as "Barred Spirals."
Spiral Galaxies, Logarithmic Spirals and Ratios
A precise hyperbolic cosine distance formula, i.e.,
A Barred Spiral and the Moons of Neptune
A Barred Spiral and the Moons of Uranus
A Barred Spiral and the Moons Jupiter
A Barred Spiral and the Moons of Saturn
A Barred Spiral and the Outer Planets
A Barred Spiral and the Inner Planets
Synodic and Sidereal motion
Planetary and lunar resonances
Resonances that included rotation rates
Resonances among the Asteriods
Solar Activity and Planetary motion
F.2 MEAN MOTION
RESONANCES

Figure 6. Log-linear representation of the Asteriod Belt with Mars-Jupiter Synodic and MJM (Mean)
Further out among the anomalous planets Neptune and Pluto there are additional resonances, and with respect to the former it is also known that both Earth and Neptune are locked in similar resonant relationships. Denoting synodic periods by Ts, inner and outer mean sidereal periods by T1 and T2 and resonant relationships by: T1 : Ts : T2, both planets are in fact in 2:1:1 resonant relationships with adjacent bodies (Earth with Mars; Neptune with Uranus) while Neptune is also locked in a further 3:2:1 resonant relationship with Pluto. The latter's mean period produces poor results throughout as a base parameter for the exponential frameworks, but in comparison to its neighbors the gas giants, this small planet is already anomalous on a number of counts. Undoubtedly problems exist with the location of Pluto in the present context, but it is nevertheless still Neptune that represents the major discrepancy in the outer regions of the Solar System. Whether resonances among the four major superior planets will shed any light on the matter remains to be seen, but there is far more to this whole matter than mean motion resonances in any case, since real-time resonances in the Solar System must also be addressed. The question that now arises is how best to investigate these resonances on one hand and display them effectively on the other.
F.3. REAL-TIME
RESONANCES: THE INFERIOR PLANETS
![]() For this purpose the methodology
of Bretagnon and Simon21
adapted
to time-series analysis is particularly useful, especially the power
series
data and formulas for deriving heliocentric distances. The adaptation
(given
in Times Series
Analysis)
will be explained in more detail later but for present purposes it is
sufficient
to note that for any part of a planet's orbit at any point in time the
instantaneous value of the radius vector can be treated as the mean
value
of an equivalent mean distance orbit and consequently also provide
corresponding
periods and velocities for the same. In other words, each planetary
orbit
may be considered in terms of successive mean motion orbits extending
outwards
from the shortest distance at perihelion to the longest at aphelion. In
this way not only the varying distances, but also the velocities and
periods
may be treated as continuous functions over successive intervals.
Instantaneous
values of successive radius vectors may then be used to generate
corresponding
periods that serve to illustrate some of the better-known resonances
among
the inferior and superior planets. With respect to the former,
particularly
the adjacent planets Venus, Earth and Mars there seems little doubt
that
from a dynamic viewpoint Earth's location between Venus and Mars is
highly
complex. In addition to the resonances listed by Lothar Komp it may be
noted that although the Venus-Mars mean synodic period is 0.914224
years, in practice the elliptical nature of the orbits of the three
planets
cause the instantaneous sidereal and synodic velocities to vary widely
and also periodically coincide. But Earth is not only locked in a 2:1:1
resonance with Mars, but also in a 13:5:8 resonant relationship
with Venus, which is itself linked to Mars by a further 3:2:1
resonance.
Moreover, a plot of the true varying sidereal and synodic motion in the
form of time-series data reveals the existence of even more complex
resonant
relationships as seen in see Figure 7 below:
For this purpose the methodology
of Bretagnon and Simon21
adapted
to time-series analysis is particularly useful, especially the power
series
data and formulas for deriving heliocentric distances. The adaptation
(given
in Times Series
Analysis)
will be explained in more detail later but for present purposes it is
sufficient
to note that for any part of a planet's orbit at any point in time the
instantaneous value of the radius vector can be treated as the mean
value
of an equivalent mean distance orbit and consequently also provide
corresponding
periods and velocities for the same. In other words, each planetary
orbit
may be considered in terms of successive mean motion orbits extending
outwards
from the shortest distance at perihelion to the longest at aphelion. In
this way not only the varying distances, but also the velocities and
periods
may be treated as continuous functions over successive intervals.
Instantaneous
values of successive radius vectors may then be used to generate
corresponding
periods that serve to illustrate some of the better-known resonances
among
the inferior and superior planets. With respect to the former,
particularly
the adjacent planets Venus, Earth and Mars there seems little doubt
that
from a dynamic viewpoint Earth's location between Venus and Mars is
highly
complex. In addition to the resonances listed by Lothar Komp it may be
noted that although the Venus-Mars mean synodic period is 0.914224
years, in practice the elliptical nature of the orbits of the three
planets
cause the instantaneous sidereal and synodic velocities to vary widely
and also periodically coincide. But Earth is not only locked in a 2:1:1
resonance with Mars, but also in a 13:5:8 resonant relationship
with Venus, which is itself linked to Mars by a further 3:2:1
resonance.
Moreover, a plot of the true varying sidereal and synodic motion in the
form of time-series data reveals the existence of even more complex
resonant
relationships as seen in see Figure 7 below:
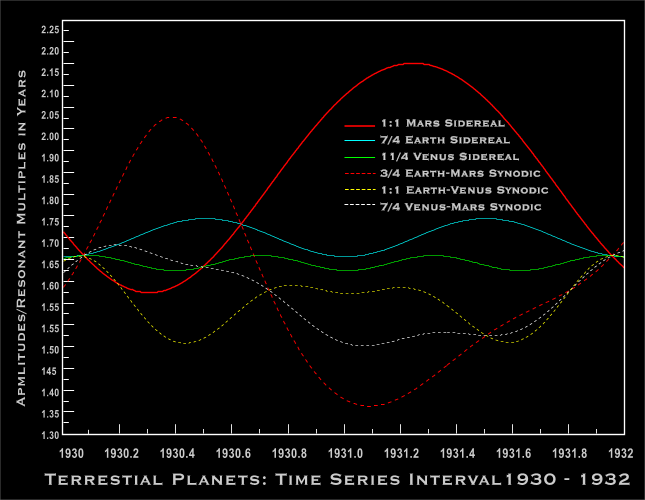
Figure 7. The Venus-Earth-Mars Resonances and the Lucas Series Numbers
This actual example
computed a number of years ago remains part of a
relatively inconclusive but not entirely negative investigation of
planetary
resonances and their possible inter-relationship with solar activity.
At
that time even the more obvious feature--that all the numbers involved
belong to the Lucas Series, i.e., 1,3,4,7,11 was not noted; nor
were the other resonances encountered examined in terms of the
Fibonacci
Series per se. The present example (which repeats after almost
thirty-two
years) is however but one of a number of approaches that can be applied
to the problem. It may be further noted here that in addition to
occupying
a resonant intermediate synodic location between Venus and Mars, that
the
corresponding inverse-velocity function for Earth may also defined in
terms
of the inverse-velocities of the three adjacent gas giants (the
Uranus-Saturn
and the Saturn-Jupiter synodics respectively) which are in turn subject
to real-time periodic variations of their own.
But there still remains the unexplained occurrence of the Lucas 76:47
and Fibonacci 55:34 ratios and why the former gives the better
correction
for the inverse-velocity functions in question. On the other hand,
there
is the apparent linkage between the major superior and the terrestrial
planets provided by the inverse-velocity functions and the undoubted
Fibonacci
relationships that exist among the more massive group of planets,
Jupiter
and Saturn especially.
F.4. REAL-TIME
RESONANCES: THE MAJOR SUPERIOR PLANETS
![]() Perhaps the best known resonance
in the Solar System involves the relative motion of Jupiter with
respect
to Saturn. But before examining this example in detail it is
necessarily
to emphasize the predominance of this pair of planets above all others,
including the adjacent major superior planets Uranus and Neptune. Alone
Jupiter accounts for 71% of the planetary mass in the Solar System and
more than half of the total angular momentum. Saturn comes next with
21%
of the mass and and 25% of the angular momentum; taken together Jupiter
and Saturn thus account for 92% of the mass and more than 85% of the
angular
momentum. The further inclusion of Uranus lifts the totals to 95% and
92%
respectively, while all four major superior planets account for more
than
99% of the planetary mass and more than 99% of the total angular
momentum
in the entire Solar System.
Perhaps the best known resonance
in the Solar System involves the relative motion of Jupiter with
respect
to Saturn. But before examining this example in detail it is
necessarily
to emphasize the predominance of this pair of planets above all others,
including the adjacent major superior planets Uranus and Neptune. Alone
Jupiter accounts for 71% of the planetary mass in the Solar System and
more than half of the total angular momentum. Saturn comes next with
21%
of the mass and and 25% of the angular momentum; taken together Jupiter
and Saturn thus account for 92% of the mass and more than 85% of the
angular
momentum. The further inclusion of Uranus lifts the totals to 95% and
92%
respectively, while all four major superior planets account for more
than
99% of the planetary mass and more than 99% of the total angular
momentum
in the entire Solar System.
![]() Of the four major planets,
the heliocentric positions of the first three not only compare to
successive
positions on the exponential planetary frameworks, they also permit the
generation of the three inverse-velocity relationships discussed in
Part
II. But there are other considerations to be factored into this complex
equation, for Jupiter is not only the largest planet by far in terms of
size and mass, it is also the swiftest moving major planet, followed in
due order by Saturn (the next most massive) and then Uranus. Neptune at
present represents an anomaly though it obviously cannot be ignored.
But
if one is going to concentrate on the major planets then it would be
logical
to expect that the influence of Jupiter and Saturn would predominate,
followed
next by Uranus. In other words, the three adjacent planets that belong
to the five successive sidereal and synodic periods from Jupiter out to
Uranus from the original log-linear segment. But since the sidereal and
synodic relationships between Jupiter, Saturn and Uranus have long been
known and to some extent researched, whatever it is that remains to be
determined must be more than this alone, or even perhaps entirely
different.
Then again, perhaps it is something relatively simple but difficult to
check exhaustively. Now at least the exponential planetary frameworks
provide
bases for comparison, as do the inverse-velocity relationships.
Finally,
the phyllotaxic Fibonacci/Lucas ratios at least permit the narrowing of
the inquiry to an investigation of real-time resonances among the the
four
most massive objects in the Solar System.
Of the four major planets,
the heliocentric positions of the first three not only compare to
successive
positions on the exponential planetary frameworks, they also permit the
generation of the three inverse-velocity relationships discussed in
Part
II. But there are other considerations to be factored into this complex
equation, for Jupiter is not only the largest planet by far in terms of
size and mass, it is also the swiftest moving major planet, followed in
due order by Saturn (the next most massive) and then Uranus. Neptune at
present represents an anomaly though it obviously cannot be ignored.
But
if one is going to concentrate on the major planets then it would be
logical
to expect that the influence of Jupiter and Saturn would predominate,
followed
next by Uranus. In other words, the three adjacent planets that belong
to the five successive sidereal and synodic periods from Jupiter out to
Uranus from the original log-linear segment. But since the sidereal and
synodic relationships between Jupiter, Saturn and Uranus have long been
known and to some extent researched, whatever it is that remains to be
determined must be more than this alone, or even perhaps entirely
different.
Then again, perhaps it is something relatively simple but difficult to
check exhaustively. Now at least the exponential planetary frameworks
provide
bases for comparison, as do the inverse-velocity relationships.
Finally,
the phyllotaxic Fibonacci/Lucas ratios at least permit the narrowing of
the inquiry to an investigation of real-time resonances among the the
four
most massive objects in the Solar System.
F.5. THE JUPITER-SATURN
CYCLES AND URANUS
![]() As mentioned earlier, the
present methods were first adapted a decade or more ago to generate
real-time
data to investigate the possible influence of planetary motion on Solar
Activity cycles--an investigation that included resonances, but not
exhaustively.
Here the same methods can be directed towards more specific goals,
though
it is as well to be aware of the complexities in attempting to come to
terms with interactions that involve multiple elliptical orbits and
varying
motion. A real-time period function for Jupiter will vary on either
side
of the mean sidereal period by the range permitted by the planet's
eccentricity,
in this case approximately 11 to 12.75 years and a similar situation
prevails
in the case of Saturn with a range of approximately 27 to 32 years. The
more complex Jupiter-Saturn synodic cycle on the other hand
has
a somewhat wider theoretical range (approximately 17 to 24 years) with
corresponding data derived from the synodic formula and periods
obtained
from the Jupiter-Saturn radius vectors. Time-series results in this
case
provide sinusoidal period functions that follow the variations of the
respective
radius vectors over time. Thus over approximately 59 years the 5:3:2
resonances of Jupiter and Saturn will be displayed as five sinusoidal
waveforms
for the former (i.e., 5 sidereal cycles), two sinusoidal cycles for
Saturn,
plus a three-cycle synodic waveform that maps the relative but varying
motion of Jupiter with respect to Saturn over the same interval.
"Resonances"
occur when all three waveforms coincide--three times in the present
example.
But before proceeding there are two further matters that require
explanation
and emphasis. The first is that as long as the basic 5:3:2 relationship
for Jupiter and Saturn holds, multiplications need not stop at the
approximate
59 year period; nor for that matter, need the well-known 1:1:2
resonance
of Uranus with respect to Neptune necessarily remain with unity (the
latter
provided by the mean period of Neptune), i.e.,
As mentioned earlier, the
present methods were first adapted a decade or more ago to generate
real-time
data to investigate the possible influence of planetary motion on Solar
Activity cycles--an investigation that included resonances, but not
exhaustively.
Here the same methods can be directed towards more specific goals,
though
it is as well to be aware of the complexities in attempting to come to
terms with interactions that involve multiple elliptical orbits and
varying
motion. A real-time period function for Jupiter will vary on either
side
of the mean sidereal period by the range permitted by the planet's
eccentricity,
in this case approximately 11 to 12.75 years and a similar situation
prevails
in the case of Saturn with a range of approximately 27 to 32 years. The
more complex Jupiter-Saturn synodic cycle on the other hand
has
a somewhat wider theoretical range (approximately 17 to 24 years) with
corresponding data derived from the synodic formula and periods
obtained
from the Jupiter-Saturn radius vectors. Time-series results in this
case
provide sinusoidal period functions that follow the variations of the
respective
radius vectors over time. Thus over approximately 59 years the 5:3:2
resonances of Jupiter and Saturn will be displayed as five sinusoidal
waveforms
for the former (i.e., 5 sidereal cycles), two sinusoidal cycles for
Saturn,
plus a three-cycle synodic waveform that maps the relative but varying
motion of Jupiter with respect to Saturn over the same interval.
"Resonances"
occur when all three waveforms coincide--three times in the present
example.
But before proceeding there are two further matters that require
explanation
and emphasis. The first is that as long as the basic 5:3:2 relationship
for Jupiter and Saturn holds, multiplications need not stop at the
approximate
59 year period; nor for that matter, need the well-known 1:1:2
resonance
of Uranus with respect to Neptune necessarily remain with unity (the
latter
provided by the mean period of Neptune), i.e.,

Figure 8. Jupiter-Saturn and Uranus-Neptune Resonances and the Fibonacci Series, 1940-1990.

Figure 8b. Multiple Jupiter-Saturn and Uranus-Neptune Resonances, 1890-1990.
At this juncture the matter begins to focus more firmly on the Fibonacci and Lucas Series, for in seeking to embrace the latter it seems that while it is still necessary to concentrate on the relative motion of Jupiter with respect to Saturn, the relative motion of Jupiter with respect to Uranus also has a significant role to play. The mean value of this period is readily obtained from the the mean sidereal periods of Jupiter and Uranus by way of the general synodic formula. Given to the sixth decimal the mean synodic period of Jupiter with respect to Uranus thus turns out to be 13.820371 years. What follows next is perhaps surprising, for in dealing with multiple harmonics--which is essentially what is under consideration here--it is one thing to invoke Fibonacci variants of the basic 5:3:2 resonant relationship between Jupiter and Saturn, and quite another to expect that the Jupiter-Uranus harmonics would relate to the Lucas Series in this precise context, especially in an opposite sense. Nor for that matter is it likely that one would anticipate that while it is necessary to reverse the order of the fibonacci triples to maintain the resonant relationship between Jupiter and Saturn (i.e., 5:3:2 to obtain 5 cycles of Jupiter, 3 Synodics and 2 cycles of Saturn in approximately 59 years, and so on), that the Lucas harmonic expansion would follow its normal order, i.e., 4, 7, 11, 18, 29, ... etc. But this being said, we are at least familiar with the Phi-Series planetary frameworks, the relationship between the latter and the Lucas Series and we are already dealing with the mean periods of revolution and synodic cycles expressed in years in both contexts. Again, however, bearing in mind the variance that results from the true orbital motions of the three planets in question, the relationship between the reversed Fibonacci triples and the Lucas harmonics is still not immediately apparent. One of the main reasons for this is that it only becomes clear after the multiple periods of the Jupiter-Saturn triples are averaged, and then only with the longer intervals is the relationship easily detectable. For example, based on a mean sidereal period of 11.869237 years for Jupiter, a corresponding mean synodic period 19.881324 years and mean sidereal period for Saturn of 29.452520 years, the fifth, third and second multiples (i.e., the 5:3:2 resonance) occur after 59.346 years, 59.644 years and 58.905 years respectively, whereas the average for all three products is 59.298 years. The fourth (4) Lucas augmentation of the Jupiter-Uranus mean synodic period on the other hand occurs after 55.282 years--a loose correlation easily dismissed as a chance occurrence. However, further investigation reveals that the 5:3:2 Jupiter-Saturn and Jupiter-Uranus Lucas multiple 4 are seemingly co-associated, for the next Lucas number (7) is similarly associated with the next reversed Fibonacci triple after 5:3:2, and as the two sets both proceed to their larger numbers, the difference between the averages of the Fibonacci triples and the Lucas multipliers becomes increasingly less. Thus by the time the 89:55:34 Fibonacci triple is reached the average of 1050.41 years is more closely approximated by the 1050.38 years obtained from the 76th multiple of the mean Jupiter-Uranus synodic cycle. In other words, the Fibonacci and Lucas assignments proceed sequentially, side-by-side in strict order. Thus the harmonic Fibonacci triples of the Jupiter-Saturn triad are related to the Lucas harmonics of the Jupiter-Uranus synodic cycle in the following manner for the given periods (rounded here to the nearest year for clarity and convenience):
5
3 -Lucas 4 ( 59 Years )
28
5 -Lucas 7 ( 94 Years )
313
8 -Lucas 11 ( 153 Years )
521
13 -Lucas 18 ( 248 Years )
834
21 -Lucas 29 ( 401 Years )
1355
34 -Lucas 47 ( 649 Years )
2189
55 -Lucas 76 ( 1050 Years )
34
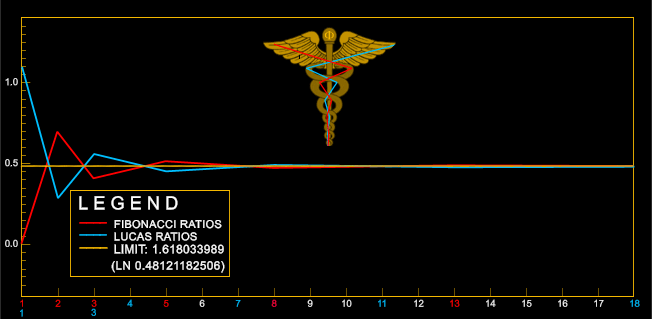
Figure 9. The
convergence towards the limit Phi by the Fibonacci
and Lucas Series Ratios.
Or is there more to
this matter in any case, including wider horizons with additional
degrees of complexity?
Consider, for example, the detailed arguments presented in the
following:

Table 4. The Jupiter-Saturn, Jupiter-Uranus Resonances and the Fibonacci/Lucas Series
Returning to the matter at hand, however, we have now arrive at the 76:47 Lucas ratio in true consort with the 55:34 Fibonacci ratio, with Lucas harmonics always occupying the position between the highest and next highest values in the associated Fibonacci triple. And here, as can be seen in Figure 10 -- real-time 89:55:34 multiples of the Jupiter-Saturn cycles and the 76th Jupiter-Uranus cycle -- the latter component also moves towards the nexus of the Jupiter-Saturn cycles, and this increasingly so with time. At which point it seems both relevant and useful to redirect the reader to Kurt Papke's Animation of Binet's Formula available on the Internet since 1998--a presentation that (speaking for myself, at least) only now comes into clearer focus.

Figure 10. The 89:55:34 Jupiter-Saturn and 76 Jupiter-Uranus Cycles, 1940-2000.
As a first approximation it therefore seems that the relative motions of Jupiter, Saturn and Uranus, and predominantly that of the first--the largest, swiftest and most massive of the three are intimately associated with the Golden Ratio. Not included here, yet likely also involved are the relative motions of Saturn with respect to Uranus, the motion of Saturn with respect to Neptune, and additional complications arising out the dominance provided by Jupiter with respect to all three. Nevertheless, the situation may be summarised at this initial stage in terms of the relative motions of the three major superior planets Jupiter, Saturn and Uranus as follows:

Figure 11. The Fundamental Fibonacci and Lucas Resonances; Jupiter-Saturn, Jupiter-Uranus
Where does this leave us? Is
it that surprising that the relative motion of Jupiter--firstly with
respect
to Saturn, and secondly with respect to Uranus--should predominate in
the
Solar System? And also, that the Golden Ratio should underly so much
order
and proportion in addition? Where does it all originate? That question
no doubt belongs to philosophical debates concerning the first of
things,
but if it is the product of the rel![]() ative motions of Jupiter, Saturn
and
Uranus, then it is little wonder that such ordering occurs if it is
indeed
resonating throughout the Solar System.
ative motions of Jupiter, Saturn
and
Uranus, then it is little wonder that such ordering occurs if it is
indeed
resonating throughout the Solar System.
![]() The above somewhat limited
discussion necessarily concerns complex waveforms and motions for the
mean, varying
and extremal values dictated by elliptical orbits.
The above somewhat limited
discussion necessarily concerns complex waveforms and motions for the
mean, varying
and extremal values dictated by elliptical orbits.
Although one could suggest that both the Fibonacci and the Lucas Series
are embedded in the Solar System, it might be more accurate to say that
they are in fact pulsating through it, and perhaps have been since time
immemorial.
GOLDEN
DIGRESSIONS
1. Babylonian.
2. Egyptian
REFERENCES
Copyright © 1997. John N. Harris, M.A.(CMNS). Last Updated on March 2, 2004.