BABYLONIAN PLANETARY THEORY AND THE HELIOCENTRIC CONCEPT
John N. Harris

I. PERIOD RELATIONS, PARAMETERS, AND PLANETARY THEORIES

Although the numerical methods and parameters found in the Babylonian Astronomical Procedure texts and Ephemerides of the Seleucid Era [310 B.C. - 75 A.D.] have been described in some detail, notably by Neugebauer (1955),1 (1975), 2 Van der Waerden (1974) 3 and others, it is far from certain whether the extant material represents the state of Babylonian astronomy per se, or merely scattered remnants of a larger corpus of knowledge. Moreover, what has been reclaimed can hardly be considered sequential or self-explanatory, while base-60 notation, unusual terminology, little-known phenomena and proclamations concerning the lack of a fictive model for Babylonian astronomy all prevent easy assimilation of the details. Then again, the information that has come down to us is itself scattered and fragmentary, ranging from earlier "Omens" through the detailed astronomical cuneiform texts of the Seleucid Era. In the latter context results exist in the form of "ephemerides" and at least part of the methodology is described (albeit in condensed form) in a number of related "procedure" texts, though none are particularly simple in the first place nor necessarily complete in the second. The recovery of the Babylonian astronomical cuneiform texts is also relatively recent (late 19th century onwards) as is the current understanding of their contents--an understanding unfortunately complicated by the necessary inclusion of Babylonian methodology within long-established time frames and the perceived flow of Greek astronomical thought. But while admiring Babylonian methodology most commentators nevertheless appear unwilling to grant that the Babylonians really understood what they were doing, or that they ever proceeded to determine a fictive planetary model. It is true (as far as is known) that the Babylonians did not use trignometrical methods in their astronomy, but then again neither did they confine their treatment of the planets to mean circular motion, or use auxiliary devices to reinforce unsupportable geocentric premises either. But there may be more sides to this issue in any event. We can hardly claim to know what exact prerogatives produced the known remnants of Babylonian astronomy from the Seleucid Era, and as evidenced by the known mathematical cuneiform texts of the Old Babylonian Period [1900-1650 BCE] Babylonian mathematics had already reached a remarkably high level some 1500 years earlier. It is unfortunate that there are no astronomical texts from the earlier period comparable to those of the Seleucid Era, but nevertheless there is little doubt that a sufficiently high level of mathematics was already in place during the former interval. Thus there are also considerable gaps during which time who knows what manner of investigations were carried out and what conclusions were reached, held, discarded and also perhaps passed down.
    Unfortunately, short of the recovery of further texts it is likely that we will never know, but nevertheless we can at least examine Babylonian astronomy in terms of its own distinctive successes in accounting for regular variations in both luni-solar and planetary motion.
Fig.1. The Seleucid Era and later planetary theories

Fig. 1. The Seleucid Era and later planetary theories
With the above in mind one of the main purposes of the present paper is to simplify matters wherever possible, and like it or not, the simplest way to achieve this end is to treat Babylonian methodology from a fictive heliocentric viewpoint. And indeed why not? This is surely a perfectly reasonable premise for the later period. After all, it includes the time of Aristarchus of Samos, and moreover, it is also generally accepted that single (not to mention incomplete) modified period relations of Babylonian origin are known to have provided the underlying bases for the later and diverse planetary planetary models proposed by Ptolemy, Al-Bitruji and Copernicus. But while the latter all employed uniform circular motion and auxiliary devices of one sort or another to account for variations in planetary velocity, the Babylonians for their part appear to have determined fundamental period relationships that were subsequently applied in numerical schemes concerned with both mean and varying orbital motion. This said, it is not the intention here to give a detailed comparative analysis of the later applications, but rather point out that there are distinct and critical differences between the latter and the more extensive corpus of Babylonian planetary period relations.

There no doubt even now remain champions of the status quo who will dutifully insist that Babylonian methodology represents mere counting and that their approach to planetary motion was entirely non-fictive. However, it is safe to suggest that none could explain how the Babylonians were able to differentiate the sidereal, anomalistic and draconic months from the synodic month by simple counting. Why stress luni-solar parameters when discussing Babylonian planetary theory and the heliocentric concept? Simply stated, the two are inextricably linked--not merely because of the fundamental units of time applied in Babylonian astronomy (days, tithi, mean synodic months and years) but also the inescapable fact that only the synodic month is directly observable. All the rest must be deduced, and this could hardly had been accomplished without applied conceptual reasoning and understanding--an understanding that would reasonably include planetary motion, though it need not have developed in precisely this way. In one sense the very simplicity of Babylonian methodology is itself misleading; but their concern with characteristic synodic phenomena leads naturally enough to an awareness of varying planetary motion, along with an understanding of the apparent retrogradations, stationary points and dates of appearance and disappearance, etc. And after gathering extensive sets of planetary period relations and generating various schemes to account for successive synodic phenomena and variations in velocity, it seems highly unlikely that the Babylonians managed to do so without developing a fictive model of any kind.

BABYLONIAN PERIOD RELATIONS
Apart from the terminology and notation, the extant planetary material of the Seleucid Era supplies reasonably straightforward procedures that are both instructive and informative. For example, for the three superior planets the Babylonians appear to have determined final planetary period relationships based on pairs of integer periods (called here T1 and T2) close to the mean sidereal period (or multiples thereof) with corresponding numbers of synodic periods and small, convenient corrections for longitude of opposite sign. In the case of Jupiter, Babylonian period relationships of 12 Years, 71 years, 83 Years, 95 years, 166 years and 261 years result in a final integer period relation of 427 years to which correspond 391 mean synodic arcs and 36 sidereal revolutions.4 The inter-relationship between the initial pair and the final 427-year period for Jupiter is shown in Table 1, the essence of a letter to the Editor of ISIS 5 published 26 years ago in 1977 in an unsuccessful bid to not only "close the circle" with respect to Babylonian orbits, but also to raise the issue of the heliocentric nature of Babylonian astronomy itself -- all to no avail.

Table.1 Babylonian Period Relations and the 427-year Period for Jupiter

Table.1 Babylonian Period Relations and the 427-year Period for Jupiter
Here the Babylonian 12-year and 71-year period relations are clearly intermediate in nature with positive and negative corrections for longitude that permit the generation of all the rest en route to the disarmingly simple 427-year final period (for the Babylonian application and use of this result see below). In this context the Babylonian period relations for 12 and 71 years (T1 and T2 respectively) represent an initial set, with neither one capable of generating particularly accurate results. Here the 71-year period corresponds to slightly less than 6 mean sidereal periods and 65 mean synodic arcs, i.e., six sidereal revolutions less a small correction; for the latter the Babylonians used two sets for both the fast and slow segments of the orbit, i.e.,
71 years corresponds to 6 x 360 - 5;00 degrees, 65 mean synodic periods/mean synodic arcs
71 years corresponds to 6 x 360 - 4;50 degrees, 65 mean synodic periods/mean synodic arcs
The historical significance of the above is seen in its similarity to the single period relationship for Jupiter utilized in Ptolemy's geocentric planetary model, i.e.,
71 Years - 4;54 days = 6 x 360 - 4;50 degrees = 65 Cycles (Anomaly)7
Applied to the heliocentric concept a similar variant was used in turn by Nicholas Copernicus, i.e.,
(71 Years - 5;54,13 days = 6 x 360 - 5;42,32 degrees = 65 Rotations in parallax8 )
while a further close variant was also applied by Al-Bitruji.

As for Babylonian methodology, without going into greater detail, in addition to the two initial periods and the final period relationship for Jupiter (Table 1 above), for Mars the three Babylonian periods with attendant small corrections for longitude of opposite sign (six sets) were T1 = 47 years, T2 = 79 years leading to the final (and remarkably accurate) integer period relationship of 284 years, 133 mean synodic periods and 151 mean sidereal periods, i.e., 151 sidereal revolutions.

For Saturn the corresponding three periods were in turn:
 T1 = 29 years, T2 = 59 years and final integer period relationship of 265 Years,
to which corresponded 256 mean synodic periods and 9 sidereal revolutions.
Nevertheless, instead of the 284-year and 265-year final periods for Mars and Saturn, all three later planetary theories were confined to their modified variants for the 79-year T2 and 59-year T2 periods alone, while further Babylonian periods appear to have been applied for the two inferior planets. Thus, despite their limitations there presently exist three quite different fictive planetary models (two geocentric and one heliocentric) each one based on similar, fractional and quite possibly misunderstood period relations of unquestioned Babylonian origin. At first acquaintance one might think that the 71-year period relation used by Ptolemy represents a refined and superior approach, but detailed examination reveals that this is simply not the case. In fact, instead of contriving to fit an inflexible geocentric framework and uniform circular motion to varying orbital motion and sequential synodic phenomena, the Babylonians delineated the latter with remarkable clarity and simplicity. Simple, yes, but hardly mindless or non-fictive. The planets do indeed move with varying velocity and the various synodic motions (i.e., relative motion as observed from Earth) do indeed exhibit apparent stationary points, apparent retrograde motions, along with first and last appearances in the east and the west as Earth moves around the Sun. The operative word here, of course, is "apparent" since to "save the phenomena" the successful accounting of the apparent motions of the planets is of paramount importance.

Thus the method applied by Ptolemy wins hands down?  Not in the least. Not one of Ptolemy's impressive looking planetary period relations actually produce the claimed motions in either longitude or anomaly, as Robert R. Newton pointed out in 1977 in The Crime of Claudius Ptolemy and other related works. Given to the sixth sexagesimal place and long touted as the epitome of accuracy, Ptolemy's daily planetary velocities are found to diverge from the stated values at or beyond the fourth sexagesimal place. Small errors? Perhaps, but hardly insignificant. Remember, if the phenomena cannot be saved by the data, then Ptolemy's geocentric model cannot be upheld either, never mind its fundamentally incorrect nature, its contrived use of uniform circular motion and additional, cumbersome auxiliary devices.  It has in fact always been defective and chronically so, in both detail and concept. Nor is it a question of the precise value of the year used by Ptolemy in his period relations either. Simply stated, there is no one single value for the year that will simultaneously correct the deviations in the Ptolemy's mean daily velocities.

Why the difference between the Babylonian and later applications? A complex question, no doubt, but one can suggest a number of factors that may have played their various roles, not least of all the intrusion of religious dogma on the scientific process and the fact that the later applications were all inherited, partial data, whereas the Babylonians were themselves the originators and collators of the original material. Frankly, one might have hoped that Newton's detailed analysis (one of the few original works on the subject since Al-Bitruji's earlier criticisms) might have helped generate fresh interest in Babylonian methodology, but unfortunately the subject still remains largely overshadowed by the Ptolemaic system, despite the latter's clear inaccuracies, fundamentally incorrect premises and dubious heritage. As for the earlier Babylonian approach, even a brief acquaintance with the parameters and the methodology should serve to raise a number of questions, not least of all how the notion that Babylonian astronomy lacked of a fictive planetary theory ever arose, let alone how it came to take root, and apparently still flourishes.

II. LUNI-SOLAR PARAMETERS AND PRECESSION
One of the fundamental units of time and motion applied in Babylonian astronomy appears to have been the mean synodic month of 29;31,50,8,20 days.13 This accurate Babylonian constant (29.53059413 days; the modern estimate is 29.53059027 days) is applied to mean and varying orbital velocities in both planetary and luni-solar contexts. The latter includes further attested Babylonian months, e.g., the mean sidereal month of 27;19,18 days (27.3216667),14 the anomalistic month of 27;33,16,20 days (27.5545370)15 and the draconic month of 27;12,43,56 days (27.21220370)16 in complex numerical contexts concerned largely with the 223-month Saros eclipse cycle. But the real significance of the inclusion of both the synodic and sidereal months in this context lies firstly in their difference, which for the mean values provides the mean motion of Earth and an implicit Babylonian sidereal year of 365.25646981 days (the modern  sidereal year is 365.25635674 days) Although the implicit value for the sidereal year mentioned above is not attested in the Babylonian material, a year of 365;14,44,51 days (365.24579166) is nevertheless mentioned in a lunar procedure text.17 The calendaric year on the other hand was obtained from a 19-year, 235 mean synodic month relationship (365.24682220 days) while the conveniently rounded year of 12;22,8 mean synodic months (365.26063766 days) appears to have been more generally employed in astronomical contexts. However, apart from Hartner's obliquely asserted Babylonian estimate for annual precession of approximately 45 seconds of arc,18 it is not generally acknowledged that the Babylonians differentiated between the tropical and sidereal years at all. Nevertheless, the latter Babylonian pair may represent convenient approximations that are greater than their modern equivalents by merely 0.43% and 0.46% respectively. As a consequence, they implicitly maintain the correct relationship between the two types of years with a difference between the sidereal and tropical year that yields an excellent value for annual precession of slightly more than 49 seconds of arc. And indeed why not; with the heliocentric concept deduced and firmly in place all manner of details could be investigated and over time, quite likely, amply refined.

Either way, like much of the extant material, the various lengths of the "year" in Babylonian astronomy deserve far more than casual consideration and unsupported rejection. The rounded Babylonian estimate for year of 12;22,8 mean synodic months is almost certainly one of convenience but it nevertheless has subtle underpinnings with 360 degrees of motion (solar or terrestrial) corresponding to a mean monthly progress of 29;06,19,00,55,37,24,... degrees. This may be compared to the mean monthly arc of 29;6,19,20 degrees19utilized in a Babylonian System B variable velocity function for the moon that increases and decreases between minimum and maximum monthly arcs of m = 28;10,39,40 degrees and M = 30;1,59,20 degrees respectively. The division of 360 degrees by the mean value for the Babylonian synodic month (29;06,19,20) results in a year of 12;22,7,51,54,7,4,..months (365.2595295509 days) with a corresponding mean daily velocity of 0;59,8,9,43,22,7,. degrees. Abbreviated at the fifth sexagesimal place (from "22" to "20"), the latter produces a corresponding year of 365.2595305603 days (the modern anomalistic year is 365.259641204 days). This daily parameter may also have been employed in a daily System B velocity function determined by Aaboe 20 from a fragmentary set of undated solar longitudes which apparently increased and decreased by 0;00,01,43,42,13,20 (0.0004801097) degrees per day. Although unattested, the resulting extrema for a mean daily velocity (u) of 0;59,8,9,43,20 degrees per day would have a maximum velocity (M) of 1;01,45,59,24,50 degrees per day and minimum daily velocity (m) of 0;56,30,20,01,50 degrees.

III. THE CLIMATE OF THE TIME
Just why the notion that Babylonian astronomers possessed no fictive planetary model of their own persists is unclear, especially since the variable velocity functions used to account for the motions of the Sun (or Earth), Moon and the three known superior planets suggest that the Babylonians were at least half right in their fundamental approach to planetary motion. Moreover, the various Babylonian schemes employed to concurrently describe the uninterrupted synodic arc in terms of forward motion, stationary points and retrogradations prove on further examination to be more than sufficient to "save the phenomena." Nor should this be any real surprise given the "definite opinion" of Seleucus (ca. 150 B.C.) on this matter recorded by Plutarch (On the Face in the Moon's Orb):
Did Plato put the Earth in motion as he did the sun, the moon and the five planets which he called 'the instruments of time' on account of their turnings, and was it necessary to conceive that the Earth ... was not represented as being (merely) held together and at rest but as turning and revolving, as Aristarchus and Seleucus afterwards maintained that it did, the former of whom stated this as only a hypothesis, the latter as a definite opinion?
The attested subdivision of integer multiples of 360 degrees of uninterrupted sidereal motion by the number of synodic occurrences in the final Babylonian period relationships result in the determination of the mean synodic arcs. But such subdivisions can hardly take place without respect to a center if they are to have any meaning whatsoever. As a consequence, it is natural and necessary to ask whether a common center can be found in Babylonian astronomy, and if so, where the common center might lie. Furthermore, if a possibly out-of-context fraction of the Babylonian material sufficed to provide the frameworks for the later planetary theories of Ptolemy, Al-Bitruji, and Copernicus, then what would have prevented the Babylonians - the originators, observers, and collators of extended sets of periods and related data - from developing a fictive planetary model of their own? Babylonian methodology clearly involved both sidereal and synodic motion, and although the latter was subdivided into "characteristic phenomena" rarely applied in modern astronomy the concept is nevertheless useful and logical in both its execution and its outcome. Moreover, even the simplest Babylonian treatment of varying synodic velocity involved the division of 360 degrees of sidereal motion into "Fast" and "Slow" arcs (System A) while Babylonian varying velocity functions (System B) are obviously quite sophisticated, especially in the case of Jupiter, with the line of apsides and also the position of mean velocity located on the ecliptic with an accuracy of one degree. The corresponding maximum, mean, and minimum synodic velocities for Jupiter were determined to be 38;02 degrees, 33;08,45 degrees and 28;15,30 degrees respectively with a rate of change of velocity that was understood to increase (or decrease, depending on location) by 1;48 degrees per synodic cycle. Although the available information for Saturn and Mars is less extensive, it is now known that the Babylonians determined System B functions for both. Given the relatively high eccentricity, swift motion and proximity to Earth, this was no mean achievement in the case of Mars. Although conjectural, it also appears possible that System B was similarly determined for Mercury (deduced from ACT 816, pp. 425-428; for further details see the Methodology below).

IV. BABYLONIAN PERIOD RELATIONS
As noted earlier, the Babylonian fundamental period relationships for the three superior planets appear to have depended on the selection of two integer periods (T1 and T2) close to mean periods of revolution (or multiples thereof) for which small, convenient corrections for longitude of opposite sign were determined. The frame of reference for these corrections was provided by some 33 "normal" or "Goal-Year" Stars distributed along and around the ecliptic. The details are found in the "Goal-Year" Texts 21 while intriguing atypical examples that include latitude provide further insights.22 Key relations for Jupiter are given in Section 1 of ACT 813 (translator: A. Sachs): 23 <>
Compute for the whole zodiac (or: for each sign) according to the day and the velocity. In 12 years you add 4;10, in 1,11 years you subtract 5, in 7,7 years the longitude (returns) to its original longitude.
The Babylonians possessed two sets of initial corrections assigned to the fast and the slow synodic arcs; the second correction in longitude given above (5;00 degrees) concerns the former; for the slow arc the correction was the 4;50 degrees above in association with the 71-year period relation. The full set of periods for Jupiter are given in ACT 813, Section 20 24 namely the intervals applied in Table 1 above of 12, 71, 83, 95, 166, 261 and 427 years (7,7) leading to a final integer period relationship of 36 sidereal revolutions, 391 synodic periods, a total sidereal motion for the 427-year interval of 36 x 360 degrees (3,36,0) and a mean synodic arc of 33;8,45 degrees as explicitly stated in ACT 813, Section 21:
"[ 7,7, years (corresponds to) 6,31 appearances ] 36 rotations, 3,36,0 motion. 33,8,[4]5 (is the) mean value of the longitudes."
Thus more simply in decimal notation and general terms 427 years corresponds to 391 mean synodic appearances, 36 sidereal revolutions, 12,960 degrees total sidereal progress and 33;8,45 degrees (rounded) for the mean synodic arc. In Neugebauer's terminology (ACT, pp. 282-283), the relationship is expressed as: N Years = II synodic "appearances" and Z sidereal "rotations" of 360 degrees, although the use of "rotation" in this context is fundamentally inappropriate given that the latter undoubtedly represent sidereal revolutions. Nor can there be any doubt that for the above to have any meaning the sidereal revolutions in question must unequivocably represent closed orbits, thus the revolutions must necessarily take place with respect to a specific centre, as indeed must the mean synodic arc for it to have any meaning whatsoever. To which may also be added the attested Babylonian awareness to within one degree of what we today recognize to be the line of apsides, along with the location of the line that corresponded to the mean values. At which point one begins to suspect that Neugebauer's claim that the Babylonians never possessed a fictive approach to planetary motion was not only premature, but also puzzlingly erroneous.
To continue, the mean synodic arcs for both Jupiter and Mars were apparently rounded at the third sexagesimal place (in the present case 33;8,45 = Z x 360 / II = 33;8,44,48,29,...degrees). It is generally understood that the number of mean synodic arcs (II) can be obtained from the relation: II = N - Z. The determination of the Final, or "long" babylonian period is therefore simply an intermediate step to firstly obtain mean values.

The next steps concern the detemination of the variable velocities and the variable times according to Babylonian System A or System B methodology. Expressed in synodic months, the synodic times for System B were also derived according to the convoluted method provided in Section 2 of Jupiter text ACT 812 25 involving thirtieths of the mean synodic month (tithis) and the Babylonian year of 12;22,8 mean synodic months (371;4 r ) split into two constants, k1 = 12 months (360 r ) and k2 = 11;4 r. Because the time required to travel one degree was taken to be 371;4/360 degrees = 1;1,50,40 r/o (Neugebauer, ACT, p.286 and p.393) the time for the mean synodic arc (u) would be: u(1;1,50,40) plus one year, or as explicitly given in Section 2 of ACT 812 , [u + u(0;1,50,40) +11;4 r +12 months]. This multiplicative process could have been applied each time the synodic arcs changed, but instead the segment [u(0;1,50,40)] was combined with k2 (11;4 r ) to form a fundamental constant (k3) which was added to both the mean and the varying synodic arcs with (presumably) acceptable marginal deviations in the results. Dividing by 30 and combining with k1 produces synodic times expressed in mean synodic months, i.e., u = 33;8,45 degrees, k3 = u(0;1,50,40)+11;4 = 12;5,8,8,20 r, thus 33;8,45 + 12;5,8,8,20 = 45;13,53,8,20 tithi = 1;30,27,46,16,40 months.  In other words, the mean synodic time for Jupiter expressed in mean synodic months is:
    [{(u+k3)/30}+k1] = 13;30,27,46,16,40 months.

Now fragments of Section 1 of ACT 812 explicitly mention the total number of synodic arcs (391) and also the value "13,30,27,46," -- an elementary parameter of far-reaching significance that Neugebauer apparently found to be "completely dark," even though he was but one simple step from it in Section 2 of the same text (see  above, and also ACT, pp.392-393). Thus the occurrence of this parameter in Section 1 clearly indicates that the mean synodic time can be derived simply and directly from the fundamental period relationship for Jupiter, i.e., from the relation: N = 427 Years, II = 391 mean synodic arcs, Z = 36 revolutions, i.e., 427 x 12;22,8 / 391 = 13;30,27,45,52,.. mean synodic months, which rounded-up at the third sexagesimal place gives the value provided in Section 1 of ACT 812 of "13;30,27,46."

This simple calculation employing the standard year of 12;22,8 mean synodic months is applicable to all the final Babylonian period relations:
SATURN: 265 Years, 256 Mean Synodic Arcs, 9 Sidereal Revolutions
Mean Synodic Arc = 9 x 360 / 256 = 12;39,22,30 Degrees (exactly)
Mean Synodic Time = 265 x 12;22, 8 / 256 = 12;48,13,26,15 Months

JUPITER: 427 Years, 391 Mean Synodic Arcs, 36 Sidereal Revolutions
Mean Synodic Arc = 36 x 360 / 391 = 33;08,45 Degrees (rounded)
Mean Synodic Time = 427 x 12;22, 8 / 391 = 13;30,27,46 Months (rounded)

MARS: 284 Years, 133 Mean Synodic Arcs, 151 Sidereal Revolutions
Mean Synodic Arc = (151 x 360 / 133) - 360 = 48;43,18,30 Degrees (rounded)
Mean Synodic Time= 284 x 12;22, 8 / 133 = 26;24,42,20,45 Months (rounded)

VENUS: 1151 Years, 720 Mean Synodic Arcs ( and 1871 sidereal revolutions )
Mean Synodic Arc = 1151 x 360 / 720 = 575:30 Degrees (exactly)
1151 x 12;22, 8 / 720 = 19;46,22,57,20 Months

MERCURY: 46 Years, 145 Mean Synodic Arcs ( and 191 sidereal revolutions )
Mean Synodic Arc = 46 x 360 / 145 = 114;12,24,49,40 Degrees (rounded)
46 x 12;22, 8 / 145 = 3; 55,26,7,30 Months (rounded)


Section 1 of ACT 812 therefore provides a simple, straight-forward method for obtaining the mean synodic periods expressed in mean synodic months, whereas the alternative (and more accurate) method in Section 2 provides the basis for both the mean and varying synodic parameters with the inclusion of the varying synodic arcs. Both are fundamental (if not primary) methods associated with the Babylonian approach to mean and varying planetary motion. Nevertheless, Neugebauer was unable to come to terms with the given constant in the first section, nor (for whatever reason) did he carry the methodology to its logical and necessary conclusion in the second section of ACT 812. Such fundamental deficiencies combined with Neugebauer's "linear" arithmetical approach to closed orbits, substitution of "rotations" for orbital revolutions, and not least of all, his failure to deduce an obvious System B for Mars from readily available data in procedure texts such as ACT 811 suggest that however erudite and qualified Neugebauer may have been, he was not particularly well-acquainted with the fundamental framework, and thus far from justified in his assertions that Babylonian astronomers possessed no cinematic approach to planetary motion. Moreover, in spite of the wealth of technical details in his 1955 opus Astronomical Cuneiform Texts, it is likely that his non-cinematic, non-model approach sadly rendered the Babylonian material largely unreadable on one hand and hardly worth reading on the other. Thus few uncommitted astronomers probably ever bothered to read the work, while the majority of those that did likely preferred to take Neugebauer's word rather than try to understand convoluted details discussed in base-60 without a cinematic model of any kind. Nevertheless, as it now stands, I would suggest that the cinematic, heliocentric nature of Babylonian astronomy was in reality self-evident ever since the publication of Astronomical Cuneiform Texts, at least for anyone who cared to tackle the material with sufficient industry and an open, inquiring mind.

IVb. BABYLONIAN "CHARACTERISTIC PHENOMENA" The Babylonian use of "characteristic" synodic phenomena appears to have been largely minimized and generally misunderstood by most modern commentators for reasons that are far from clear. It is certainly true that the phenomena in question are not generally treated by modern astronomers, but even so there are aspects of the methodology that require careful consideration--not least of all the twin components provided firstly by the diurnal axial rotation of Earth about its axis from west to east, and secondly--also from west to east--the annual revolution of Earth itself. "East" and "west" are therefore loaded terms, but they are nevertheless perfectly understandable in the Babylonian context, especially from the heliocentric viewpoint, as indeed are all the Babylonian synodic phenomena. Take, for example, the following description of the motion of Jupiter with elliptical planetary orbits viewed from above with both Jupiter and Earth moving "concentrically" around the Sun from west to east roughly in the same plane.
 Fig. 2. The relative sidereal motions of Earth and Jupiter
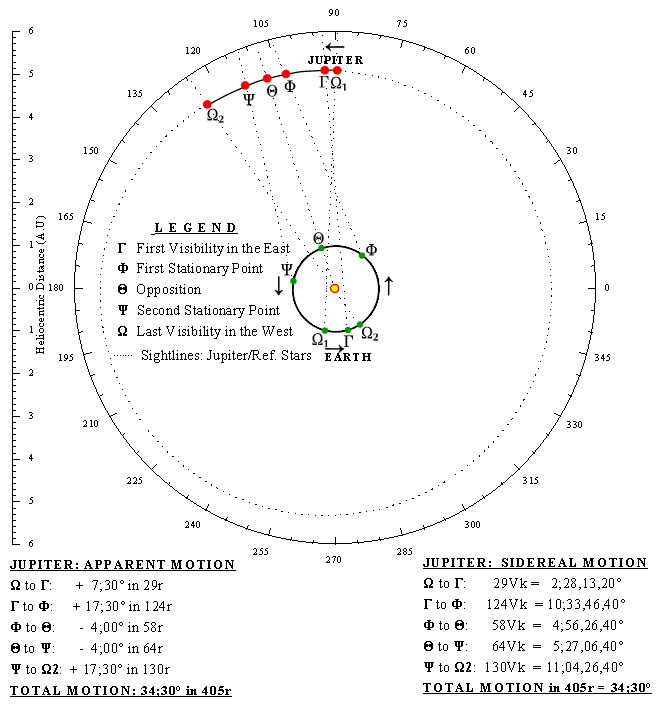
Fig. 2. The relative sidereal motions of Earth and Jupiter.

According to the procedures outlined in Sections 30 and 31 of ACT 813 (a lengthy Babylonian procedure text for Jupiter) starting with Jupiter positioned at 90 degrees and Earth at 257 degrees (say), as faster-moving Earth continues to move away from Jupiter there will eventually be a "Last Appearance (i.e., last visibility) in the West" for Jupiter when this planet becomes obscured from view, i.e., when Earth moves "behind" the Sun. The next time Jupiter will become visible will be the "First Appearance in the East" (after a further 29 days of motion by Earth) as Earth swings around the Sun and Jupiter becomes visible once again as it rises on the eastern horizon on one specific date (i.e., the helical rising). Next, as Earth continues to gain on Jupiter, it will reach a position (the "First Stationary Point")whereafter Jupiter will appear to move "backwards" and then reach opposition when Jupiter, Earth and Sun are in line. Further progress takes Earth to the "second Stationary Point" after which Jupiter's forward motion will apparently resume. Lastly, continuing to move away from Jupiter, Earth will once again reach a point in the orbit when Jupiter finally disappears from view, i.e., the "Last Appearance in the West" is reached again, and so on into the next cycle. All of which is perfectly understandable in heliocentric terms and almost meaningless without.
It is not certain whether sequential observations of this kind necessarily resulted in the Babylonian determination of the 12 and 71 year periods and ultimately the fundamental period relationship for Jupiter of 427 years with its 36 sidereal periods and 391 "First appearances in the East." But one thing seems clear enough; carrying out continued observations of successive synodic phenomena around the complete orbit of a planet against the background provided by the "goal-year" and other stellar reference points would naturally lead to an awareness of the faster, slower and mean orbital velocities and also where they were located. Thus it is not that difficult to envisage how the Babylonian were able to determine varying orbital velocity, the range between extrema, the rate of change and even the location of the line of apsides. Nor is it hard to see that in doing so and also coming to terms with the apparent retrogradation and stationary points, that the Babylonians had no need whatsoever for auxiliary devices. Their approach may have been a simple one, but it was the simplicity of Occam's Razor nevertheless, as the following detailed example shows:
Figure 3. The relative sidereal/synodic motions of Earth and Jupiter for the medium synodic arc.
3. The relative sidereal/synodic motions of Earth and Jupiter for the medium synodic arc.

SYNODIC MOTION
Referring to Figure 3, the elliptical orbits of Earth and Jupiter are displayed on a 360 degree sidereal reference frame with Jupiter initially at the 90 degrees at the point that corresponds to the synodic velocity of 34;30 degrees and Earth initially at 257 degrees. Fixed sidereal velocities of one degree per tithi for Earth and a velocity Vk = 34;30/405r = 0;5,6,40 degrees per tithi for Jupiter produce the positions for the Babylonian "characteristic" phenomena over one complete synodic cycle for Jupiter and the specific synodic arc in question. The example may perhaps shed some light on the puzzling statement found in ACT 814 (Sect. 2, L9): "for the first station it is high, for the second station it is low" in so much as the synodic velocity that started at 34;30 degrees falls to almost 34 degrees by the time the second stationary point is reached. Needless to say, the above also shows that such phenomena as stationary points and retrograde motion are clearly apparent and it is undoubtedly direct orbital motion that is under consideration throughout. Thus for mean values, because of the fundamental period relationship for Jupiter, the Mean synodic arc (u) = (Zx360)/II and Mean synodic time = (Nx12;22,8)/II, unit time per degree is therefore obtained from: (Nx12;22,8)/(Zx360) = N/Z(1;1,50,40).r/o In the case of Jupiter, this parameter (unit time per degree) is: (427/36)(1;1,50,40) r/o = 12;13,32,46,40r/o or 12.0344361337...days per degree, which is unquestionably the sidereal motion of Earth for each degree of Jupiter's sidereal motion. Moreover, Babylonian fundamental period relations for Mars and Saturn also produce corresponding times for the motion of Earth. For example, from the full Babylonian period relationship for Saturn of 265 years, 256 mean synodic arcs and 9 periods of revolution, the mean synodic arc of 9x360/256 =12;39,22,30 degrees Saturn takes 12;48,13,26,15 months and thus the planet moves 0;2,0,30,11,42,... degrees per day. Thus dividing the latter into one sidereal revolution of 360 degrees results in 10,754;53,47,35,41,... (10,754. 89655...) days to complete one mean sidereal period. The further division of this total by the number of days in the standard 12;22,8-month Babylonian year next produces 29;26,40 (29.444* years), the attested Babylonian mean sidereal period for the planet in question. On the other hand, the Babylonian fundamental period relationships for the two inferior planets (Mercury and Venus) provide only the number of years (N) and the number of synodic occurrences (II). This would seem to be one of the two the major factors which have hitherto mitigated against a fictive understanding of the Babylonian approach to planetary motion; the other is the apparent motion of the Sun in both planetary and luni-solar contexts. Yet these two factors are necessarily related and the motion of the sun in Babylonian astronomy need be no more indicative of Babylonian theoretical basis than is our own retention of solar motion for computational convenience (i.e., the slow, mean, and fast sun applied to the equation of time, etc). Thus, as Zombeck (1993) explains in a modern astronomical treatise on the motion of the moon: 26

"It would be natural but impractical to describe the motion of the moon in heliocentric coordinates. In the method used here to determine the position of the moon we shall consider that both the Sun and the Moon are in orbit about Earth. The position of the Sun was calculated in Section 2.1 under this assumption, and we shall use these calculations to correct the mean orbital elements of the moon for solar perturbations."(emphases supplied)

With respect to the planets, from a distinctly fictive heliocentric viewpoint, the sidereal motion of an outer superior planet provides the synodic arc, while the sidereal motion of the inner planet (Earth) supplies the unit of time. In the case of the inferior planets, from the same heliocentric viewpoint, Earth is now the outer planet, therefore its motion provides both the synodic arc and the synodic time, which renders the numbers of sidereal periods for Mercury and Venus completely superfluous. In other words, the number of years (N) in the period relationships for the latter pair is also the number of revolutions (Z) of Earth. Even though the Babylonian treatment of planetary phenomena pertains to synodic rather sidereal velocity, on further examination the approach is nonetheless found to represent direct, forward sidereal motion per unit time. Finally, with Earth in motion, the relations: 12;22, 8 / 360 = 1;1,50,40 r/oand N x 12;22, 8 / II apply consistently to the known Babylonian fundamental period relations, as shown with largely decimal values for simplicity in the following table:
 
PLANET
N
Z
II
T = N/Z
Synodic Arc
Synodic T1
Synodic T2
Degrees/day
SATURN
 265 9  256 29.444444 12.65625 12.80373 378.10183
0;02,00,11,30,42
JUPITER   
427 36  391 11.861111 33.14578 13.50771 398.89077
0;04,59,08,29,37
MARS     
284 151  133 1.8807947 408.72180 26.41176 779.95505
0;31,26,31,01,24
VENUS    
1151 1871  720 0.6151791 575.50000 19.77304 583.90971
0;59,08,09,04,37
Mercury 1
46 190  144 0.2421053 115.00000 3.95117 116.68048
0;59,08,09,04,37
Mercury 2
46 191  145 0.2408377 114.20690 3.92392 115.87579
0;59,08,09,04,37
Mercury a
848 3521  2673 0.2408407 114.20875 3.92399 115.87767
0;59,08,09,04,37
Mercury b
388 1611 1223 0.2408442 114.21096 3.92406 115.87991
0;59,08,09,04,37
Mercury b2
480 1993  1513 0.2408430 114.21018 3.92404 115.87912
0;59,08,09,04,37
Mercury d
217 901  684 0.2408435 114.21053 3.92405 115.87947
0;59,08,09,04,37
Table 2. Babylonian Period Relations

NOTES
N is the number of years in the final integer period relation.
Z is the corresponding number of mean sidereal periods, i.e., number of complete sidereal revolutions.
II is the corresponding number of mean synodic arcs and corresponding mean synodic periods.
T = N/Z = The mean sidereal period in years, i.e., one sidereal revolution.
Synodic Arc = The mean synodic arc in degrees (decimal notation).
Synodic T1 is the mean synodic time expressed in mean synodic months (decimal notation).
The mean synodic time is expressed in days (decimal notation).
The mean synodic month provides the standard unit of time, i.e., the constant of 29;31,50,8,20 days
The mean synodic arc for Mars is given in full; the applied value is the excess over  1 x 360 degrees.
The corresponding motion of Earth (with respect to that of Mars) is the excess over 2 x 360 degrees.
For a more accurate set of hypothetical period relations for VENUS see Appendix B.
The mean sidereal periods for the two inferior planets (in parenthesis) are implicit.
The identical degrees/day for the inferior planets results from the mean motion of Earth.

METHODOLOGY
The periods and velocities in Table 2 above are derived from the integer elements of Babylonian fundamental relationships, i.e., the integer parameters N, Z and II.  The resulting periods and velocities are impressive, even though the mean synodic arcs for both Jupiter and Mars were rounded by the Babylonians from 33;8,44,48,29,. to 33;8,45 degrees for the former, and further reduced for the latter to the excess over one revolution, i.e., 408;43,18,29,46,27,.. minus 360 to obtain the mean arc of 48;43,18,30 degrees. This modification notwithstanding, the complete synodic arc and resulting mean synodic period for Mars nevertheless still provide the correct motion for Earth expressed in degrees per day. The standard unit of time in all cases was the Babylonian "year" of 12;22,8 mean synodic months, which may also be treated as the time required for Earth to complete one sidereal revolution of 360 degrees. This corresponds to the daily motion of Earth of 0;59,8,9,04,36,59,.degrees associated with the period relationships for the two inferior planets as explained above.  The sidereal periods for the latter pair are implicit in the relationships, and although not required they may still  be obtained from the standard relation ( Z = N + II ), i.e.,
Z = Number of Years N + Number of Synodic Periods.
The period relationships for Mercury concern either the general statement (2) "145 phenomena of the same kind in 46 years," or specific observational phenomena given in ACT (pp.283-288), i.e., from the following:
( a )  "2673 appearances as a morning star" ( First visibility in the east )
( b )  "1223 disappearances as a morning star" ( Last visibility in the east )
( b2) "1513 appearances as an evening star" ( First visibility in the west )
( d )  "684 disappearances as an evening star" ( Last visibility in the west )


 Fig. 4. The six observational points for Venus and Mercury

The less accurate Mercury relationship from ACT 816 (i.e., No. 1) appears to represent a pedagogical simplification associated with the determination of a "System B" type variable velocity function. In this case the extremal velocities would be m = 97;00 degrees and M = 133;00 degrees. With the same value for the difference d, the extremal velocities for the 46-year/145 arc relationship would be in turn: 96;04,54,49,4 degrees and 132;19,54,49,40 degrees respectively.
It may be remarked that none of the final data for Mercury and Venus necessarily reflect observational periods per se, any more than do those of the superior planets. In fact it seem possible that the entire corpus of planetary relations based on the T1:T2 pairings could have been generated over perhaps a century or less, though this need not be taken as indicative of the comparative newness of Babylonian astronomy on one hand or the limits of their inquiries on the other. They are simply fragments of what have come down to us. How extensive was Babylonian astronomy? How far back in time did it extend and what else remains? Short of additional material these questions may remain unanswered, although there are undoubtedly intriguing aspects that still defy explanation, especially a strangely ignored mathematical problem concerning a trapezoid that occurs in Jupiter procedure texts ACT 813 and ACT 817 (see below), along with still unknown corrections and parameters in the luni-solar texts.

SUMMARY [ 1997 ]
Whether one accepts what has been discussed here or not, it should at least be recognized that complex issues arising from precession, the various types of months, and the definition of the "year" merely represent the luni-solar component of Babylonian astronomy while further questions arise from the limited number and uneven distribution of the planetary texts published in ACT and elsewhere. In fact, there would appear to be sufficient gaps and uncorrelated parameters to suggest that Babylonian astronomy was almost certainly more developed than is usually assumed. Included in this latter group are unexplained parameters and operations in the planetary texts and unknown corrections for both the solar velocity 27 and the zodiac 28 in the lunar material. One might also consider the implications of the extensive range of the Babylonian period relations, synodic phenomena in association with varying, direct, and retrograde velocity, closed orbits, lines of apsides, and not least of all, the aforementioned trapezoid in two astronomical procedure texts for Jupiter.29 (For further details see Otto Neugebauer's minimal treatment of the trapezoid in Astronomical Cuneiform Texts (single-page PDF, 34 kb).
Given the undoubted awareness of accurate sidereal periods for the superior planets, implicit sidereal periods for the inferior planets, accurate sidereal, synodic, draconic, and anomalistic months, and varying velocity functions for the planets, sun, and moon - all readily understood in terms of a cohesive framework - it seems reasonable to conclude that the Babylonians almost certainly possessed a well-developed, fictive heliocentric planetary model by 250 BCE at the very latest, and quite possibly much earlier.

REFERENCES
1. Neugebauer, O. Astronomical Cuneiform Texts (Lund Humphreys, 3 Vols, London, 1955).
2. Neugebauer, O. A History of Ancient Mathematical Astronomy (Springer-Verlag, Berlin, 1975).
3. Van der Waerden, B. Science Awakening II The Birth of astronomy, with contributions by Peter Huber (Oxford University Press, New York, 1975).
4. Astronomical Cuneiform Texts, Ed. O. Neugebauer (Lund Humphreys, London, 1955)404.
5. Harris, J. Letter to the Editor of ISIS, Vol. 68, No.245, December 1977:626-617.
6. Astronomical Cuneiform Texts, Ed. O. Neugebauer (Lund Humphreys, London, 1955) 414.
7. Manitius, K. Ptolemaus Handbuch Der Astronomie (B.G. Teubner, Leipzig, 1963)100.
8. Duncan, A. On the Revolutions of the Heavenly Spheres (Barnes and Noble, New York, 1976) 235-236.
9. Newton, R. The Crime of Claudius Ptolemy (Johns Hopkins University Press, Baltimore and London, 1977).
10. Newton, R. The Origins of Ptolemy's Astronomical Parameters (Technical Report No. 4, Center for Archaeoastronomy, College Park, Maryland, 1982).
11. Newton, R. The Origins of Ptolemy's Astronomical Tables ( Technical Report No. 5, Center for Archaeoastronomy, College Park, Maryland, 1985).
12. Goldstein, B. Al-Bitruji: On the Principles of Astronomy (Yale University Press, New Haven London, 1971)
13. ACT 210, Section 3, Astronomical Cuneiform Texts (Lund Humphreys, London, 1955) 271-273.
14. Op. cit., p. 272.
15. Neugebauer, O. A History of Ancient Mathematical Astronomy (Springer-Verlag, Berlin, 1975) 503.
16. Op. cit., p.518.
17. ACT 210, Section 3, Astronomical Cuneiform Texts (Lund Humphreys, London, 1955) 272.
18. Hartner, W. "The Young Avestan Calendar and the Antecedents of Precession," JHA, Vol X (1979) 1-22.
19. Neugebauer, O. Astronomical Cuneiform Texts (Lund Humphreys, London, 1955) 70.
20. Aaboe, A. "A Seleucid Table of Daily Solar (?) Positions" Journal of Cuneiform Studies, Vol. 18 (1964) 34.
21. Sachs, A. "The Goal-Year Texts," Journal of Cuneiform Studies Vol. 2 (1948).
22. Neugebauer, O, and A. Sachs. "Some Atypical Astronomical Cuneiform Texts I," Journal of Cuneiform Studies, Vol. 21 (1967) 183-218.
23. ACT 813, Section 1, Astronomical Cuneiform Texts (Lund Humphreys, London, 1955):403-404.
24. ACT 813 , Section 20, Astronomical Cuneiform Texts (Lund Humphreys, London, 1955):414-415
25. ACT 812, Section 2, Astronomical Cuneiform Texts (Lund Humphreys, London, 1955):393-394.
26. Zombeck, M. Astronomical Formulas, Section 2.2, MATHCAD Electronic Books, (MathSoft Inc., 1993.).
27. ACT 200, Sections 7 and 9, Astronomical cuneiform Texts (Lund Humphreys, London, 1955) 193-195, 198.
28. ACT 202, Section 2, Astronomical Cuneiform Texts (Lund Humphreys, London, 1955) 242-244.
29. ACT 813, Section 5, Lines 1-4, ACT 817, Section 4, Lines 1-12, Astronomical Cuneiform Texts, 405; 430-431.
30. Hoyrup, Jens. Lengths, Widths, Surfaces: A Portrait of Old Babylonian algebra and its Kin (Springer-Verlag, New York,2002).
31. Robson, Eleanor. Mathematics in Ancient Iraq: A Social History (Princeton University Press, New Jersey, 2002).
33. Friberg,Jöran. Unexpected Links between Egyptian and Babylonian Mathematics (World Scientific Publishing, Singapore, 2005).
34. __________  A Remarkable Collection of Babylonian Mathematical texts (Springer, New York. 2006).
35. __________  Amazing Traces of a Babylonian Origin in Greek Mathematics (World Scientific Publishing, Singapore, 2007).
36. Davis, Linda. Technical Mathematics with Calculus (Merrill Hill, Columbus, 1990).
37. Swerdlow, Noel M. The Babylonian Theory of the Planets. (Princeton University Press, Princeton, 1996).

SUPPLEMENTARY INFORMATION I
Babylonian Mathematics and Sexagesimal Notion: Comments and a few examples.

Copyright © 1997. John N. Harris, M.A.(CMNS).  Last updated on May 1, 2012.

APPENDIX A
HYPOTHETICAL BABYLONIAN PARAMETERS FOR URANUS

THE NAKED-EYE VISIBILITY OF URANUS

Preliminary Remarks:

1. URANUS, discovered fortuitously by William Herschel with the aid of a telescope in 1781 is unquestionably visible to the naked eye1, 2 ,3 
2. As Wagner [1991] has pointed out, it is in fact surprising that URANUS was not detected in antiquity.4 
3. Babylonian astronomers - long skilled in observing planetary risings and settings etc., would have been prime candidates for the incidental discovery of a faint (but visible) outer planet moving in essentially the same orbital plane as Mars, Jupiter and Saturn.
4. If detected, URANUS could well have been subjected to the same Babylonian procedures adopted for the three attested superior planets, leading to the eventual determination of the corresponding planetary parameters discussed below.
5. Hypothetical Babylonian parameters for URANUS (Systems A and B) are given below for comparison with values that may be encountered in the future.

I. MEAN VALUES
As discussed in detail above, the final Babylonian fundamental period relationships for the three known superior planets appear to have depended on two initial integer periods (T1 and T2) thaty are close to the mean sidereal periods (or multiples thereof) for which small, convenient corrections for longitude of opposite sign were determined; leading in turn to the final integer period when the corrections completely cancel out. 
for example, (using Neugebauer's terminology from ACT, pp.282-283), the relationship for Jupiter was expressed as: N Years = II synodic "appearances" and Z sidereal "rotations" of 360 degrees, but in so much as the mean synodic arcs for both Jupiter and Mars were rounded at the third sexagesimal place, and that of Saturn was exact. (265 Years = 256 synodic appearances and 9 sidereal revolutions; mean synodic arc u = 9 x 360 / 256 = 12;39,22,30 degrees) is would appear that both accurate and rounded values were applied. Either way, however,what will be required in the case of Uranus are initally the two periods T1 and T2 (with attendant corrections in longitude) that will provide the final integer relationship Tn. Thus, based on a period of revolution of Uranus of approximately 84 years, for example, the initial pairs of periods with the requisite corrections in longitude leading to the final period relation can be suggested:
T1 = 81 Years, = 80 synodic arcs and 1 sidereal revolution of 360 degrees -10;00 degrees
T2 = 85 Years, = 84 synodic arcs and 1 sidereal revolution of 360 degrees + 7;30 degrees
leading to a final integer period relationship for Uranus of Fn = 583 years as follows:
T1 = 81 Years, 80 synodic arcs, 1 revolution of 360 degrees - 10;00 Degrees
T2 = 85 Years, 84 synodic arcs, 1 revolution of 360 degrees  + 7;30 Degrees
T3 = 166 Years, 164 synodic arcs, 2 revolutions of 360 degrees - 2;30 degrees (T1 + T2)
T4 = 251 Years, 248 synodic arcs, 3 revolutions of 360 degrees + 5;00 degrees (T2 + T3)
T5 = 417 Years, 412 synodic arcs, 5 revolutions of 360 degrees + 2.30 degrees (T3 + T4)
FN = 583 Years, 576 synodic arcs, 7 revolutions of 360 degrees and 0;00 degrees correction (T3 + T5)
thus, according to standard methodology, the hypothetical mean values for Uranus based on a final period Fn of 583 years would be in turn:
Mean Sidereal Period = N/Z = 583/7 = 83.28571428 Years
Mean Synodic Period = N/II = 583/576 = 1.01215277 Years
Mean Synodic Period (months) = 583 x 12;22,8 Months / 576 = 12;31,9,8,20 Mean Synodic Months
Mean Synodic Arc (u) = N x 360 / II = 7 x 360 / 576 = 4;22,30 degrees
[ Mean Heliocentric Distance:  19.0713 A.U.]


ADDITIONAL OPTIONS
Other possibilities include final period relations of:

a.  249  years (3 sidereal revolutions)
b.  420  years (5 sidereal revolutions)
c.. 565 years  (7 sidereal revolutions)
d.  586 years  (7 sidereal revolutions)
e.  587 years  (7 sidereal revolutions)
f.   589 years  (7 sidereal revolutions)

with intermediate periods, corrections, and mean parameters (u is the value of the mean synodic arc in degrees) as follows:
f. N = 589 Years, Z = 7, II = 582
Mean Sidereal Period T = 84.14285... Years
Mean synodic arc u = 4;19,47,37,43,..(4;19,45 rounded?)
Mean Heliocentric Distance:  19.2019 A.U.
T1 = 82 Years (360 - 9;10)
T2 = 85 Years (360+ 3;40)


e. N = 587 Years, Z = 7, II = 580
Mean Sidereal Period T = 83.85714... Years
Mean synodic arc u = 4;20,41,22,45,..(4;20,40 rounded?)
Mean Heliocentric Distance:  19.1584 A.U.
T1 = 81 Years (360 - 12;15)
T2 = 85 Years (360+ 4;54)

d. N = 586 Years, Z = 7, II = 579
Mean Sidereal Period T = 83.71428... Years
Mean synodic arc u = 4;21,08,23,37,..(4;21 rounded?)
Mean Heliocentric Distance:  19.1367 A.U.
T1 = 83 Years (360 - 3;00)
T2 = 84 Years (360+ 1;12)

c. N = 565 Years, Z = 7, II = 559
Mean Sidereal Period T = 80.71428... Years
Mean synodic arc u = 4;30,58,03,52,..(4;31 rounded?)
Mean Heliocentric Distance:  18.6767 A.U.
T1 = 80 Years (360 - 3;10)
T2 = 81 Years (360+ 1;16)

b. N = 420 Years, Z = 5, II = 415
Mean Sidereal Period T = 84 Years
Mean synodic arc u = 4;20,14,27,28,..(4;20,15 rounded?)
Mean Heliocentric Distance:  19.1802 A.U.
T1 = 81 Years (360 - 12;45)
T2 = 86 Years (360 + 8;30)

a. N = 249 Years, Z = 3, II = 246
Mean Sidereal Period T = 83 Years
Mean synodic arc u = 4;23,24,52,40,..(4;23,20 rounded?)
Mean Heliocentric Distance:  19.0277 A.U.
T1 = 81 Years (360 - 8;40)
T2 = 84 Years (360 +4;20)

NOTES: The selection of the above periods was partly influenced by 589 and 83-year Jupiter period relations in Babylonian "Goal-Year" texts ( the latter period is also the sum of Jupiter T1 = 12 years and Jupiter T2 = 71 years).

The corrections for the 583-year period are based on information in a lunar text (ACT 210, Section 2) found in a line preceding the possible mention of the 265-year fundamental period for Saturn. The fragmentary condition of the section and the absence of a second correction make this insecure data doubtful. Nevertheless, the resulting 583-year period provides a convenient mean synodic arc of 4;22,30 degrees, which is generally in keeping with attested Babylonian mean values for the other visible superior planets (Mars, Jupiter and Saturn).

Less likely data based on a 565-year final period (7 sidereal revolutions; mean synodic arc: 4;30,58,3,52,..) owes its origins to the unexplained occurrence of the number "4 31" found in an early Babylonian text concerned with "omens" associated with a cryptic reference to a moving "star" in the constellation of Pisces, i.e., "If the Fish Star approaches the Acre Star..." with the latter considered to be in the adjacent constellation Pegasus.

The  mean heliocentric distances range from 19.202 A.U. through 18.677 A.U.
The average value is 19.064985 A.U. Both this value and that of the 83-year period round conveniently to 19.


II. HYPOTHETICAL SYSTEM A PARAMETERS FOR URANUS
Based on modern aphelion and perihelion distances, Babylonian System A synodic arcs for Uranus might perhaps center around 4;20 degrees for the mean value with  4;2 degrees and 4;40 degrees for "Slow" and "Fast" arcs distributed over 200 and 160 degrees respectively, i.e., as applied in the case of Saturn. Or alternatively, around 4;00 and 5;00 degrees with a corresponding mean synodic arc (u) closer to 4;30 degrees, etc.  Finally, for a mean synodic arc of precisley 4;31 degrees the corresponding times for various approximations would be:
1. 12;31,26,39,41,20 months (k = 11,12,19,50,40)
2. 12;31,26,40 months for k = 11;12,20 r
3. 12;31,26 months for k = 11;12 r.


III. HYPOTHETICAL SYSTEM B VELOCITIES FOR URANUS

BASIS: THE 583-YEAR INTEGER PERIOD RELATIONSHIP FOR URANUS:

N = 583 YEARS, II = 576 SYNODIC ARCS, Z = 7 SIDEREAL REVOLUTIONS

P = Number of mean synodic arcs per sidereal revolution = 360/u
T = Sidereal Period = P + 1
d = Increase/decrease in velocity (degrees) and time (tithi) per synodic arc = 0;1,10
Amplitude of Synodic Arcs = 1/2Pd = 0;48 (1/4Pd = 0;24)
m = Minimum Synodic Arc: ( u - 1/4Pd)  = 3;58,30 degrees
u = Mean Synodic Arc: [(7 x 360 )/576]  = 4;22,30 degrees
M = Maximum Synodic Arc (u +1/4Pd)   = 4;46,30 degrees
The 583-year period is used here for simplicity. The attested determination of the mean synodic arc (u) from the division of the total sidereal motion by the number of synodic arcs in the final relationship would be followed by the derivation of the parameters of a "linear zigzag" function given above and below. The difference, d = 0;1,10 is on the high side, but closer to the approximate 9 : 1 ratios of the Mars : Jupiter and the Jupiter : Saturn differences. Values for this parameter might range from 0;40 to perhaps 0;1,20. (note: The derivation of the extremal velocities follows the procedure suggested by the remnants of Section 1 of Jupiter procedure text ACT 812 )


IV. HYPOTHETICAL SYSTEM B TIMES FOR URANUS
(a) SYNODIC FACTORS IN TITHIS (Synodic Arc + k3 = Synodic Arc + 11;12,4,10,r Abbreviated value: +11;12 r )
(m) = 15;10,51,40 r Minimum Synodic Arc (abbreviated value: 15;10,30 )
(u ) = 15;34,34,10 r Mean Synodic Arc (abbreviated value: 15;34,30 )
(M) = 15;58,16,40 r Maximum Synodic Arc (abbreviated value: 15;58,30 )

 (b) SYNODIC PERIODS (MONTHS) [ IV (a) Values/30 + 12 Mean Synodic months]
(m) = 12;30,21,43,20 mean synodic months
(u ) = 12;31,9,8,20 mean synodic months (369.699569 days)
(M) = 12;31,56,33,20 mean synodic months
The synodic times in tithis and mean synodic months were derived according to the method given in Section 2 of Jupiter text ACT 812 (Neugebauer, Astronomical Cuneiform Texts, Lund Humphreys, London 1955:393). The mean synodic time for Uranus is also obtainable from the final integer relationship and the methodology indicated in Section 1 of the same text, i.e., the mean synodic time is accordingly:

583 x 12;22,8 / 576 = 12;31,9,8,20 mean synodic months (of 29;31,50,8,20 days).

V. THE SELEUCID ERA
The Seleucid Era - a Babylonian astronomical era of unknown significance - begins with Month 0, Year 0 in April 310 BC (311 BCE). As it so happened, Uranus was occluded three times by Jupiter around this time, i.e., on September 23, 312 BCE, January 2, 311 BCE ( Uranus at opposition and nearly at its brightest, M = +5.4 ) and April 29, 311 BCE, i.e., April 310 B.C. Those with astronomical software can observe from the location of Babylon (Iraq: 44 25E, 32 33N) the positions of both planets, the perceptible parallax exhibited by Uranus with respect to Jupiter between the dates given and the planet's later motion (at its brightest) along the ecliptic through the constellation of Leo.


SUMMARY
Firstly, because of the relatively low visual magnitude of Uranus it is possible that even if sighted the orbit could not be completely determined.

Secondly, although no unambiguous references to an additional planet are apparent in the historical record there nevertheless remain enigmatic statements and parameters of unknown significance in both earlier Babylonian material and the astronomical cuneiform texts of the Seleucid Era.  Moreover, complex issues arising from "precession", the various types of months, and the definition of the "year" represent the luni-solar component of Babylonian astronomy which is itself in need of additional research from a dynamic viewpoint.

Others issues arise from the limited number and uneven distribution of the extant planetary texts. In fact, sufficient gaps and uncorrelated parameters remain to suggest that Babylonian astronomy was quite likely more developed than is normally assumed.

Until the matters outlined above and at the end of the parent paper are addressed more adequately, it would surely be premature to dismiss the capabilities of Babylonian astronomers, or their possible naked-eye detection of Uranus, conventional wisdom and the status quo notwithstanding.


APPENDIX B
HYPOTHETICAL PERIOD RELATIONS FOR VENUS AND MERCURY

B1: VENUS

PRELIMINARY REMARKS
In general, it may be assumed that shorter Babylonian period relationships will provide less accurate mean values than those obtained from F, the Final (and exact) integer period relationship determined from the initial T1 and T2 periods, e.g.,

F = 284 Years, 133 Mean Synodic Arcs, 151 Orbital Revolutions [MARS]
F = 427 Years, 391 Mean Synodic Arcs,  36 Orbital Revolutions [JUPITER]
F = 265 Years, 256 Mean Synodic Arcs,   9 Orbital Revolutions [SATURN]
F = 583 Years, 576 Mean Synodic Arcs,   7 Orbital Revolutions [URANUS(?)]

However, for Mercury and Venus no corresponding T1 and T2 periods are readily apparent; furthermore, in the case of Venus the 1151-year relationship yields a relatively poor value for the mean synodic period. Nor, for that matter, does the corresponding mean synodic arc inspire confidence, being simply one half of the period itself (i.e., 1151*360/720 = 1151/2 = 575;30 degrees). The latter may well be a working value, and a convenient one at that, but with a length of 1151 years for the final integer period one might reasonably have expected more accurate results. Recalling, however, the key period relations for Jupiter provided in Section 1 of ACT 813 (see above) 23
"Compute for the whole zodiac (or: for each sign) according to the day and the velocity.
In 12 years you add 4;10, in 1,11 years you subtract 5, in 7,7 years the longitude (returns) to its original longitude."
(In 12 years you add 4;10 degrees, in 71 years you subtract 5 degrees, in 427 years the longitude returns to its original longitude)
and the expansion that produced the attested period relation for Jupiter of:

427 years, 391 mean synodic arcs and 36 sidereal revolutions

Table.1 Babylonian Period Relations and the 427-year Period for Jupiter

Table.1 Babylonian Period Relations and the 427-year Long Period for Jupiter

one could do little more than hope that additional periods for Venus and Mercury might eventually come to light from newly recovered cuneiform tablets etc., and failing this, from other historical sources.

THE 243-YEAR PERIOD I
In the latter category, for example, there is the interval of 243 years mentioned in the following cryptic footnote by George Burges (1876:171):

 . . . .   the ratio of  243 to 256  is to that of  35 to 44; especially if we bear in mind what is stated by Plutarch,
De Anim., Procreat. ii, p. 1028, B., respecting Lucifer (Venus) being represented by 243, and the Sun by 729.
(George Burges, The Works of Plato, George Bell and Sons, London, 1876:171) 10

THE 8-YEAR PERIOD 
Although it may seem an unnecessary elaboration " the ratio of 243 to 256 is to that of 35 to 44 " may also be restated as: " the ratio of  243 to 256  is to that of 35 to 28 ", but apart from the well-known Venus/Fibonacci relationship of 5 synodic periods, 8 years and 13 orbital revolutions, little in the way of additional understanding follows. But this is numerology in any case, is it not? Possibly, but it is more likely methodology, and highly condensed methodology at that. But in any event, the parent work itself is found in "The Treatise of Timaeus the Locrian" in Burge's The Works of Plato (1876) whereas initial references to the number "243" occur in a distinctly "Pythagorean" context, i.e., in a footnote to Burge's own SUPPLEMENTARY NOTE to (yet another extension) "The Notes of Batteaux." However, since we are not so much concerned here with Pythagorean tenets as the determination of fundamental period relations for Venus the latter subject is perhaps best left for a more specialized treatment at another time.
Nevertheless, it might still be unwise to "criticize without light."

 
THE 251-YEAR PERIOD; ADDITIONAL COMPLEXITIES  
So far so good, though merely the 8-year Venus cycle with its 5 corresponding synodic periods and 13 corresponding orbital revolutions, and an obscure historical reference to an interval of 243 years. What next? As far as my own efforts were concerned, nothing at all. It was in fact the Internet that supplied the answer, providing both intermediate periods T1, T2 as well as F, the final"long" integer relationship in one neat, detailed package. The source in question, however, dealt with matters far more difficult than the present historical asterisk, namely the complexities that arise from the analysis of the transits of Venus carried out by Karl-Heinz and Uwe Homan. For present purposes, however, the following periods discussed in detail by the latter ( VENUS TRANSITS AND PRECESSION, May 31, 2004):
A preliminary analysis of the Venus Transit Data has shown that the Earth must go around the Sun 360 degrees in a tropical year, contrary to current lunisolar precession theory. The fact remains and the evidence suggests that the observed transit cycles reflect a more accurate correlation between the periods of 251 tropical years and 408 orbits of Venus around the Sun, than 243 and 395 respectively. 
This paper examines what appears to be a pattern of resonance between Venus transit cycles, the mean synodic period and the time interval of the 360-degree tropical year based on Earth's non-precessing axis of rotation relative to the position of the Sun.  .... A complete 360-degree cycle occurs after 157 mean synodic periods, or exactly 251 tropical years and 408 orbits of Venus.
( Uwe Homan, The Sirius Research Group, May 31, 2004; emphases suppplied)

plus the 5, 152 and 157 Venus synodic periods and corresponding 13, 395 and 408 orbital periods applied in an earlier paper (TRANSITS OF VENUS VS NASA'S ASTRONOMICAL DATA, April 21, 2004) provide all that is necessary. In these modern contexts the latter sets are discussed in detail with respect to both the tropical year and the sidereal year with far-reaching implications; in our present historical context, however, all six periods may simply be used directly after the manner adopted for Jupiter, i.e., hypothetically:

"In 8 years you add 1;26,  In 243 years you subtract 1;26.
 In 251 years the longitude (returns) to its original longitude."

Table 2. Hypothetical Babylonian Period Relations and the 251-year Long Period for Venus

Table 2.  Hypothetical Babylonian Period Relations for Venus
Final Period F = 251 years, 157 mean synodic arcs and 408 orbital revolutions.

In Table 2 the longitude corrections of 1;26 degrees are conveniently truncated from the more accurate value of 1;26,3,20,47,48,..(1.434262948.. degrees); the positive correction the excess over 360 degrees after 8 years, the negative correction the amount less than 360 degrees after 243 years.These corrections necessarily involve the annual orbital motions of Earth and Venus, the latter value being 585;10, 45,25,5,58,33,( 585.179282868. degrees from the 251-year relationship, i.e., from 408 x 360 / 251).
   Finally, though not to be confused with the modern complexities that attend this matter, the mean synodic period for Venus (based on the Babylonian year of 12;22,8 mean synodic months) can be otained from the final period as before, i.e.,

 251 x 12;22,8 / 157 = 19;46,28,4,35,9, (19.774465676...) mean synodic months, or simpler still: 19;46,30 months.

B2: MERCURY

13-YEAR AND 33-YEAR PERIODS
Although a similar situation exists for Mercury, i.e., no attested T1 and T2 periods or related Final Period (F), the available material for this planet is nevertheless more extensive. However, remaining with the better known 46-year period that has come down to us in various planetary theories (e.g., those of Ptolemy, Al-Bitruji, and Copernicus) the methodology applied in the case of Venus -- apart from the reversed polarity of the paired corrections -- remains virtually unchanged, i.e.,

"In 13 years you subtract 7;50,  In 33 years you add 7;50.
 In 46 years the longitude (returns) to its original longitude."

Table 3. Hypothetical Babylonian Period Relations for Mercury

Table 3.  Hypothetical Babylonian Period Relations for Mercury
Final Period F = 46 years, 145 mean synodic arcs ( 191 orbital revolutions )

Here again the longitude corrections (7;50 degrees in this instance; to two sexagesimal places perhaps: 7;49,30 ) are simplified variants of more accurate values obtainable from the 46-year final relationship ( i.e.,  7;49,33,54,46,57, ...,  7.826086956 .. degrees) and the combined annual orbital motions of both Earth (360 degrees) and Mercury (1494;46,57,23,28,41,44, ... degrees, etc.). In this case, however, the negative correction is the amount less than 360 degrees for T1 (13 years) and the positive correction the excess for T2 (33 years).  Based on the final 46-year integer relation the mean synodic period will accordingly be:

46 x 12;22,8 / 145 = 3;55,26,7,30 months (3;55,26,7,26,53,47..) or more approximately, 3;55,30 months.

REFERENCES
1. Moore, Patrick.Naked Eye Astronomy, W.W. Norton, New York, 1965
2. Webb, Rev. T.W. Celestial Objects for Common Telescopes, Dover, New York, 1962:221.
3. Levy, D H. THE SKY - A User's Guide, Cambridge University Press, Cambridge 1991:134.
4. Wagner, Jeffrey K. Introduction to the Solar System, Holt, Rinehart and Winston, Orlando 1991.
5. ACT 813, Section 1, Astronomical Cuneiform Texts, (Lund Humphreys, London, 1955..
6. Horowitz, W. "Two New Ziqpu-Star Texts and Stellar Circles,"Journal of Cuneiform Studies, Vol 46, 1994.
8. Gadd, J. "Omens Expressed as Numbers," Journal of Cuneiform Studies, Vol 21.1967.
9. Van Der Waerden, B. Science Awakening II, Oxford University Press, New York, 1974.
10 Burges, George. The Works of Plato: A new Literal Verson, George Bell and Sons, London, 1876.

Added July 3, 2004. Links and text updated April 3, 2009.

mailto: john_harris@shaw.ca

Return to spirasolaris.ca