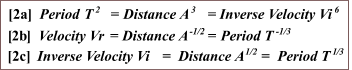PART II. THE ALTERNATIVE
A. CONSIDERATIONS AND COMPLICATIONS
1.
GENERAL CONSIDERATIONS
2.
SOLAR SYSTEM PLANETS
3. THE INTER-MERCURIAL OBJECT
B. ORBITAL AND LINEAR
REPRESENTATIONS
1.
NORMAL AND LOGARITHMIC
PLANVIEWS
2.
LOGARITHMIC LINEAR REPRESENTATIONS
C. TIME AND MOTION
1.
SYNODIC MOTION AND
SYNODIC "ORBITS"
2. MEAN
ORBITAL VELOCITIES
3. INVERSE VELOCITY RELATIONS
D.
CONSTANTS OF LINEARITY
1.
THE SYNODIC FORMULA AND PLANETARY
SPACINGS
2. DETERMINATION OF THE
FUNDAMENTAL CONSTANT OF LINEARITY
3. RELATED CONSTANTS AND FORMULAS
E. ADDITIONAL TABLES AND GRAPHICS
1. RELATED PHEIDIAN CONSTANTS AND FORMULAS
A.
CONSIDERATIONS AND COMPLICATIONS
A1.
GENERAL CONSIDERATIONS
Although we
are perhaps still too close to judge the matter effectively, the
apparent
lack of progress in coming to terms with the overall structure of the
Solar
System since the Titius-Bode era suggests that the latter's ad hoc
approach was in all likelihood more of an impediment than a help, and a
long-lived impediment at that. With this in mind it therefore seems
necessary
to seek a wider yet more critical approach to the matter--specifically
an approach that: (a) avoids preconceptions and ad hoc
methodology
and (b), an approach that necessarily incorporates an increased
planetary
database beyond that restricted to mean heliocentric distances alone.
But
although the inventory of the Solar System has been enlarged and
refined
over the past two centuries, fundamental difficulties nonetheless
remain.
In particular, even if it should prove feasible to approximate the
present
planetary structure, it may still not be possible to account for the
many
anomalies that currently exist within the Solar System. Here one
necessarily
includes such things as origins, changes over time, and also the
possibility
of occasional catastrophic events, periodic or otherwise. But even
without
such considerations the absence of a standard frame of reference for
planetary
systems per se means that we currently have no way of knowing
whether
the Solar System represents the norm for planetary systems, an evolving
or modified form of the latter, or (for whatever reason) even an
exception
to
the rule.
A2. SOLAR SYSTEM PLANETS
Although oddities and
exceptions abound
throughout the Solar System and the mechanisms involved remain beyond
our understanding, we can at
least take stock of the System as we know it today. Thus we may begin
with
the generally accepted division of the nine planets into two main
planetary
groups. In due order outwards from the Sun then, are firstly the
innermost
solid planetary bodies known as the Terrestrial Planets, i.e., Mercury,
Venus, Earth and Mars. Beyond the last named lies the Asteroid Belt and
beyond this massive Jupiter, the largest of the nine planets and the
innermost
of the Four Gas Giants--Jupiter, Saturn, Uranus and Neptune. Lastly,
out
beyond Neptune in a class of its own and in an unusual orbit lies tiny
Pluto--a
body so small that even as a moon it would still rank no higher than
the
fifth largest
moon in the Solar System.
Thus from a
preliminary
viewpoint there are essentially four distinct regions--the
first
occupied by the relatively small Terrestrial Planets, the second by the
Asteroid Belt, the third by the four immense Gas Giants and lastly the
remote and singular domain of tiny Pluto. Here one can at least begin
to
regroup the data, for it is questionable whether Pluto is necessarily a
planet at all, even though it may be occupying a planetary "position"
per
se . But what constitutes a planetary position in this context
anyway,
given that we have no established planetary framework to guide us?
About
all that can be suggested at this stage is that Pluto, though still
part
of the planetary set represents an anomaly that may or may not be
explained
by further investigation. Next, a second anomaly of a different kind
would
seem to be the Asteroid Belt, but while there are over 5,000 asteroids
in the region and others beyond it, their combined masses (Ceres
included) are
nevertheless
far too small to account for a planet per se. But was there ever
a planet between Mars and Jupiter? Again, we simply do not know; but
then
neither do we know what caused so many asteroids to be in this
particular
region in the first place, though various hypothetical scenarios
involving
collisions and/or the gravitational break-up of planets have been
proposed
(notably by Tom Van Flandern;1
see
also the latter's Exploded
Planet Hypothesis - 2000). But here matters increase in complexity,
for orbital shifts and the redistribution of planetary masses
necessarily
affect the total angular momentum of the Solar System, rotational
component
of the Sun included. Which brings us to a third anomaly, namely that
although
the Sun has by far the greatest mass, it is the planets--predominately
the Four Gas Giants--that possess almost all of the angular momentum.
Thus
postulating orbital changes and/or the break-up of hypothetical planets
between Mars and Jupiter (or indeed anywhere in the System) involves
mathematics
of N-body proportions and complexity. Difficult enough for a single
occurrence,
what then of other events that may or may may not have been sequential,
periodic, or alternatively, totally unrelated in both time and place?
As
for the early historical side of the matter, there are also problems
and
unanswered questions that pertain to the precedence of planetary
formation
itself, i.e., to what extent the Gas Giants may have preceded the
Terrestrial
planets, and whether the Asteroid Belt and/or the orbit of Pluto
preceded
or followed the formation of the Terrestrial Planets in turn, etc. Here
once again the matter of origins comes to the fore, as does the
possibility
of catastrophic events and relatively large-scale changes within the
Solar
System itself. All of which suggest that the first and foremost
requirement
is an underlying planetary structure--not necessarily complete in its
entirety
either, but useful enough to provide a valid starting point and an
initial
frame of reference for further analysis.
But
where
then
to begin? Perhaps with planet Earth itself, not least of all because it
is
the
mean parameters of Earth that provide the fundamental frame of
reference
for
Solar System distances, periods,
velocities, and planetary masses, etc. Next,
notwithstanding the recent (2006) demotion of Pluto and elevation of
the asteroid Ceres to the status of "Dwarf Planets," the present
analysis -- though occasionally including the latter pair -- will
primarily concentrate on the following two major groupings (parameters relative to
unity):

Table
1. The Two Primary Groupings of Solar System Planets
1.
Planetary masses include satellites and atmospheres
2. Mean
Heliocentric Distances in Astronomical Units
(A.U).
3. Mean
Periods of Revolution in Years (Harmonic Law:
ref. unity).
4. (e)
Eccentricities.
5. Angular Momentum (L) from MVi
(Mass x Inverse Velocity)
6. Dwarf Planets Pluto, xxx, xxx (2006)
omitted
Additional data, i.e.,
physical
composition, orientation of planetary
axes and planes of revolution, densities and gravities, etc., could
also
have been included the above, but such data remain difficult to
separate
from
the early formation of the planetary structure itself, with or without
subsequent modifications. More in keeping with the present approach and
the need to enlarge the available database we may on the other
hand add to the attested planets an Inter-Mercurial Object
(hereafter IMO) that
owes its origins to orbital parameters
determined
by Leverrier. Reported in the journal Nature 4
in 1876, the "object" (mean period: 33.0225 days,
corresponding
mean distance 0.201438 A.U.) lies between Mercury and the Sun as the
title
implies. Thus for present purposes it serves to extend the
range
of planetary mean distances at the innermost extremity, which is not to
suggest that the object is/was necessarily a planet per se, but
rather (subject to reservations already stated above) an object that
may
or may not be occupying a planetary location. This step is in fact a
minor
addition that although helpful is not vital to the development of the
final
framework or the enlarged database; in fact the latter results largely
from the inclusion of mean periods and mean velocities in critical
contexts
that will be discussed in detail later. However, before moving on to
this
stage further groundwork remains; specifically, the reevaluation of the
manner in which planetary orbits and parameters are generally
represented.
B. ORBITAL AND LINEAR
REPRESENTATIONS
B1. NORMAL AND LOGARITHMIC
PLANVIEWS
In retrospect, the suggestion
of an exponential component in the structure of the Solar System
implied
in the Titius-Bode relationship might reasonably have been explored
with
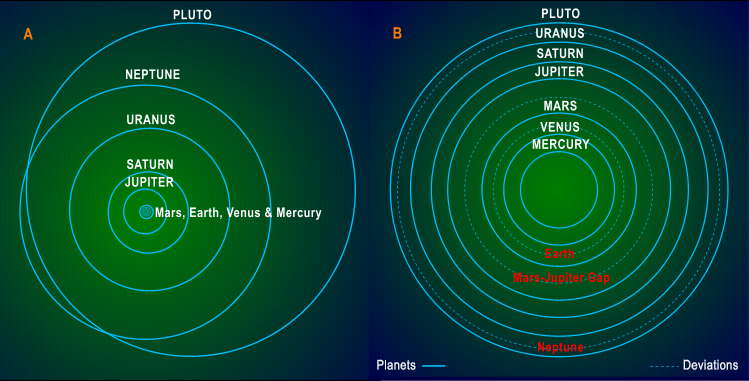
far more rigor and forethought than appears to have been the case. The planview
of the
Solar System could surely have been examined more closely
from a logarithmic viewpoint, especially since the deficiencies of
normal planview representations have long been known. In fact,
although it may not be
immediately
obvious, it is particularly beneficial to represent Solar System orbits
logarithmically
since the three innermost terrestrial planets (Earth,
Venus
and Mercury) can scarcely be discerned using normal values and normal
means
of presentation (see Figure 1a). On the other hand,
logarithmic
ranges in such applications effectively "compress" the outermost values
and
"expand" the inner, providing an informative and revealing view of
the
entire Solar System as shown in
Figure 1b:
Figure
1a. Elliptical Orbits,
Normal Scale.
Figure 1b.
Mean Distance
Orbits, Logarithmic Scale
Clearly, from the second
representation alone the presence of an exponential element might be
suspected which in turn gives to an initial regrouping Apart from
its convenience
this representation of the mean value orbits
also suggests that:
Figure
1c. Mean Distance Orbits IMO-NEPTUNE
Figure 1d. The Two Log-Linear Zones
B2.
LINEAR LOGARITHMIC REPRESENTATIONS
Given that the
Harmonic (or Third) law of planetary
motion -- the cube
of
the mean heliocentric distance A equals
the square
of the mean sidereal period
of revolution T
--
is
itself exponential:

Relations
2g, 2t and
2r: The Third or Harmonic Law
it would obviously be
advantageous to treat mean planetary
data
logarithmically. Relative to unity--the
fundamental frame of reference based provided by the mean parameters of
planet Earth ( the exponential set:1
:
1 : 1 :
1 )
the mean
orbital
velocities (Vr) of the planets range from approximately
1.6
to 0.16 (actual values: 1.6072 to 0.1609);
the mean heliocentric distances (A) range from
approximately
0.39
to 39 A.U. (0.387 to 39.45 A.U.) and the
mean
periods of revolution (T) range from approximately
0.24
to 240 years (0.2408 to 248.081 Years ). Thus
the
three sets of mean values fall into convenient exponential ranges of 10,1
10,2
and 10.3
In other words, the decadic expansion: 1 : 10 : 100 :
1000, whereas the
first and second
integer sets (other than unity) that demonstrate the Harmonic Law are
similarly the Double and Triple
expansions 1 :
2 : 4 :
8 and 1
: 3 : 9 :
27. In any
event, the third law and
the Solar System may readily be
represented
logarithmically (e.g., Figure 2 and variants below;
see also Zeilik2, p.63, and a
logarithmic
x-axis representation of the mean distances by Nieto
3). In other
words, logarithmic linear representations furnish useful visual
indicators and practical baselines, especially since
the resulting
exponential representation is a straight line
and successive exponential positions are all equi-spaced.
Thus the
following
3-cycle/2-cycle logarithmic exposition of the Harmonic Law includes the
latter for the arithmetic progression 1, 2, 3, ...100, and
also the exponential function F(a) = 2 x (x = 0, 1, 2,
3, ... 6):
Figure
2: The Straight-line Logarithmic Representation of the Harmonic Law (1
to 100 A.U. / 1 to 1000 Years)
Continuing with the
preliminary
indications provided by Figure 1b and the suggestion made in Part I,
the
planet-to-planet
increases for Earth and Mars may both be atypical, with Earth
possibly
occupying an "intermediate" position between Mars and Venus. In Part I
it was not possible to discuss the matter in further, but here mean
values provide further frames of reference, or more
properly,
indexes of the proximity of adjacent planets and a tentative reference
frame for the mean distances. In other words, values that are
greater
than the mean may serve to indicate that the body in question is further
out from the Sun than the "theoretical" norm (i.e., the position
corresponding
to the log-linear framework), while values that are lower are
correspondingly
nearer
the Sun, etc. Thus in practice, Venus may be considered to be slightly
closer to the Sun, while Mars (because of the Venus-Mars and Earth-Mars
increases) considerably further out. Similarly, both Uranus and Pluto
may
also be considered to be beyond the "norm", while Neptune--already
suspected
of occupying an "intermediate" position--may be much closer in.
Moreover,
the increases for the two
exceptions
(Earth and Neptune) are not only similar in value, they also appear to
be reversed. Here, of course, matters are complicated by the
possibility
(if not the fact) that the distances for the neighboring planets
(i.e.,
Mars in the inner zone and Uranus in the outer) may also deviate
somewhat
from the "norm" for whatever cause or reason. About all that
can be said at present is that these preliminary indications remain
simply
that.

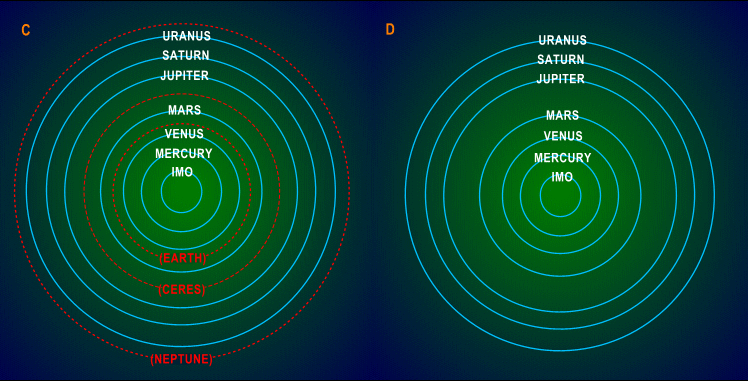
Figure
2b. Planetary positions in the Two Log-Linear Zones (IMO omitted)
Apart from its convenience
this representation of the mean value orbits
also suggests that:
- A degree of linear
separation (i.e., log-linearity) may exist in the
spacings
of the majority of the planets in the Solar System.
- In particular,
log-linearity appears to be present among the three
adjacent
planets Jupiter, Saturn and Uranus in the Gas Giant Zone.
- Further, log-linearity
also appears to be present among the three
Terrestrial
Planets Mercury, Venus and Mars in the Terrestrial Zone, IMO included.
- Although no planet
exists in the Mars-Jupiter Gap, the Mars-Jupiter (and/or Ceres)
mean
matches the spacing between the two log-linear zones.
- Possible deviations
from both log-linear sequences are suggested by the
orbits of Earth in the inner zone and that of Neptune in the outer.
With respect to the latter possibilities, the "kink" in Bode's Law
discussed
in Part I has already engendered the suggestion that Earth may be
occupying
a "synodic" (i.e., intermediate) position between Venus and Mars.
Similarly,
from Figure 1b Neptune may perhaps be occupying
an "intermediate" or "synodic" position between Pluto and Uranus. If
so,
then Pluto (though still an errant moon rather than a planet per se)
may in turn be occupying the next planetary position beyond Uranus.
Although the preliminary
possibilities
suggested by the log-linear representation of the Solar System are
little
more than that at present, the latter approach nevertheless provides
further
avenues for investigation. In particular, the mean distances can now be
reexamined in terms of the Solar System planet-to-planet increments
discussed
in Part I, but from a narrower viewpoint with a correspondingly sharper
focus. Thus the planet-to-planet multiplication factors shown below
concentrate
primarily on the two suggested log-linear zones while the distances and
attendant multiplication factors for Earth and Neptune provide similar
exceptions.
What is required next is the
introduction of synodic motion and
orbital
velocity, after which the suspected deviations and anomalous locations
of Earth, Neptune and the Mars-Jupiter Gap may be revisited and
examined
in further detail.
C. TIME AND MOTION
C1. SYNODIC
MOTION
Although the majority of attempts
to come to terms with the structure of the Solar System have largely
been concentrated on mean heliocentric distances, it seems
likely--especially in view of the limited amount of progress to
date--that
more tools and more data were and are required. Given the known
relationship
between
mean distances and mean periods inherent in the third law of planetary
motion (see relations 2g, 2t and 2r below)--it therefore seems
reasonable
to include the mean periods of revolution, though this step requires
a further expansion before it becomes usable in the present context.
What is required is something that
binds the planets
together,
and for this purpose synodic periods and planetary velocities now enter
into
the discussion, i.e., if the planets are indeed ordered, then the
manner
in which they move with respect to each other should also be ordered,
and any ordering that involves the distances necessarily also involves
both
the periods and the orbital velocities. Which means,
because of
the exponential relationships
that exist between all three, that the two latter sets of parameters
should also be
available for present purposes.
C2. THE
GENERAL SYNODIC FORMULA
In more detail, although
rarely
described in the following form, for any pair of co-orbital bodies
(where
T2 denotes the period of revolution of an outer body, T1
the period of revolution of an inner body, and T2 > T1) the general synodic
period (or "lap" time) may be expressed as the product of the two
sidereal periods (T1
and T2) divided by their difference:
Relation
1a: The
General Synodic Formula
Here the mean parameters of
Earth provide the standard frame of reference (unity). The synodic
periods
of the planets are more commonly given with respect to the relative
motion
of Earth using simpler formulas. The latter variants are, however,
merely special cases of Relation 1a with unity (the
sidereal period of Earth) replacing T1 or T2
according to which group of planets is under consideration. Relation 1a
is also further simplified by implicit multiplication (i.e., by
unity: 1 x T2 = T2, etc.) such that the
standard synodic formulas are usually expressed separately.
C3. MEAN SYNODIC
CYCLES
 With the motion and mean
parameters of Earth providing
the
fundamental frame of reference for
planetary mean distances, mean periods and mean velocities it
now proves
possible to extend the investigation to include synodic cycles between
each adjacent planetary pairing in the Solar System. For example, in
simple
terms, in the cases of the first three gas giants the synodic cycle of
Jupiter with respect to Saturn (i.e., Jupiter's lap-cycle) is
approximately
20 years while that of Saturn with respect to the next planet (Uranus)
is approximately 45 years. Thus the two synodic periods
lie neatly between
the sidereal periods of the bracketing planets in both cases. But what
of the synodic
cycle of Uranus with respect to Neptune, the latter planet already
suspected
of occupying a synodic location? In this case the synodic cycle turns
out
to be greater than that of Neptune itself. It is natural,
therefore
to wonder if the same situation prevails in the case of the other
suspected
anomaly, i.e., the position of Earth and therefore the synodic cycle of
Earth with respect to Mars. Here once again the synodic period turns
out
to be greater than that of the
outermost planet in the pairing. But
this
is not all, for the two suspect planets Earth and Neptune now show a
further
anomaly, namely that the synodic cycles on either side of these
two planets are larger than
the sidereal period of the planet itself
(see
Table 3). A double coincidence? Perhaps, perhaps not, especially when
the
remaining synodic cycles are all found to follow a consistent yet
different
pattern, i.e, for the Terrestrial planets from IMO to Venus and the
first
three Gas Giants the intervening synodic periods each lie between
their associated bracketing planets. Moreover, if we do consider that
Earth
might be occupying the synodic position between Venus and Mars, then
the
Terrestrial Planets sequence can be extended by two additional steps
with
the inclusion of Mars. But even without this extension and IMO it seems
that two similar log-linear regions might exist in the present Solar
System--the
first involving the three successive periods from Mercury to Venus
(five
with the inclusion of Mars), and the second from Jupiter to Uranus once
again involving five successive periods.
With the motion and mean
parameters of Earth providing
the
fundamental frame of reference for
planetary mean distances, mean periods and mean velocities it
now proves
possible to extend the investigation to include synodic cycles between
each adjacent planetary pairing in the Solar System. For example, in
simple
terms, in the cases of the first three gas giants the synodic cycle of
Jupiter with respect to Saturn (i.e., Jupiter's lap-cycle) is
approximately
20 years while that of Saturn with respect to the next planet (Uranus)
is approximately 45 years. Thus the two synodic periods
lie neatly between
the sidereal periods of the bracketing planets in both cases. But what
of the synodic
cycle of Uranus with respect to Neptune, the latter planet already
suspected
of occupying a synodic location? In this case the synodic cycle turns
out
to be greater than that of Neptune itself. It is natural,
therefore
to wonder if the same situation prevails in the case of the other
suspected
anomaly, i.e., the position of Earth and therefore the synodic cycle of
Earth with respect to Mars. Here once again the synodic period turns
out
to be greater than that of the
outermost planet in the pairing. But
this
is not all, for the two suspect planets Earth and Neptune now show a
further
anomaly, namely that the synodic cycles on either side of these
two planets are larger than
the sidereal period of the planet itself
(see
Table 3). A double coincidence? Perhaps, perhaps not, especially when
the
remaining synodic cycles are all found to follow a consistent yet
different
pattern, i.e, for the Terrestrial planets from IMO to Venus and the
first
three Gas Giants the intervening synodic periods each lie between
their associated bracketing planets. Moreover, if we do consider that
Earth
might be occupying the synodic position between Venus and Mars, then
the
Terrestrial Planets sequence can be extended by two additional steps
with
the inclusion of Mars. But even without this extension and IMO it seems
that two similar log-linear regions might exist in the present Solar
System--the
first involving the three successive periods from Mercury to Venus
(five
with the inclusion of Mars), and the second from Jupiter to Uranus once
again involving five successive periods.
Before proceeding with the next
stage is seems necessary to emphasize
that although the mean synodic periods represent difference or lap
cycles
between successive pairs of adjacent co-orbital planets, such cycles
nevertheless
represent complete revolutions of 360 degrees per mean synodic period.
The difference between this type of orbital motion and planetary
revolutions
per
se is that the latter take place with respect to a fixed sidereal
reference
point, whereas the former take place with respect to a moving point of
reference. Even so, for every such mean synodic period the concept of
an
equivalent
sidereal period and equivalent synodic "orbit" can be applied. With
this
device applied consistently throughout, the equivalent synodic orbits
may
then be included in log-scale representations of the Solar System. Here
the results serve to emphasize the log-linear aspect far more
effectively
than the numeric representation provided in Table 2. In fact, omitting
both Neptune and Pluto for the time being, the suggestion of
log-linearity
appears to be quite pronounced whether planet-to-planet, synodic-to
synodic,
or indeed sequentially (i.e. planet-synodic-planet) in the two
log-linear
zones under consideration (see Figures 2c, 2d and 2e). Although no
planet
can be assigned to the Asteroid Belt per se, an orbit that
corresponds
to the geometric mean between Mars and Jupiter (2.8156896 A.U.,
sidereal
period: 4.7247945 years) also provides bracketing synodic periods
similar
to those of the Terrestrial and Gas Giant zones, if not the
continuation
from the latter to the former. Not included in the table but shown in
Figures
2c and 2d is the Venus-Mars synodic of 0.914222 years that lies just
inside
to the mean orbit of Earth. Omitted for clarity from the Figures 2c and
2d are the Earth-Mars and Mars-Jupiter synodics with mean periods
of 2.135375 years and 2.234902 years respectively that lie just beyond
the
orbit
of Mars.
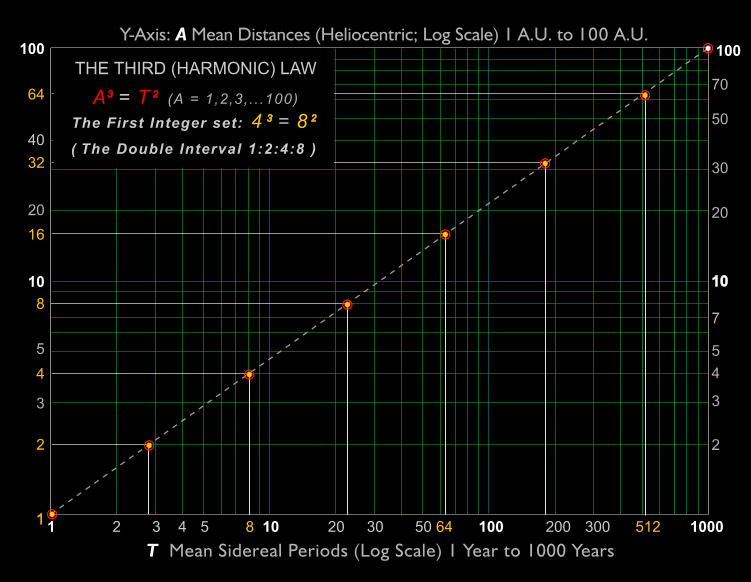
Figure
1e. Mean Planetary and
Mean Synodic Orbits.
Figure 1f.
Synodic
orbits in the Two Log-Linear Zones

Figure
2i. The Two Log-Linear Zones plus the Intermediate Synodic Periods
C4.
MEAN
ORBITAL VELOCITY
The next step
in the inquiry involves the inclusion of mean orbital velocity where
perhaps
surprisingly (perhaps not), enlightenment is provided by Galileo's
research
into projectile trajectories and his logical (albeit thinly veiled)
expansion
of the topic to include planetary motion and planetary origins.5 A detailed account of the
matter
need not be given here since it is sufficient for present purposes to
provide
the following expansions of the laws of planetary motion, specifically
the extension of the Third (or
Harmonic)
Law of Planetary motion to include mean
orbital velocity as follows: 5
Relations
2a-2c: Velocity
Expansions of the Harmonic Law
Once again such relationships
serve to emphasize that if the mean
distances
of the planets are indeed ordered, then the manner in which the planets
move with respect to one another, and thus the mean periods and the
mean
velocities should also be ordered. Which in a sense means that with
these
new additions the major orbital parameters available for analysis in
the present context have
been effectively quadrupled. The use of the Inverse
Velocity in
this context may appear unusual at first acquaintance, but it is a
useful
device nevertheless, not least of with respect to the computation of
angular momentum. Moreover, as will be seen next, the inverse velocities also
provide a linkage between the two log-linear zones.
C5.
INVERSE VELOCITY RELATIONS
During the preliminary phase
of the present investigation, relations [2b] and [2c]
were
instrumental in bringing to light that fact there presently exist in
the
Solar System an unusual pair of of inverse-velocity relationships that
serve to
connect
the two suspected log-linear zones. The precise details need not be
given here, but in essence:
Vi Venus
- Vi Mercury approximates
the mean velocity of the planet Uranus
Vi Saturn - ViJupiter approximates
the mean velocity of the planet Mars.
Vi Saturn/Uranus Synodic - ViJupiter/Saturn
Synodic approximates the mean velocity of the
Venus-Earth
synodic cycle
Figure
3: Inverse Velocity Relationships between the Superior and Inferior
planets
The inclusion of
Earth in
this
context--synodic location notwithstanding--thus
serves to augment the linkage between the terrestrial planets of the
lower
log-linear zone and three adjacent gas giants of the outer zone, (
Jupiter,
Saturn and Uranus.) One or two other inverse-velocity
relationship also appear to exist
that are almost sequential--a necessary qualifier in so much as
the
latter appear to incorporate synodics and planetary inverse
velocities. Although
mean values are applied in the above relationships, in real
time
such functions will obviously vary according to the elliptical natures
of the
associated
orbits. Real-time investigation of the Mars-Jupiter-Saturn
relationship
with frames of reference provided by the mean orbital velocity of Earth
of 29.7859 kilometers per second and 24.1309 kilometers per second for
that of Mars revealed that the real-time maxima and minima for Relation
[4b] range
between 19.66 and 28.3 kilometers per second, thus well exceeding the
extremal
velocities of Mars
itself. However, utilizing the methods
of Bretagon and Simon7 adapted to generate
sequential data for 5-day intervals from 1700 to 2000 A.
D.,
the
mean
value nevertheless still turns out to be 24.0938 kilometers
per second.
C6.
VARYING INVERSE VELOCITY
Similarly, the data for the
real-time function based on Relation [4s1]
reveals that although there is an even wider swing in extremal values,
the mean value is also comparable to that obtained from Relation [4s1]
directly. All of which is further complicated by the proximity of the
Mars-Jupiter
synodic to the Earth-Mars synodic and various resonances known to exist
in the Solar System -- complications that at this stage no doubt
intrude
rather than enlighten and as such will be deferred until later.
Figure
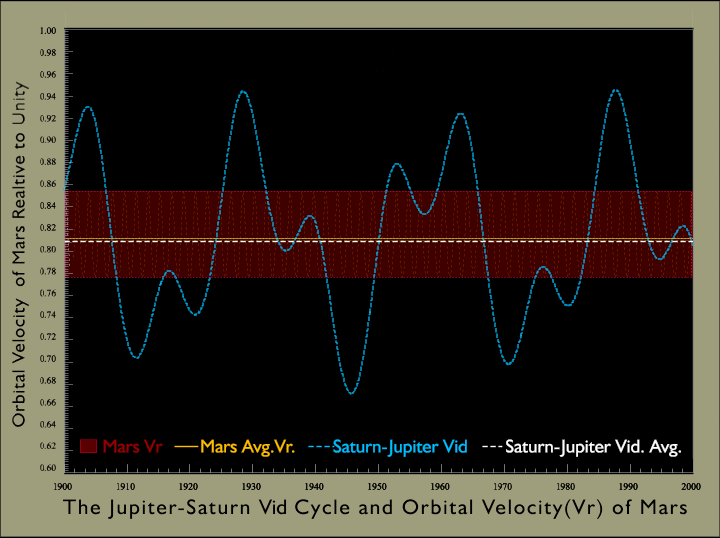
4. The Jupiter-Saturn Vid Cycle and Orbital Velocities of Mars
Finally, suffice it to note here
that although only a few inverse-velocity
relationships are readily apparent in the Solar System and this
scarcity
might suggest such relations have little to do with the log-linear
sequences,
it turns out that they are in fact an integral feature with
corresponding
values for all
planetary and synodic positions. The reason for there
being
so few obvious relations would appear to lie in the fact that the
inverse-velocity
relationships
are influenced in no small way by deviations in the planetary
structure.
Thus with three suspected deviations in the Solar System to contend
with it is perhaps
fortunate
that those that were evident were sufficient to connect the two
log-linear zones in the manner discussed above.
Summarizing the investigation
so far, there are indications -- despite of a number of anomalies --
that
the
Solar System may possess two log-linear zones separated by the Asteroid
Belt. With the addition of the intervening synodic periods and the
inverse-velocity
relationships, it can be tentatively suggested that there are
essentially
five consecutive inter-related periods in the outer zone, and (with IMO
included) five more in the inner zone, or with the further inclusion of
Mars, seven.
Fundamental questions that
remain
are the validity of the inverse-velocity relations themselves, what
assistance
they might render in the determination of the log-linear framework and
whether or not a single unifying log-linear function can be derived
that
connects the outer and inner log-linear zones.
D. CONSTANTS OF
LINEARITY
D1. THE
SYNODIC FORMULA AND PLANETARY
SPACINGS
The fundamental
question that remains to be answered is whether
an exponential component exists in the structure of the Solar System.
This
is certainly suggested
by the near log-linear spacings of the sidereal and synodic periods for
the
inferior planets (Mercury and Venus) and similar spacings further out
among
the adjacent superior planets Jupiter, Saturn and Uranus. Moreover, a
related
question that arose above was whether the trio of unexpected
inverse-velocity
relationships linking the outer and inner log-linear regions were
residuals
of the same suspected exponential structure, the possibly anomalous
locations of
Earth,
Neptune and Pluto notwithstanding.
It is fortunate
in one sense yet unfortunate in another that
the suggestion of log-linearity in two separate regions of the
Solar
System and the complex linkage provided by the inverse-velocity
relationships
impose rigid requirements on any exponential function that might
connect
the two.
In particular, an
exponential function for the mean periods
(both
sidereal and synodic) in the form F (x) = Mtk
x
(where Mt is a base constant provided by the mean sidereal
period of Mercury) must not only produce the three inverse-velocity
relationships
in the same order, it must also generate a complete exponential
planetary
framework that commences with the mean sidereal period of Mercury for x
= 0, thereafter sequentially generate the Mercury-Venus synodic
(Ts) for x = 1, followed by the mean
sidereal
period of Venus for x = 2, and so on.
Furthermore, if as
suggested in the first two parts, Earth is indeed occupying the synodic
location between Venus and Mars, then the position for Earth must
necessarily
be obtained from the next exponent (3), followed by exponent 4 for
Mars.
Moreover, from the log-linear representations demonstrated in Part II
it
is clear that sufficient spacing exists to incorporate a planetary
position
in the Mars-Jupiter Gap itself and also synodic locations on either
side.
Together these three positions should therefore account for exponents
5,
6 and 7. This leaves the successive mean sidereal and mean synodic
periods
for Jupiter through Uranus to be generated in turn by exponents 8
through 12, with results that should also produce
inverse-velocity
relations comparable to those exhibited in the Solar System. Lastly, if
IMO
(the
Inter-Mercurial Object) is indeed occupying a valid planetary
position,
then the function should also be expandable in the
opposite direction
and thus include both the latter's mean sidereal period and the IMO-Mercury
synodic for exponents
-2 and -1 respectively. Or, (and
even simpler) since the latter is uncertain, a continuous
exponential
function for the mean periods commencing with Mercury (Mt) that
connects the two log-linear zones
utilizing
sequential exponents that run from 0 through 14:
D2. THE
DETERMINATION OF THE FUNDAMENTAL CONSTANT OF LINEARITY
Thus, commencing with a base
provided
by the mean sidereal period of Mercury, i.e., Mk 0
=
M,
the
next position (Mk 1 )
corresponds to the
Mercury-Venus Synodic (
Mk1),
followed in due order by the mean sidereal
period
of Venus from Mk 2. Fortunately, because of general
synodic formula [1]:

the first expansion Mk1
is directly obtainable
from
The
product of the mean sidereal periods of Mercury ( Mk 0
=
M
) and
Venus (
Mk 2)
divided by their difference:

This leads directly to the
determination
that the value of k
for the successive sidereal and synodic periods of the exponential Solar System is
none other than the
constant Phi =
1.6180339887949, the "Golden Section" known and revered
since antiquity, defined in turn (Livio,
2002) 8 by the quadratic equation that
results from Relation
1b.

Figure 2g. The Exponential
Period Function F(x)
= Mtk x
( x = 0, 1, 2,..,14 )
D3. RELATED PHEIDIAN CONSTANTS AND FORMULAS
From
the above result it
is apparent that the mean periods of revolution and
intervening synodic periods increase sequentially by successive powers
of Phi itself, (essentially the Phi-Series)
while the
mean periods
of the planets increase in turn by Phi squared
with corresponding constants for the mean heliocentric distances and
mean orbital velocities both readily obtained from the Harmonic
Law and the velocity variants discussed earlier, i.e.,

Relations
5a-7b.
The Primary Pheidian Constants for the Mean Periods, Distances and
Velocities
In the next section
the latter series, the inverse velocity relations
and the
exponential planetary
frameworks will be explored more fully in terms of similarities,
deviations, and
multiple fibonacci/Lucas resonances in the present Solar System.
REFERENCES
- Van Flandern, Tom. Dark Matter, Missing planets and New Comets
,
North Atlantic Books, Berkeley 1993, 1999.
- Zeilik, M. Astronomy and the Evolving Universe, Harper
and Row,
New York, 1976.
- Nieto, M.M., "The Titius-Bode Law and the Evolution of the Solar
System," Icarus
25 (1974) 171-174.
- Leverrier, M, "The Intra-Mercurial Planet Question," Nature 14
(1876)
533. [Anon.]
- Harris, J. "Projectiles,
Parabolas, and Velocity Expansions of
the Laws
of Planetary Motion," Journal of the Royal Astronomical Society
of
Canada,
Vol. 83, No.3 (June 1989):207-218.
- Galileo, G. Dialogues Concerning The New Sciences,
translated
by
Henry Crew and Antonio de Salvio, Dover, New York, 1954.
- Bretagnon, P and Jean-Louis Simon, Planetary Programs and
Tables
from
-4000 to +2800, Willman-Bell, Inc. Richmond, 1986.
- Livio,
M. The Golden Ratio. The Story of Phi, The World's Most
Astonishing Number, Broadway Books, New York 2002.
Copyright © 1997.
John N. Harris, M.A.(CMNS).
Last Updated on March 9, 2007
PREVIOUS
I Bode's Flaw
http://www.spirasolaris.ca/sbb4a.html
Bode's "Law" - more correctly the Titius-Bode relationship - was an
ad hoc scheme for approximating mean planetary distances that was
originated by Johann Titius in 1866 and popularized by Johann Bode in
1871. The " law " later failed in the cases of the outermost
planets Neptune and Pluto, but it was flawed from the outset with
respect to distances of both MERCURY and EARTH, as Titius was perhaps
aware.
NEXT
III The Exponential
Order
http://www.spirasolaris.ca/sbb4c_07.html
The constant of linearity for the resulting planetary framework
is the
ubiquitous constant Phi known since antiquity. Major departures
from the theoretical norm are the ASTEROID BELT, NEPTUNE, and EARTH in
a resonant synodic position between VENUS and MARS.
Fibonacci/Golden Section Resonances in the Solar System.
Return to Spira Solaris