Spira Solaris Archytas-Mirabilis Part IV
[ EXCERPT] PART IVD2C: THE PHEIDIAN PLANORBIDAE

A. TO ORDER ALL THINGS NOT ORDERED
A.1 THE PHEIDIAN PLANORBIDAE
The present paper is a continuation of the investigation begun in previous sections concerning the spiral form in Nature, Time, and Place. Here, although more ancient roots undoubtedly exist the emphasis is now concentrated primarily on the past three centuries--roughly from the time of Carl Linnaeus (1707-1778) onward. But it is not an historical analysis per se, nor is it a commentary on the momentous changes that took place during this tortuous period. At least not directly, though a darker, negative side of the matter also surfaces as the investigation proceeds. This development itself is perhaps surprising since it is linked to a specialized yet apparently innocuous topic, namely the spiral formations evident in ammonites and shells. On the other hand, however, it is not quite so surprising, or entirely unexpected when the dynamics of the matter become apparent. 
    Nevertheless, on a more positive note the present study was precipitated somewhat fortuitously by the format adopted by Simon Winchester for his recent best-selling work:The Map that Changed the World: William Smith and the Birth of Modern Geology (2001). The format followed in this publication was explained by the latter as follows:1

CHAPTER-OPENING ILLUSTRATIONS
Incorporated in eighteen of the nineteen chapter openings (including those of the prologue and the epilogue) will be found small line drawings of Jurassic ammonites, long-extinct marine animals that were so named because their coiled and chambered shells resembled nothing so much as the horns of the ancient Egyptian ram-god, Ammon. Soun Vannithone's drawings of these eighteen specimens are placed in the book in what I believe to be the ammonites' exact chronological sequence. This means that the book's first fossil, Psiloceras planorbis, which illustrates the prologue, is the oldest ammonite, and is to be found deepest down in any sequence of Jurassic sediments; by the same token the final fossil, Pavlovia pallasioides, comes from a much higher horizon, and is very much younger. Much like the epilogue it illustrates, it was fashioned last. It must be said, though, that anyone who flips rapidly from chapter to chapter in the hope of seeing a speeded-up version of the evolutionary advancement of the ammonite will be disappointed: Ammonites floating, pulsating, slow-swimming beasts that were hugely abundant in thc warm blue Jurassic seas do not display any conveniently obvious changes in their Idealures, they neither become progressively smaller with time, nor do they become larger; their shells do not become more complex, or less. True, some ammonites with very ridged shells do indeed evolve into smoother-shelled species over the ages, but these same creatures then become rougher and more ridged again as time wears on, managing thereby to confuse and fascinate all who study them. Only studies of ammonites from successive levels will reveal sure evidence of evolutionary change, and such study is too time consuming for the chance observer. Ammonites are, however, uniformly lovely; and they inspired William Smith: two reasons good enough, perhaps, for including them as symbols both of Smith's remarkable prescience and geological time's amazing bounty. However: eighteen ammonites and nineteen chapter openings? There is one additional illustration, of the microscopic cross-section of a typical oolitic limestone, which I have used to mark the heading for chapter 11. Since this chapter is very different in structure from all the others, and since much of its narrative takes place along the outcrop of those exquisitely lovely, honeycolored Jurassic rocks known in England as the Great Oolite and the Inferior Oolite, it seemed appropriate and reasonable to ask the legions of ammonites, on just this one occasion, to step or swim very slowly to one side.
Prologue: Psiloceras planorbis.... (Simon Winchester, The Map that Changed the World, Harper Collins, New York, 2001: ix-x)

A fascinating set of "Pheidian" spirals it would seem, and all carefully laid out in planview in addition. Then there was the line of development sketched out to feed curiosity even further--Ammon, Rams, Ramshorn Snails, Ammonites. Yes, of course! ...but planorbis? A strange name, but plentifully applied it would seem, and not only among ammonites either, but ramshorn snails and the like going back to at least the time of Linneaus (1758). And also thereafter into and beyond the early part of the Nineteenth Century, especially Say in the former period. As for the beautiful line drawings at the beginning of each chapter of The Map that Changed the World, they were that indeed, and although most were tighter spirals than Spira Solaris per se, they were nevertheless recognizable as equiangular spirals lying within the range already formulated and plotted in astronomical contexts, i.e., from the inverse velocity spiral Phi 1/3 to the planetary period spiral, Phi 2.

Figure 1. The Growth factor for Spira Solaris

Figure 1. Spira Solaris, Growth factor k = Phi 2
For more on this spiral and the Capacious Manitoba Ramshorn snail see Figure 13 {omitted here}

Thus further Pheidian spirals with growth factors between 1.1739850 and 2.61803398874 : 1, five of which had already been generated--two for the Periods, two for the Distances and one for the inverse Velocity. Up to this point, however, the emphasis had remained with the equiangular spiral based on Phi 2 in view of its all-inclusive nature on one hand and the confusion four additional spirals might have occasioned on the other. Now there was a practical reason for widening the range, though remnants of the earliest ammonite, Psiloceras planorbis provided insufficient definition to determine the fundamental spiral, at least with any degree of certainty. This said, however, it was still apparent that while the associated spiral in this instance was not Spira Solaris, it was nevertheless possibly related, for the Distance equivalent (i.e., the equiangular spiral k = Phi 4/3 with a growth factor of 1.899547627 : 1) did in fact provide a limited fit. Enough of an association, in fact, to give impetus to a more detailed investigation--one that was to have a number of unexpected results.

A.2. THE PLANORBIDAE: FORMS
Although the assignment of the equiangular spiral k = Phi 4/3 to Psiloceras planorbis remains uncertain, the naming and classification of various "planorbidae" through the Eighteenth, Nineteenth and Twentieth Centuries--especially with respect to snails--opened up a fascinating and potentially useful line of inquiry. The first order of business here was obviously to conduct a survey to determine whether or not the "planorbidae" were indeed Pheidian in the sense stated in the previous section ("equiangular spirals based on the constant Phi raised to any power, whether integer, fractional part or any number whatsoever") and secondly, to establish whether or not the latter possessed the suspected relationship to Spira Solaris and associated spirals. For this purpose the range covered by the original five spirals mentioned earlier was extended to include further exponential "thirds" and "sixths." The former (in the simplest sense) being the natural continuation of the above mentioned range k = Phi 1/3 through k = Phi 6/3 with the insertion of the "missing" spiral k = Phi 5/3 between Phi 4/3and Phi 2; followed by the inclusion of k = Phi 7/3,  k = Phi 8/3 and finally, k = Phi 9/3 for a provisional upper limit. Next, the intermediate "sixths" were inserted to provide a test range that extended from k = Phi 1/6 to k = Phi 18/6 (growth factors 1.08450588 to 4.236067978) resulting in some 18 pheidian spirals--likely more than sufficient for ammonites, though clearly inadequate for all shells.

   Here it should be emphasized that this preliminary range was neither haphazardly nor arbitrarily determined. It was in fact specifically predetermined by what might best be called the test dynamics of the matter, with emphasis not only on the original five Spira Solarii, but also on the "thirds" on either side of Spira Solaris and possibly beyond. The rationale behind this selection will become apparent later; as it was, for spirals where the growth constant k was larger than unity standard computations involving six revolutions with 360 data points per revolution were employed--thus 6 complete cycles with a total of 2160 data points for each equiangular spiral. Where the growth constant k was less than unity additional cycles were added as the growth factors diminished. Nevertheless, the preparation of the test set was hardly a difficult task--the basic  mathematical elements have long been known, e.g., as described in detail by Sir D'Arcy Wentworth Thompson2 (On Growth and Form, 1917,1942, 1966 and 1992); by H.E. Huntley 3 (The Divine Proportion, 1970--my own introduction to the topic), by Jay Kappraff 4 (Connections, 1991) and for spreadsheet users, the PHB Practical Handbook of Spreadsheet Curves and Geometric Construction (1993) by Deane Arganbright.5 For the present analysis, however, each spiral was further expanded to include two intimately related forms locked in position and scale with respect to each other. As will be explained later, these double forms were rigidly determined from a fixed mathematical relationship. Thus, for example, the single equiangular spirals for the "Spiral of Pheidias" (Schooling 1914) and Spira Solaris were each joined by their respective additional pairs to form associated triple sets as shown below, thus raising the original test set to 54 pheidian spirals with more likely to be generated on an as-required basis.

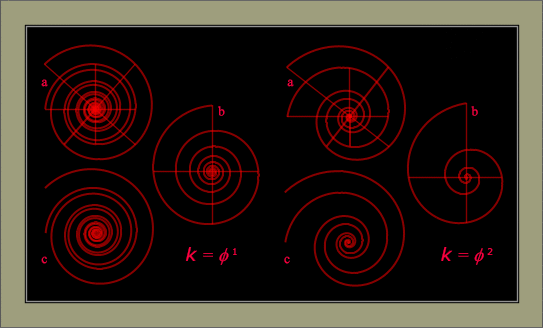
Fig. 1a The Triple spiral configurations for Pheidas and Spira Solaris

Figure 1a. Triple spiral configurations for Pheidas (left) and Spira Solaris (right)

In the above, b represents the standard format, a and c the dual additions--the latter configuration identical to the former, but without the cross-reference lines. Both the origin and the technical details of these dual configurations will be supplied later, but in passing the extended forms may appear vaguely familiar to some readers, especially those acquainted with Sir Theodore Andrea Cook's The Curves of Life (1914:64, 278) 6 and Samuel Colman's Nature's Harmonic Unity (1911:115) 7. As for their application in the present survey, their occurrence was a continual series of surprises, for both dual formats seem to be apparent in certain classifications, i.e., form a appears to be a prominent feature among the more elongated Halitodae, while c is also evident among certain shells with smaller growth factors, the Spiral of Pheidias included. One other point of interest (though not pursued further here) is the change evident in c for the increase in growth factor between Phi and Phi 2. For the curious, the "natural" changes in form that accompany higher powers of Phi in this configuration also provide further room for thought, as shown below:

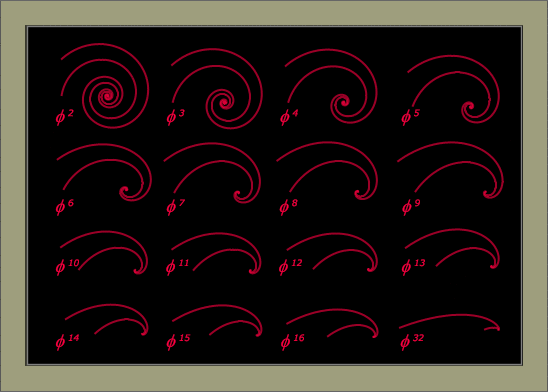
Figure 1b. Dual spiral configurations

Figure 1b. Dual Pheidian configurations:  k = Phi 2 to k = Phi 16 plus k = Phi 32

For the initial survey the pheidian thirds and sixths were applied in a standard manner, and apart from uniform scaling and rotation as required, the test spirals remained unmodified throughout. Lastly, the generated data were converted to standard graphical formats, rendered translucent to aid scaling and fitting, and then passed to a suitable platform for the testing phase. The software of choice here was XARA-X, which, as it turned out, was also capable of producing the output graphics and associated figures.
   Before describing the latter a few words concerning the initial testing phase and anticipated difficulties are perhaps in order. It was realized from the start that it is one thing to attempt to fit a two-dimensional spiral to drawings of three-dimensional objects, and yet another to attempt the same procedure with photographs, which may or may not have been influenced by perspective effects; optical systems, focal lengths, depths of field, and also quite possibly artistic licence. Some part, all, or none of which might also get carried over to line drawings. Then there were the many problems arising from natural growth itself to be taken into consideration, with no truly perfect spiral expected to be encountered and minor departures anticipated in certain cases. Fortunately, many ammonites possess relatively simple symmetrical forms, i.e., spiral growth largely confined to two dimensions without spires or appendages extending away from the primary spiral (e.g., Figures 1e, 1b2, 1c, and 1d-1d3 below). 
   Nevertheless, the investigation--even for the relatively flat and largely symmetrical ammonites--began with no great expectations, but happily with a wealth of available material. And, as it turned out, Soun Vannithone's accurate plan-view line drawings provided both an ideal starting point and an excellent training ground; witness:

Ammonites and the Pheidian Planorbidae

Fig. 1e. Ammonites 69 and the Pheidian Planorbidae ( k = Phi  5/6 )

 I will not go further into the ammonite phase of the testing here except to say that overall (in spite of the complexity of the matter and the variations encountered) the initial ammonite survey provided sufficient information to yield positive answers to both the first and second questions posed. Namely, that the spiral configurations examined could indeed be considered in pheidian terms, and secondly, that the examples tested were also sufficiently relatable to the Pheidian sixths and thirds associated with Spira Solaris to merit the title Pheidian planorbidae, e.g., Figure 1b2,  k = 6/3 = Phi 2 (c: single, and b: dual Spira Solaris ),61 Figure 1C: k = Phi  to the 3/3,  4/3,  5/3,  6/3 powers respectively (five ammonites from: Ammonites et autres spirales by Hervé Châtelier 61-65) and Figure 1d: k = Phi to the 3/3 power (The Spiral of Pheidias), ammonite from Lower Jurassic Ammonites by Christopher M. Pamplin.66  Figure 1d2: k = Phi  4/3 and Figure 1d3: k = Phi  5/3 are from Jurassic ammonites and fossil brachiopoda 67  by Jean-ours and Rosemarie Filippi 67.

Figure 1b2. Ammonites and the Dual Pheidian configuration

Figure 1b2. Ammonitesr 61 and the Dual Pheidian configuration ( k = Phi 2)

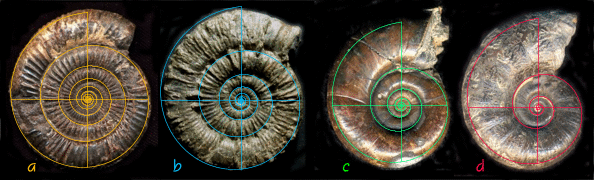
Figure 1c. Ammonites and Fig. 1c. Ammonites and the Pheidian Planorbiae I

Figure 1c. Ammonites 62-65 and the Pheidian Planorbidae I ( k = Phi,  Phi 4/3,  Phi 5/3 and  Phi 2 ):
 

Figure 1d.

Figure 1d. Ammonites 66 and the Pheidian Planorbidae II (k = Phi)

valdimax1.gif

  Fig. 1d2. Ammonites 67 and the Pheidian Planorbidae III ( k = Phi 4/3)

Ammonites and the Phedian Planorbidae IIv

 Fig. 1d3. Ammonites 68 and the Pheidian Planorbidae IV ( k = Phi 5/3)

Thus the Phedian Planorbidae as applied to ammonites from an initial survey--one small inroad into a complex subject with accompanying dynamic, temporal and historical overtones that all appeared to merit further examination.
   Next--based on the positive indicators gained from the ammonite phase the testing moved on to "planorbid" snails, the treatment of which will also be deferred until later--not because of its simplicity, but the exact opposite--its undoubted complexity (see Figure 13 below).
   Finally, from these two bases the survey naturally turned to the more varied and extensive range of spirals found among seashells.


A.3. PHEIDIAN PLANORBIDAE APPLIED TO SHELLS  I
Part of the third phase of the testing is shown below in Figure 2. Although the selection includes some better known shells, it also omits others--primarily to emphasize certain points in each of the selected cases.To maximise relevant information the examples are also shown against a background plot of pheidian growth factors along the y-axis with the corresponding equiangles of the associated pheidian spirals along the x-axis for the successive exponential thirds from 1 through 9. For the study (following Mosely 1838) 8 the growth factor itself was taken to represent the "characteristic number" (n) of the associated "primary" spiral which was also the parameter k.
    Here the reader should be aware that little of what is presented below is new per se, nor is it presented as such here. Many of the assignments, although neglected at present, were obviously known in earlier times to one degree of accuracy or another, as the tables of related data for shells in Thompson's On Growth and Form (1917) clearly attest 9, e.g., the values determined by Nauman (1848, 1849),10 Muller (1850,1853)11and Macalister (1870)12.
    As for the primary spiral assignments for the nine shells shown in Figure 2, they proceed in due order from the lowest pheidian planorbidae (k = Phi 1/3) to the largest of this group, k = Phi 9/3.
Briefly, the assignments are as follows:
The above represent a small selection from the test survey. Although far from inclusive, the range for the shell phase of the survey extended from the tighest spiral (k = Phi 1/12; n = 1.040915886) out to Anadara brasiliana (Arc), k = Phi 10 (n = 122.991869381). Other shells tested included Terebra, k = Phi 1/6 (n = 1.083505882); Acropora, k = Phi 1/3 (n = 1.173984997);Turritella duplicata, (after Mosely, k = Phi 1/3; n = 1.173984997); Trochus (varied), k = Phi 1 (n = 1.618033989) and also one or two of the better known shells, e.g., Thatcheria Mirablis, k = Phi 7/6 (n = 1.753149344). There were additional assignments, but to "concatenate without abruption" (as Dr. Johnson was want to put it) would likely disrupt the general thrust of the paper, which is not the assignment of pheidian spiral forms to shells per se, but the dynamic, historical, and general implications. Moreover, in so much as a full description of the various assignments shown here should rightly follow after the dynamics of the matter are introduced the following descriptions are limited to a few notes concerning some of the major points of interest. Similarly, discussion of the Haliotidae (Abalone; excellent test subjects because of their generally flat shapes and well-defined open spiral forms) is also deferred until later in view of the possible relationship between this type of shell and the complexities inherent in phi-related "whirling rectangles" (esp. Haliotis parva; k = Phi 4 ; see A4 below).

Figure 2. Phedian Planobidae I

Fig. 2 The Pheidian Planorbidae. Thirds: Growth Factors/Expansion Rates 1.174 to 4.236


[ COMMENTS AND ADDITIONAL GRAPHICS FOR FIGURES 2A AND 2B OMITTED ]

Figure 2C. Architectonica perspectiva (Linnaeus 1758) and Similar Shells
Figure 2C is shown in inverted planview for two major reasons. Firstly, a trio of like shells graced the dust cover of the 1942 edition of Sir D'Arcy Wentworth's On Growth and Form in this exact representation. The reason seems clear enough from the inverted "perspective" of the associated spiral (see Figure 5 below; perhaps the latter was also influenced by Aristotle, if not the three-fold number--"Said Aristotle, prince of philosophers and never-failing friend of truth: All things are three"). Here, one should also note that the "ratio of breadth of consecutive whorls" in Thompson's tabular data for shells of this general type, i.e., Solarium trochleare is given as 1.62 25, thus the Golden Section to two decimal places. The degree of accuracy is low, but hardly conclusive proof that a better value was not known. In fact there is very good reason (as explained in detail below) to believe that both Canon Mosely and Sir D'Arcy Wenthworth Thompson were intimately acquainted with the not only the Phedian planorbidae per se, but also the dynamics of the matter.
In the meantime, Figure 5 below emphasizes not only the distinct markings and underside perspective view, but also the fit in standard and open double form with respect to the top markings of the shell.

Fig.5 Architectonica perspectiva

Fig.5. The underside and top of Architectonica perspectiva;
Single spiral (B and C); open double spiral (A); each k = Phi 1


[ COMMENTS AND INDIVIDUAL GRAPHICS FOR FIGURES 2D-2I AND ADDITIONAL SHELLS OMITTED ]

[ BIBLIOGRAPHY BELOW.  REMAINING SECTIONS OF SBB4D2, THE "DYNAMICS" OF THE MATTER, AND THE APPENDIX OMITTED ]

REFERENCES

  1. Winchester, Simon. The Map that Changed the World, Harper Collins, New York 2001.
  2. Thomson, Sir D'Arcy Wentworth. On Growth and Form, Cambridge University Press, Cambridge 1942; Dover Books, Minneola 1992.
  3. Huntley, H. E. The Divine Proportion: A Study of Mathematical Beauty, Dover, New York 1970.
  4. Kappraff, Jay. Connections:The Geometric Bridge Between Art and Science, McGraw-Hill, New York 1991.
  5. Arganbright, Deane. PHB Practical Handbook of Spreadsheet Curves and Geometric Construction, CRC Press, Boca Raton 1993.
  6. Cook, Sir Theodore Andrea. The Curves of Life, Dover, New York 1978; republication of the London (1914) edition.
  7. Colman, Samuel. Nature's Harmonic Unity, Benjamin Blom, New York 1971.
  8. Mosely, Rev. H. "On the geometrical forms of turbinated and discoid shells," Phil. trans. Pt. 1. 1838:351-370.
  9. Thomson, Sir D'Arcy Wentworth. On Growth and Form, Cambridge University Press, Cambridge 1942; Dover Books, Minneola 1992. 
  10. Nauman, C.F. "Ueber die Spiralen von Conchylieu," Abh. k. sachs. Ges. 1846; "Ueber die cyclocentrische Conchospirale u. uber das Windungsgetz von Planorbis corneus," ibid. I, 1849:171-195; "Spirale von Nautilus u. Ammonites galeatus, Ber. k. sachs. Ges. II, 1848:26; Spirale von Amm. Ramsaueri, ibid. XVI, 1864:21.
  11. Muller, J. "Beitrag zur Konchyliometrie," Poggend. Ann. LXXXVI, 1850:533; ibid. XC 1853:323.
  12. Macalister, A. "Observations on the mode of growth of discoid and turbinated shells," Proc. R.S. XVIII, 1870:529-532.
  13. Telescopium telescopium Linneaus 1758. Source: S. Peter Dance, Shells and Shell Collecting, Hamlyn Publishing Group, London 1972:32.
  14. Conus princeps f. lineolatus Valenciennes1832. Source: G. Paganelli,  Conus princeps f. lineolatus 1197. coneshell.net
  15. Architectonica perspectiva Linneaus 1758. Source: S. Peter Dance, Shells and Shell Collecting, Hamlyn Publishing Group, London 1972:52-53.
  16. Harpa kajiyamai Rehder 1973.Source: Machiko Yamada, (Defunct link: http://www.bigai.ne.jp/pic_book/data20/r001967.html)
  17. Pedinogyra hayii Griffith & Pidgeon 1833 (Hay's Flat-whorled Snail). Source: Machiko Yamada  (Defunct link: http://www.bigai.ne.jp/pic_book/data20/r001967.html)
  18. Planorbis corneus, Linnaeus 1758; Source: Martin Kohl, (Defunct link: http://members.aol.com/Mkohl1/Pulmonata.html)
  19. Nautilus pompilus, Linnaeus 1758. Source: SEASHELLS. World of Nature Series, W.H. Smith, New York.
  20. Haliotis brazieri, Angas 1869. Source: D. L. Beechey, Haliotis brazieri; Index: Shells of New South Wales.  20a. Haliotis brazieri (smooth form variant)
  21. Haliotis scalaris, Leach 1814, Source: Machiko Yamada, (Defunct link: http://www.bigai.ne.jp/pic_book/data20/r001967.html)
  22. Thompson, Sir D'Arcy Wentworth. On Growth and Form, 1992:
  23. Conus mercator, Linnaeus 1758 and Conus ammiralis f. hereditarius DA MOTTA, 1987. Source: G. Paganelli, coneshell.net
  24. Conus tulipa, Linnaeus 1758. Source: G. Paganelli, Conus tulipa 710, coneshell.net
  25. Thompson, Sir D'Arcy Wentworth. On Growth and Form, 1992:816.
  26. Harpa goodwini. Source: Guido T. Poppe, Conchology (Defunct link: http://www.conchology.uunethost.be/ )
  27. Clarke, Arthur H.The Freshwater Molluscs of Canada, National Museum of Natural Sciences, Ottawa 1981. 
  28. ibid., p.175.
  29. Kohl, Martin. Freshwater Molluscan Shells: Planorbidae (Defunct link: http://members.aol.com/mkohl2/Planorbidae.html)
  30. Ovid, as quoted by Nicole Oresme in Du Ciel et du monde, Book II, Chapter 25, fols. 144a-144b, p.537.
  31. Liguus virgineus Linnaeus, 1758. Source: Harry Lee, jaxshells.org: http://www.jaxshells.org/ligver.htm  Index: http://www.jaxshells.org/
  32. Helisoma pilsbryi infracarinatum (Great Carinate Ramshorn Snail, Baker 1932). Source: Arthur H. Clarke.The Freshwater Molluscs of Canada, National Museum of Natural Sciences, Ottawa 1981:210.
  33. Helisoma (pierosoma) corpulentum corpulentum (Capacious Manitoba Ramshorn Snail , Say 1824). Source: Arthur H. Clarke. The Freshwater Molluscs of Canada, Ottawa 1981:206.
  34. Promenetus exacuous megas ( Broad Promenetus Dall, 1905. Source: Arthur H. Clarke.The Freshwater Molluscs of Canada, National Museum of Natural Sciences, Ottawa 1981:189.
  35. Thompson, Sir D'Arcy Wentworth, On Growth and Form, 1992:751-753.
  36. Hambidge, Jay. Dynamic Symmetry, Yale University Press, New Haven 1920:16-18.
  37. Kappraff, Jay. Connections:The Geometric Bridge Between Art and Science, McGraw-Hill, New York 1991:46. 
  38. Thompson, Sir D'Arcy Wentworth, On Growth and Form, 1992:791. 
  39. Haliotis parva,  Linnaeus 1758. Source: Molluscs.net: Haliotis parva; Index: http://www.molluscs.net/
  40. Harris, John N. "Projectiles, Parabolas, and Velocity Expansions of the Laws of Planetary Motion," JRASC, Vol 83, No. 3, June 1989:207-218.
  41. Wagner, Jeffrey K. Introduction to the Solar System, Holt, Rinehart & Winston, Orlando 1991:426.
  42. Marine decorated rhyton from Zakros (Crete). Wondrous Realms of the Aegean, selected by the editors, Lost Civilizations Series, Time-Life Books, Virginia 1993:110.
  43. Embossed, carved 12-inch rhyton from Zakros (Crete). Wondrous Realms of the Aegean, selected by the editors, Lost Civilizations Series, Time-Life Books, Virginia 1993:99.
  44. Bretagnon, Pierre and Jean-Louis Simon, Planetary Programs and Tables from -4000 to +2800, Willman-Bell, Inc. Richmond, 1986.
  45. Pierce, Benjamin. "Mathematical Investigations of the Fractions Which Occur in Phyllotaxis," Proceedings, AAAS, II 1850:444-447.
  46. Agassiz, Louis. Essay On Classification,  Ed. E. Lurie, Belknap Press, Cambridge 1962:127-128.
  47. Harris, John N. "Projectiles, Parabolas, and Velocity Expansions of the Laws of Planetary Motion, " JRASC, Vol 83, No. 3, June 1989:216.
  48. Raup, David. "Computer as aid in describing form in gastropod shells," Science 138, 1962:150-152. 
  49. Phillips, Tony and Stony Brook, "The Mathematical Study of Mollusk Shells" American Mathematical Society; AMS.ORG. 
  50. Thompson, Sir D'Arcy Wentworth. On Growth and Form, Cambridge University Press, Cambridge 1942; the complete unabridged reprint, Dover Books, Minneola 1992.
  51. Turritella duplicata, Source: Canon Mosely, in  Sir D'Arcy Wentworth Thompson, On Growth and Form, the complete unabridged edition, 1992:772.
  52. Euhoplites truncatus (Spath 1925). Source: Jim Craig: Euhoplites truncatus. Index: Fossils of the Gault Clay and Folkestone Beds of Kent, UK
  53. Dawkins, Richard. Climbing Mount Improbable, W.W. Norton, New York 1996:198:223. 
  54. _____________  Aruneus diademus Spider.Climbing Mount Improbable, Norton, New York 1996:58. 
  55. On Growth and Form, 1942:784. 
  56. On Growth and Form, 1942:773. 
  57. Lurie, E. (Ed.) Essay On Classification,  Belknap Press, Cambridge 1962:128.
  58. Church, Arthur Harry. On The Relation of Phyllotaxis to Mechanical Law, Williams and Norgate, London 1904; see also: http://www.sacredscience.com (cat #154).
  59. Colman, Samuel. Nature's Harmonic Unity, Benjamin Blom, New York 1971:3.
  60. Thatcheria mirabilis (Angas 1877). Source: Mathew Ward, Photographer; in Peter S. Dance, Shells, Stoddart, Toronto 1992.
  61.  Hildoceras bifrons, (Bruguière 1789).  Figure 1b2. Source: Hervé Châtelier, Ammonites et autres spirales - Hervé Châtelier.
  62. Dactylioceras commune (Sowerby 1815).  Figure 1Ca. Source: Hervé Châtelier, Ammonites et autres spirales.
  63. Porpoceras vortex (Simpson 1855).  Figure 1Cb.  Source: Hervé Châtelier, Ammonites et autres spirales.
  64. Protetragonites oblique-strangulatus (Kilian 1888).  Figure 1Cc. Source: Hervé Châtelier, Ammonites et autres spirales.
  65. Lytoceras cornucopia (Young & Bird 1822).  Figure 1Cd.  Source: Hervé Châtelier, Ammonites et autres spirales.
  66. Epophioceras sp. (Spath, 1923). Figure 1D. Source: Christopher M. Pamplin, (Defunct link: Lower Jurassic Ammonites. http://ammonites.port5.com/epop.htm)
  67. Acanthopleuroceras valdani (D'Orbigny). Figure1d2. Source: Jean-ours and Rosemarie Filippi: Jurassic ammonites and fossil brachiopoda.
  68. Aegoceras (Aegoceras) capricornus (Schlotheim). Figure 1d3:  Source: Jean-ours and Rosemarie Filippi: Jurassic ammonites and fossil brachiopoda.
  69. Ethioceras raricostatum (Figure 1e). Line drawing by Soun Vannithone, in Winchester, Simon. The Map that Changed the World, Harper Collins, New York 2001:1
  For U.K. Ammonites, see:  FOSSILS OF THE GAULT CLAY AND FOLKESTONE BED OF KENT, UK  by the late Jim Craig, and  FOSSILS OF THE LONDON CLAY  by Fred Clouter.

Copyright © 2002. John N. Harris, M.A.(CMNS). Last updated on April 2, 2009.
Ammonite graphics (Figures 1b2, 1c and 1d) added on April 29, 2003; Figure 21c on June 4 2003; Figure. 7b added 11 May, 2004; Figures 22a, 22b, and 1d3 added 17 July, 2004. Figures1 and 1e on 18 July, 2004.

Return to Spira Solaris

PREVIOUS SECTION

NEXT SECTION