PART I. BODE'S FLAW
More correctly
called the Titius-Bode relationship, the ad hoc scheme to
account
for the mean distances of the planets from the Sun known as "Bode's
Law"
was originally conceived by Johann Titius in 1766 and then relegated by
the latter (perhaps because of its deficiencies) to the status of a
page-note.
Subsequently revived and popularized by Johannes Bode in 1772, the
"Law"
correlated well enough with the mean distance of the newly discovered
major
planet Uranus (1781) and also that of the largest asteroid Ceres
(discovered
in 1801), but it later failed completely when applied to the mean
distances
of Neptune and Pluto. Nevertheless, apart from latter-day variants1-7 of
Bode's Law it would seem that the underlying structure of the Solar
System
still remains essentially undetermined. Yet there are obvious
objections
to Bode's Law over and above its ad hoc nature and the fact
that
it is no law all. In reality, the scheme was a dubious combination of two
separate ad hoc relationships that was flawed from the outset,
as
Titius himself was perhaps aware. In particular, with reference to unity
and the ad hoc constants:
A = 4, B = 3,
C
= 10, the first part of the "Law" applies only to the mean
heliocentric
distance of Mercury, the first planet from the Sun, i.e.,
whereas the rest of the
mean distances are obtained from the application
of a second ad hoc relationship expressed in terms of
exponents
as follows:
Relation [2] either
begins with the mean distance of Venus
for
n
= 0, or requires the ultimate limit of minus infinity
to commence with the mean distance of Mercury, as Nieto5 and others
have noted. For exponents 0
through 5 the second relationship nevertheless approximated
the mean distances of five of the six planets then known, and also
suggested
(albeit for no good reason), that a planetary position might
exist
between Mars and Jupiter. It is true that the largest asteroid Ceres
was
subsequently found near the position in question, but even so this
relatively
minuscule object hardly possesses suffficent mass to qualify as a
planet
per
se. Actually, relation
[2] is quite misleading, especially with
respect to the apparent doubling associated with the component 
. In this relation planet-to-planet increases in
distance undoubtedly
approach a limiting value of 2 as n
becomes
large, but only at the expense of the ad hoc parameter
A, which becomes increasingly less significant. A plot of
the increase in
mean distances between adjacent planets (Figure 1) also
emphasizes
that even before the discoveries of Neptune and Pluto that Bode's Law
was
no smoothly increasing function, with or without Ceres.
More specifically, the ratio
of the increase in distance between Mercury and Venus is 1 : 1.75
, but instead of being greater, the ratios for the next two
planetary positions (Venus : Earth and Earth : Mars
respectively) are in fact lower, i.e., 1 : 1.42857
and 1 : 1.6 respectively. Moreover, the situation is
actually
worse with respect to the mean distances of the Solar System itself.
Beyond
Mars the Bode's Law ratios rise to 1.75 again, and
thereafter
they increase steadily towards the limiting value. But even so, the
actual
distances and the ratios for the Solar System diverge radically from
Bode's
Law beyond Uranus, as Figure 1 shows. Thus although relation [2]
at first glance appears to represent a reasonable sequential expansion,
it is far from that, and perhaps more the result of judicious ad hoc
adjustments than anything else. As a result, there is a contrived 1
: 1 correlation between the "law" and the Solar System with
respect
to the mean distance of Earth. On examination, however, it turns out
that
this position actually possesses one of the poorest correlations of all
with respect to the planet-to-planet increases.
Thus there is not only a definite
kink in the "law," there is also a major question mark concerning the
position
of Earth itself. In fact, it appears that the ratios and the resulting
distances for Earth and Mars are both atypical, those
pertaining
to Earth especially so. The "law" implies that planet-to-planet
distances
increase exponentially towards a ratio of 2 : 1, but in
the
case of the Venus-Earth increase it is closer to the square root of
two, or, in general astronomical terms, Earth's position appears to
correspond more to the synodic difference cycle between Mars
and
Venus than a planetary position per se.
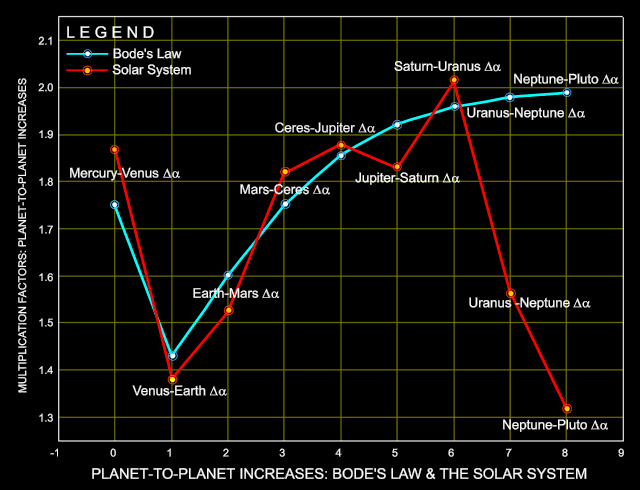
Figure 1. The Kink in Bode's Law
But what are the norms for
planetary systems in any case, and where might the Solar System fit in
the general scheme of things? We now know that this planetary system
embodies
a number of anomalies, including major variations in planetary
composition
and size, exceptions in both orbital and rotational inclination, marked
differences in eccentricity, an asteroid belt of debatable origin,
as-yet
unexplained periodic changes in solar output, planetary resonances, and
that the System is also subject to chaotic orbital behaviour. Moreover,
although it is generally accepted that the Sun and planets owe their
origins
to the process of accretion, there still remains an apparent lack of
primordial
residue, an unusual mass/momentum distribution between the Sun and
planets,
and a slower than expected solar rotational speed to be factored into
the
equation. Because of these anomalies it would seem unlikely that the
Solar
System is perfect, unchanging, and readily represented by ordinal
numbers
and simple expansions, etc. In fact, recent chaos theory-related
investigations
carried out by Sussman,8
Wisdom,9
Kerr,10-11
Milani,12 Laskar et
al,13-16
and
others have now established that the Solar System can no longer be
considered
to be immutable or stable in perpetuity.
Thus the situation is not only
as described by Ivars Petersen17
in his 1993 publication: Newton's Clock: Chaos in the Solar System,
it also appears--as Heraclitus generalized it so very long ago--that
"all
things flow and nothing stands." Because of these considerations it
therefore
makes very little sense to base any detailed analysis of the structure
of the Solar System on ad hoc functions, especially those that
are
neither continuous nor sequential in the first place.
How then should we proceed?
And what are the viable alternatives? These questions and partial
answers
provide the subject matter for Part Two.
III The Exponential
Order
http://www.spirasolaris.ca/sbb4c_07.html
The constant of linearity for the resulting planetary framework
is the
ubiquitous constant Phi known since antiquity. Major departures
from the theoretical norm are the ASTEROID BELT, NEPTUNE, and EARTH in
a resonant synodic position between VENUS and MARS.
Fibonacci/Golden Section Resonances in the Solar System.