Times Series Analysis gif

INTRODUCTION

The advent of modern computing devices and their application to time-series analyses permits the investigation of mathematical and astronomical relationships on an unprecedented scale. Moreover, since neither numerical complexity nor calculation intensity now pose insuperable difficulties, it becomes feasible to treat single events sequentially and apply detailed time-series analyses to the results to any required degree.The following discussion primarily concerns the real-time heliocentric motions of the four major superior planets (Jupiter, Saturn, Uranus and Neptune) and four terrestrial planets (Mercury, Venus, Earth and Mars), plus their various interactions. Shown in graphical form in the second section, the final outputs were based initially on the single-event formulas provided by Bretagnon and Simon (1986) adapted to produce time-series data utilising spreadsheet methodology (Lotus 1-2-3), which proved particulary well suited to the task. To each their own ...

PLANETARY MOTION, SINGLE-EVENT AND TIME SERIES FORMULAS

A. THE MAJOR SUPERIOR PLANETS
The methodology and formulas applied to planetary motion in this context are provided by Pierre Bretagnon and Jean-Louis Simon in Planetary Programs and Tables from - 4000 to +2800 (Willman-Bell, Richmond, 1986). The astronomical programs in this work concern the determination of the positions of the planets as viewed from Earth (i.e., geocentric coordinates with corrections for aberration, nutation, and precession, etc). The first stage, however, concerns the determination of heliocentric coordinates. For Jupiter, Saturn, Uranus and Neptune the latter are obtained from the following power series formulas:

HELIOCENTRIC LONGITUDE (L)

HELIOCENTRIC LATITUDE (B)

HELIOCENTRIC RADIUS VECTOR (R)

The parameter V is measured in units of 2000 julian days from the beginning of successive five-year intervals; the units are radians for L and B, and astronomical units ( AU ) for R. Tables for the motion of Jupiter, Saturn, Uranus and Neptune are obtained from power series data for five-year intervals, e.g., for the period 1990 to 1995 BP starting with Julian Day 2447892.5 the tables are as follows [Bretagnon and Simon 1986:124, 140]:

JUPITER 1990 2447892.5 

L) 1.678682 2.956725 -0.414596  0.004826 0.299734 -0.151349  0.029332
B)-0.005204 0.067083 -0.000759 -0.109760 0.078191 -0.029462  0.007110
R) 5.155577 0.717884  0.187303 -1.133334 0.310164  0.141854 -0.042529

SATURN 1990 2447892.5 
L) 4.993758 1.054503  0.014505 0.023160 -0.000553 -0.000863 -0.000059
B) 0.005629-0.045382 -0.003796 0.007466  0.000345  0.000362 -0.000177
R)10.027146-0.144092 -0.300680 0.032117  0.003847  0.022473 -0.008193

URANUS 1990 2447892.5 
L) 4.808885 0.401780 -0.007396 0.001186 -0.000138 -0.000220  0.000115
B)-0.004951-0.000503  0.000528-0.000054  0.000306 -0.000299  0.000108
R)19.380045 0.357595 -0.005398-0.008060 -0.013812  0.011760 -0.004261

NEPTUNE 1990 2447892.5 
L) 4.923200 0.207762  0.000166 0.000853 -0.000671  0.000373 -0.000118
B) 0.015270-0.005562 -0.000339 0.000013  0.000032 -0.000016  0.000004
R)30.210400-0.047301  0.013832 0.001610 -0.018511  0.014834 -0.005138
The first line gives the year of the beginning of the time-span and the julian date (January 1) at 0h ET. The second line gives the seven coefficients of the polynomial for the heliocentric longitude L, the third the coefficients for the heliocentric latitude B and the forth the coefficients for the heliocentric radius vector R.

TIME
Ephemeris Time (ET); the variable V(t) obtained from the following relation:

 

where T0 is the beginning julian date of the time-span, T i is the required point in time for the superior planet (s) in question and V ranges from 0 to 0.915.

REAL-TIME PLANETARY ORBITS
Plan-view plots of planetary orbits require the computation of the heliocentric longitude (L) and the heliocentric radius vector (R) for successive values of V within a given time-span. However, none of the major superior planets have sidereal periods that are shorter than five years thus the computation of each orbit entails the use of successive five-year data sets. For one complete orbit of Jupiter, a minimum of two sets of data is required; for Saturn five, Uranus seventeen, and for Neptune thirty-three. For the interval 1600 - 2100 BP, one hundred consecutive sets of power series data are therefore required for each planet.

B. THE FOUR TERRESTRIAL PLANETS
In contrast to the relatively simple power-series methodology for the major superior planets formulas for the terrestrial planets are both cumbersome and difficult to implement in times-series format without the heavy use of computing devices. Here the formulas vary from planet to planet and all require tables and lengthy trigonometric summations. For example, for Mercury alone the formulas and tables for the heliocentric radius vector (R), the heliocentric latitude (B), and the heliocentric longitude (L) are:

  MERCURY: HELIOCENTRIC RADIUS VECTOR ( R )

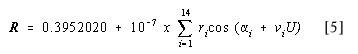
Relation 5r. Heliocentric Distance (Mercury)
TABLE: i = 1 to 14

i ri ai vi
1 780141 6.202782 260878.753962
2 78942 2.98062 521757.50830
3 12000 6.0391 782636.264 0
4 9839 4.8422 260879.380 8
5 2355 5.062 0.734
6 2019 2.898 1 043514.987
7 1974 1.588 521758.140
8 1859 0.805 260877.716
9 426 4.601 782636.915
10 397 5.976 1 304393.735
11 382 3.86 521756.47
12 306 1.87 1 043515.34
13 102 0.62 782635.28
14 92 2.60 1 565272.52


  MERCURY: HELIOCENTRIC LATITUDE ( B )

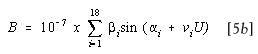
Relation 5b. Heliocentric Latitude (Mercury 

 

  TABLE: i = 1 to 18

i bi ai vi
1 680303
 3.82625
 260879.17693
2 538354
 3.30009
 260879.66625
3 176935
 3.74070
 0.40005
4 143323
 0.58073
 521757.92658
5 105214
 0.05450
 521758.44880
6 91011
 3.3915
 0.9954
7 47427
 1.9266
 260878.2610
8 41669
 3.5084
 782636.7624
9 19826
 3.1539
 782637.4813
10 12963
 0.2455
 1043515.6610
11 8233
 4.886
 521756.972
12 6399
 0.358
 782637.769
13 3196
 3.253
 1304394.380
14 1536
 4.824
 1043516.451
15
 824
 0.04
 1565273.15
16 819
 1.84
 782635.45
17 324
 1.60
 1304395.53
18 201
 2.92
 1826151.86


 MERCURY: HELIOCENTRIC LONGITUDE ( L )

 L = 4.4429839 + 260881.4701279U

+10-6{(409894.2+2435U-1408U 2 +114U 3 +233U 4 -88U 5 )

x sin(3.053817+260878.756773U-0.001093U 2 +0.00093U 3+0.00043U 4+0.00014U 5)}

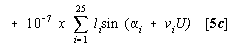
Relation 5c: Heliocentric Longitude for Mercury

TABLE: i = 1 to 25

i Li ai vi
1 510728
 6.09670
 521757.52364
2 404847
 4.72189
 1.62027
3 91048
 2.8946
 782636.2744
4 30594
 4.1535
 521758.6270
5 15769
 5.8003
 1043515.0730
6 13726
 0.4656
 521756.9570
7 11582
 1.0266
 782638.007
8 7633
 3.517
 521759.335
9 5247
 0.418
 1043516.352
10 4001
 3.993
 1304393.680
11 3299
 2.791
 1043514.724
12 3212
 0.209
 1304394.627
13 1690
 2.067
 1304395.168
14 1482
 6.174
 782635.409
15
 1233
 3.606
 1043516.88
16 1152
 5.856
 1565272.646
17 845
 2.63
 1565273.50
18 654
 3.40
 1826151.56
19 359
 2.66
 11094.77
20 356
 3.08
 1565273.50
21 257
 6.27
 1826152.20
22 246
 2.89
 5.41
23 180
 5.67
 56613.61
24 159
 4.57
 250285.49
25 137
 6.17
 271973.50

HELIOCENTRIC RADIUS VECTORS: VENUS, SUN (EARTH), AND MARS
In so much as the present paper is an introduction rather than a detailed description the corresponding formulas and tables for the longitudes and latitudes of the other terrestrial planets will not be presented here in toto. For general information, however, a limited treatment of the remaining heliocentric radius vectors for this trio of planets is shown below; for further details refer to the descriptions and explanations provided by Bretagnon and Simon (1986).

 VENUS: HELIOCENTRIC RADIUS VECTOR (R)

 R = 0.723 5481 + 10 -7 {(48982 - 34549U + 7096U 2 3360U 3 + 890U 4 - 210U 5)

x cos(4.02152 + 102132.84695U + 0.2420U 2 + 0.0994U 3 + 0.0351U 4 - 0.0013U 5 - 0.015U 6)}

+ 10-7{(166-234U + 131U 2) x cos(4.90 + 204265.69U + 0.48U 2 + 0.20U 3)}

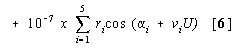
Relation 6: Heliocentric Distances for Venus
   


TABLE: i = 1 to 5

i ri ai vi
1 72101 2.828 0.361
2 163 2.85 78604.20
3 138 1.13 117906.29

50 2.59 96835.94
5 37 1.42 39302.10


SUN (EARTH): HELIOCENTRIC RADIUS VECTOR (R)

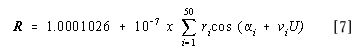
Relation 7. Heliocentric Radius Vector (Earth)
 

 
 [Table: i = 1 to 50 omitted ]

MARS: HELIOCENTRIC RADIUS VECTOR (R)

R = 1.5298560 + 10-6{(141 849.5 + 13651.8U - 1230U 2 - 378U 3 + 187U 4 - 153U 5 - 73U 6)

cos(3.479698+33405.349560U+0.030669U2 -0.00909U3+0.00223U4 +0.00083U5 -0.00048U6)}

+ 10-6{(6607.8 + 1272.8U - 53U 2 - 46U 3 + 14U 4 - 12U 5 + 99U 6)x

cos(3.81781 + 66810.6991U + 0.0613U 2 - 0.0182U 3 + 0.0044U 4 + 0.0012U 5 + 0.002U 6)}

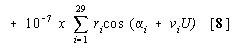
Relation 8: Heliocentric Distances for Mars
 
 

[Table: i = 1 to 29 omitted ]

TIME
As before, Ephemeris Time (ET); the variable (U)t derived from the following relation: 


C. HELIOCENTRIC RADIUS VECTORS
Although relations [9] and [4] require corrections for historical research [i.e., to obtain Ephemeris Time (ET) from Universal Time (UT]), for present purposes it proves useful to remain with julian dates throughout since the latter lend themselves readily to computational techniques (i.e., looping, incrementations, etc) in a variety of complex applications. Moreover, although it still remains feasible to calculate the planetary positions by applying related formulas for the heliocentric distances, longitudes and latitudes in a standard manner, it is the heliocentric distances that are by far the most useful.

The exact, sequential value for the radius vector of a planet moving in an elliptical orbit carries with it both the corresponding orbital velocity and the corresponding orbital "period" for the exact position and time in question. In other words, a variable radius vector that moves between the limits established by the points of perihelion and aphelion provides two further and related time-series functions. The first describes the manner in which the radius vector changes, the second the orbital velocity itself, and the third - though not immediately apparent - the corresponding "range" of the period of revolution. To put the latter in a clearer light, the synodic time between a pair of co-orbital planets - essentially the time a faster moving inner planet ( mean orbital period T1 ) takes to lap a slower outer planet ( mean orbital period T2 ) may be obtained from the general synodic formula:
Relation 10: The General Synodic Formula for Co-Orbital Bodies

However, in practice, adjacent pairs of planets are rarely at the particular points in their orbits that correspond to mean value radius vectors. Thus the mean synodic period remains basically a theoretical parameter. From a more practical viewpoint, however, for every value of the radius vector between perihelion and aphelion there are corresponding "periods" of revolution, and as a consequence real-time synodic functions may be determined directly from such radius vectors by the application of the Harmonic Law ( T 2 = R 3 ). For the superior planets this poses no great problem since true radius vectors may be obtained from the power series data and associated tables in a relatively straightforward manner. For the terrestrial planets the same basic approach holds except that more complex formulas and tables are involved. Both methods, however, lend themselves readily to looping and incrementation, and all provide the means for investigating interactive relationships. Examples of the latter include the visualization of the well known 2 : 1 Earth-Mars and 2 : 5 Jupiter-Saturn resonances, the relationship between difference in the inverse orbital velocities of the latter pair and the orbital velocity of Mars; and further complexities associated with Venus-Earth-Mars resonances. See Times Series Graphics for examples, especially the latter.
SOURCE
Part C and Relation 10 excepted, the above formulas, tables, power series data and general methodology are from Bretagnon and Simon (1986), i.e.,

TABLES FOR THE MOTION OF THE SUN AND THE FIVE PLANETS FROM - 4000 TO + 2800
TABLES FOR THE MOTION OF URANUS AND NEPTUNE FROM + 1600 TO + 2800
Pierre Bretagnon and Jean-louis Simon
Service des Calculs et de Mécanique Céleste du Bureau des Longitudes
77, avenue Denfert-Rochereau, 75014 Paris, France.

Published by Willmann-Bell, Inc., Richmond, 1986.

John N. Harris. Last updated July16, 2004.

Return to Spira Solaris [] Times Series Graphics