FORM AND PHYLLOTAXIS
It is well known that the arrangement of the leaves in plantsmay be expressed by very simple series of fractions, all of which are gradual approximations to, or the natural means between 1/2 or 1/3, which two fractions are themselves the maximum and the minimum divergence between two single successive leaves. The normal series of fractions which expresses the various combinations most frequently observed among the leaves of plants is as follows: 1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, 21/55, etc. Now upon comparing this arrangement of the leaves in plants with the revolutions of the members of our solar system, Peirce has discovered the most perfect identity between the fundamental laws which regulate both. 1
(Louis Agassiz, ESSAY ON CLASSIFICATION, Ed. E. Lurie, Belknap Press, Cambridge, 1962:127; emphases supplied)
II. INTRODUCTION
III. BENJAMIN PEIRCE, PHYLLOTAXIS, AND THE SOLAR SYSTEM
IV. THE PHYLLOTACTIC SOLAR SYSTEM
IV.1. PHYLLOTACTIC DIVISORS AND SYNODIC PERIODS
IV.2. THE DUPLICATED DIVISORS
V. PHYLLOTAXIS AND THE PHI-SERIES
IV. IMPLICATIONS AND RAMIFICATIONS
I. PRELIMINARY REMARKS
Initially this matter is simple enough:
Either the Solar System is phyllotactic in nature, as Benjamin Peirce intimated over one hundred and fifty years ago, or it is not.
Whether Benjamin Peirce's conclusions should have been accepted at that time (or at least received a better airing) is a different matter altogether. Then again, this paper is not an historical commentary per se, nor is it concerned with the religious elements evident in Louis Agassiz' Essay on Classification, or similar concerns (if that is what they truly are) expressed in Benjamin Peirce's retirement speech to the membership of the AAAS in 1853.
In short, it is the data and the methodology applied by Benjamin Peirce that will be re-examined here and ultimately re-worked for modern consumption.
II. INTRODUCTION
Assigned to the title heading SPIRA SOLARIS this January 2007 conclusion owes its origins to a number of events and issues, but the subtitle itself ( Form and Phyllotaxis ) arises from the neglected Solar System researches of American mathematician Benjamin Peirce (1809-1890). Perhaps serendipitously, his investigation and conclusions resurfaced in September 2006 as a consequence of the official elevation of the asteroid Ceres and demotion of the planet Pluto to the status of "Dwarf Planets." Essentially,with Pluto thus demoted Neptune once more becomes the outermost planet, as Peirce had stipulated on theoretical grounds over 150 years ago. First published in 18502 and later recorded by his friend Louis Agassiz (1807-1873) in the latter's famousEssay on Classification (1857:131) Peirce had declared that "there can be no planet exterior to Neptune, but there may be one interior to Mercury." 3 revisiting my own attempts to come to terms with the structure of the Solar System in the first three sections of Spira Solaris Archytas-Mirabilis the similarities between the two approaches now suggested that while I had unknowingly followed Peirce by omitting Pluto and also adding an Inter Mercurial object,4 I had nevertheless missed the point entirely when it came to the significance of Neptune. Not so Benjamin Peirce. Nevertheless, although Agassiz provided additional details in his Essay on Classificationconcerning the latter's Solar System research including "the ratios of the laws of phyllotaxis" 5 in this same astronomical context, Peirce's major conclusion was cast aside despite its implications. Although not stated in these precise terms, it was nothing less than the perception that
"Modern science has realized some of the most fanciful of the Pythagorean and Platonic doctrines, and thereby justified the divinity of their spiritual instincts. Is it not significant of the nature of the creative intellect, the simplicity of the great laws of force? the fact that the same curious series of numbers is developed by the growing plant which assisted in marshalling the order of the planets? and that the marriage of the elements cannot be consummated except in strict accordance with the laws of definite proportion? ” (Address of Professor Benjamin Peirce, President of the Association of the American Association for the Year 1853, on retiring from the duties of President. 1853:6–7;"Printed by Order of the Association." (The Cornell Library Historical Mathematics Monographs (JPG) emphases supplied. Html version: Peirce 1853 ).
PEIRCE,
BENJAMIN
(b.
Salem,
Mass., 1809; d. Cambridge, Mass., 1880), mathematics, astronomy.
Graduated from
Harvard (1829;
M.A., 1833), where he was a tutor
(
1831–33) and professor (1832–80). In mathematics, he amended N.
Bowditch's translation of Laplace's (1829-39);
proved (1832) that there is no odd
perfect number with fewer than four prime factors; published popular
elementary textbooks; discussed possible systems of multiple algebras
in Mécanique
célesteLinear
Associative Algebra ... and
set forth, in A
System of Analytic
Mechanics (1855), the
principles and methods of that science as
a branch of mathematical theory, developed from the idea of the
"potential." In astronomy, he studied comets; worked on revision of
planetary theory and was the first to compute the perturbing influence
of other planets on Neptune; and worked on the mathematics of the rings
of Saturn, deducing that they were fluid. From 1852 he worked with the
U.S. Coast Survey on longitude determination, ... became head of the
survey (1867-74) (and) superintended measurement of the arc of the
thirty-ninth parallel in order to join the Atlantic and Pacific systems
of triangulation. Influential in founding the Smithsonian Institution
and the National Academy of Sciences. (Concise
Dictionary of
Scientific Bibliography,
Charles Scribner’s Sons, New York,
1981:540)
The full description of Benjamin Peirce's application of the Fibonacci series to the structure of the Solar System as published by Louis Agassiz is provided below; perhaps significantly, the words "Fibonacci" and "Golden Section" are noticeably absent -- such words perhaps already unacceptable to the powers that be and also a perceived threat to the status quo. Nevertheless, there can be no mistaking the sequence applied or the major premise, called here fittingly enough (for the moderns, at least) "the law of phyllotaxis". One may also note that Peirce had already considered the practical differences between his theoretical treatment and the Solar System itself and subsequently considered not only the position of Earth, but also discrepancies encountered for the positions of Mars, Uranus and Neptune. Initially Pierce also applied a double form of Fibonacci series but subsequently reduced the set to arrive are a situation similar to that involving the synodic difference cycle between adjacent planets.
That he did not examine the matter from this particular viewpoint in greater detail is the reason why this present essay exists.
III. BENJAMIN PEIRCE, PHYLLOTAXIS, AND THE SOLAR SYSTEM
ESSAY ON CLASSIFICATION 8
Louis Agassiz 1857
FUNDAMENTAL RELATIONS OF ANIMALS
SECTION XXXI
COMBINATIONS IN TIME AND SPACE OF VARIOUS KINDS OF RELATIONS AMONG ANIMALS
It must occur to every reflecting mind, that the mutual relation and respective parallelism of so many structural, embryonic, geological, and geographical characteristics of the animal kingdom are the most conclusive proof that they were ordained by a reflective mind, while they present at the same time the side of nature most accessible to our intelligence, when seeking to penetrate the relations between finite beings and the cause of their existence.
The phenomena of the inorganic world are all simple, when compared to those of the organic world. There is not one of the great physical agents, electricity, magnetism, heat, light, or chemical affinity, which exhibits in its sphere as complicated phenomena as the simplest organized beings; and we need not look for the highest among the latter to find them presenting the same physical phenomena as are manifested in the material world, besides those which are exclusively peculiar to them. When then organized beings include everything the material world contains and a great deal more that is peculiarly their own, how could they be produced by physical causes, and how can the physicists, acquainted with the laws of the material world and who acknowledge that these laws must have been established at the beginning, overlook that à fortiori the more complicated laws which regulate the organic world, of the existence of which there is no trace for a long period upon the surface of the earth, must have been established later and successively at the time of the creation of the successive types of animals and plants?
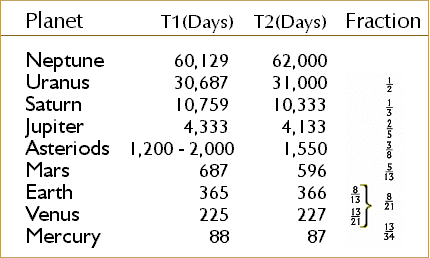
Thus far we have been considering chiefly the contrasts existing between the organic and inorganic worlds. At this stage of our investigation it may not be out of place to take a glance at some of the coincidences which may be traced between them, especially as they afford direct evidence that the physical world has been ordained in conformity with laws which obtain also among living beings, and disclose in both spheres equally plainly the workings of a reflective mind. It is well known that the arrangement of the leaves in plants148 may be expressed by very simple series of fractions, all of which are gradual approximations to, or the natural means between 1/2 or 1/3, which two fractions are themselves the maximum and the minimum divergence between two single successive leaves. The normal series of fractions which expresses the various combinations most frequently observed among the leaves of plants is as follows: 1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, 21/55, etc. Now upon comparing this arrangement of the leaves in plants with the revolutions of the members of our solar system, Peirce has discovered the most perfect identity between the fundamental laws which regulate both, as may be at once seen by the following diagram, in which the first column gives the names of the planets, the second column indicates the actual time of revolution of the successive planets, expressed in days; the third column, the successive times of revolution of the planets, which are derived from the hypothesis that each time of revolution should have a ratio to those upon each side of it, which shall be one of the ratios of the law of phyllotaxis; and the fourth column, finally, gives the normal series of fractions expressing the law of the phyllotaxis.149><>
Table I (Peirce-Agassiz 1857; column titles added)
Let us therefore repeat our diagram in another form, the third column giving the theoretical time of revolution.
Table II (Peirce-Agassiz 1857; column titles added)
It appears from this table that two intervals usually elapse between two successive planets, so that the normal order of actual fractions, 1/2, 1/3, 2/5, 3/8, 5/13, etc., or the fractions by the short way in phyllotaxis, from which, however, the Earth is excluded, while it forms a member of the series by the long way. The explanation of this, suggested by Peirce, is that although the tendency to set off a planet is not sufficient at the end of a single interval, it becomes so strong near the end of the second interval that the planet is found exterior to the limit of this second interval. Thus, Uranus is rather too far from the Sun relatively to Neptune, Saturn relatively to Uranus, and Jupiter relatively to Saturn; and the planets thus formed engross too large a proportionate share of material, and this is especially the case with Jupiter. Hence, when we come to the Asteroids, the disposition is so strong at the end of a single interval, that the outer Asteroid is but just within this interval, and the whole material of the Asteroids is dispersed in separate masses over a wide space, instead of being concentrated into a single planet. A consequence of this dispersion of the forming agents is that a small proportionate material is absorbed into the Asteroids. Hence, Mars is ready for formation so far exterior to its true place, that when the next interval elapses the residual force becomes strong enough to form the Earth, after which the normal law is resumed without any further disturbance. Under this law there can be no planet exterior to Neptune, but there may be one interior to Mercury.
Let us now look back upon some of the leading features alluded to before, omitting the simpler relations of organized beings to the world around, or those of individuals to individuals, to consider only the different parallel series we have been comparing when showing that in their respective great types the phenomena of animal life correspond to one another, whether we compare their rank as determined by structural complication with the phases of their growth, or with their succession in past geological ages; whether we compare this succession with their embryonic growth, or all these different relations with each other and with the geographical distribution of animals upon earth. The same series everywhere! These facts are true of all the great divisions of the animal kingdom, so far as we have pursued the investigation; and though, for want of materials, the train of evidence is incomplete in some instances, yet we have proof enough for the establishment of this law of a universal correspondence in all the leading features which binds all organized beings of all times into one great system, intellectually and intelligibly linked together, even where some links of the chain are missing. It requires considerable familiarity with the subject even to keep in mind the evidence, for, though yet imperfectly understood, it is the most brilliant result of the combined intellectual efforts of hundreds of investigators during half a century. The connection, however, between the facts, it is easily seen, is only intellectual; and implies therefore the agency of Intellect as its first cause. 150
And if the power of thinking connectedly is the privilege of cultivated minds only; if the power of combining different thoughts and of drawing from them new thoughts is a still rarer privilege of a few superior minds; if the ability to trace simultaneously several trains of thought is such an extraordinary gift, that the few cases in which evidence of this kind has been presented have become a [p.131] matter of historical record (Caesar dictating several letters at the time), though they exhibit only the capacity of passing rapidly, in quick succession, from one topic to another, while keeping the connecting thread of several parallel thoughts: if all this is only possible for the highest intellectual powers, shall we by any false argumentation allow ourselves to deny the intervention of a Supreme Intellect in calling into existence combinations in nature, by the side of which all human conceptions are child's play?
If I have succeeded, even very imperfectly, in showing that the various relations observed between animals and the physical world, as well as between themselves, exhibit thought, it follows that the whole has an Intelligent Author; and it may not be out of place to attempt to point out, as far as possible, the difference there may be between Divine thinking and human thought. Taking nature as exhibiting thought for my guide, it appears to me that while human thought is consecutive, Divine thought is simultaneous, embracing at the same time and forever, in the past, the present, and the future, the most diversified relations among hundreds of thousands of organized beings, each of which may present complications again, which, to study and understand even imperfectly, as for instance, Man himself, Mankind has already spent thousands of years. And yet, all this has been done by one Mind, must be the work of one Mind only, of Him before whom Man can only bow in grateful acknowledgment of the prerogatives he is allowed to enjoy in this world, not to speak of the promises of a future life.
I have intentionally dismissed many points in my argument with mere questions, in order not to extend unduly a discussion which is after all only accessory to the plan of my work. I have felt justified in doing so because, from the point of view under which my subject is treated, those questions find a natural solution which must present itself to every reader. We know what the intellect of Man may originate, we know its creative power, its power of combination, of foresight, of analysis, of concentration; we are, therefore, prepared to recognize a similar action emanating from a Supreme Intelligence to a boundless extent. We need therefore not even attempt to show that such an Intellect may have originated all the Universe contains; it is enough to demonstrate that the constitution of the physical world and, more particularly, the organization of living beings in their connection with the physical world, prove in general the existence of a Supreme Being as the Author of all things. The task of science is rather to investigate what has been done, to inquire if possible how it has been done, than to ask what is possible for the Deity, as we can know that only by what actually exists. To attack such a position, those who would deny the intervention in nature of a creative mind must show that the cause to which they refer the origin of finite beings is by its nature a possible cause, which cannot be denied of a being endowed with the attributes we recognize in God. Our task is therefore completed as soon as we have proved His existence. It would nevertheless be highly desirable that every naturalist who has arrived at similar conclusions should go over the subject anew from his point of view and with particular reference to the special field of his investigations; for so only can the whole evidence be brought out. I foresee already that some of the most striking illustrations may be drawn from the morphology of the vegetable kingdom, especially from the characteristic succession and systematical combination of different kinds of leaves in the formation of the foliage and the flowers of so many plants, all of which end their development by the production of an endless variety of fruits. The inorganic world, "considered in the same light, would not fail to exhibit also unexpected evidence of thought, in the character of the laws regulating the chemical combinations, the action of physical forces, the universal attraction, etc., etc. Even the history of human culture ought to be investigated from this point of view. But I must leave it to abler hands to discuss such topics.SECTION XXXI
RECAPITULATION
Last Section (31st)<> 31st. The combination in time and space of all these thoughtful conceptions exhibits not only thought, it shows also premeditation, power, wisdom, greatness, prescience, omniscience, providence. In one word, all these facts in their natural connection proclaim aloud the One God, whom man may know, adore, and love; and Natural History must in good time become the analysis of the thoughts of the Creator of the Universe, as manifested in the animal and vegetable kingdoms, as well as in the inorganic world.
<> It may appear strange that I should have included the preceding disquisition under the title of an "Essay on Classification." Yet it has been done deliberately. In the beginning of this chapter I have already stated that Classification seems to me to rest upon too narrow a foundation when it is chiefly based upon structure. Animals are linked together as closely by their mode of development, by their relative standing in their respective classes, by the order in which they have made their appearance upon earth, by their geographical distribution, and generally by their connection with the world in which they live, as by their anatomy. All these relations should therefore be fully expressed in a natural classification; and though structure furnishes the most direct indication of some of these relations, always appreciable under every circumstance, other considerations should not be neglected which may complete our insight into the general plan of creation. (Louis Agassiz, ESSAY ON CLASSIFICATION, Ed. E. Lurie, Belknap Press, Cambridge, 1962:127-128)
IV.THE PHYLLOTACTIC SOLAR SYSTEM
But in any event it is the location of Neptune that provides the key to Benjamin Peirce's far-reaching understanding of the matter. This I failed to comprehend when I first added the latter's material to Part VI owing to a basic difference in methodology. The inner starting point adopted by myself was perhaps always likely to produce the Pheidian Framework, but might not necessarily shed light on the final phyllotactic aspect. Starting from the opposite end, however, onecommences with the latter, and with the larger fibonacci fractions applied by Peirce, one also moves with increasing accuracy towards the constant of linearity, Phi. Thus starting from this direction was (in retrospect) always likely to be more productive. In one sense, however, Peirce's approach may have appeared almost too simplistic with divisions involving periods of revolution expressed in days and the unexpected constant duplication of his divisors. The reason behind this latter occurrence is more complex than one might suspect since it is intimately related to intermediate synodic periods between adjacent pairs of planets. However, since the latter are simply obtained from the general synodic formula (the product of the two periods of revolution divided by their difference; see Part II), one can readily test the paired divisors applied Peirce from this particular viewpoint. Thus in Table 1 below the fibonacci fractions employed by Peirce are applied firstly to the mean period of revolution of Neptune (given here as 164.62423 years, i.e., Peirce's 60,129 days divided by365.25 days). Thereafter the divisions continue sequentially from the previous result, i.e., division by 1 again, by1/2, 1/2, then 2/3, 2/3, etc., down to the final divisor 21/34 to obtain the mean sidereal period of Mercury. Further division could, of course, follow with another division by 21/34 and the application of the next divisor (34/55), etc., as far as one might wish.
IV.1. THE PHYLLOTACTIC DIVISORS AND SYNODIC PERIODS

Table 3. Benjamin Peirce's Phyllotactic Divisors
We come now to the underlying reason why the divisors applied by Benjamin Peirce occur in pairs, though not from any a priori or phyllotactic viewpoint. Although perhaps not immediately obvious, the pairings concern matters that have long been known, namely resonances between adjacent pairs of planets. For example, one of the better known planetary resonances concerns the relative motion of Jupiter with respect to Saturn, specifically, a 2:3:5 fibonacci resonance that occurs after approximately 60 years when slower-moving Saturn (mean period of revolution 29.45252 years) completes 2 sidereal revolutions around the centre of the Solar System (for present purposes, simply the Sun) with swifter-moving Jupiter (mean period of revolution11.869237 years) completing 5 sidereal revolutions about the same centre while also lapping Saturn 3 times (lap cycle:19.88813 years), resulting in a resonant triple with the three periods expressed in the form 2:3:5. The same procedures can be carried out on the remaining superior planets, but in view of the elliptical nature of planetary orbits the application of mean motion is a vast over-simplification, as the real-time investigations carried out in Part III of Spira Solaris Archytas-Mirabilis showed (seePart III, Figures 8-8b; and Figure 1 below for the real-time Jupiter-Saturn and Uranus-Neptune Resonances from 1940-1990).
IV. 3. THE EXTENDED PHI-SERIES AND THE INNER LIMIT
Once these resonant relationships are seen for what they are, however, it is clear that Benjamin Peirce was indeed correct about the occurrence of Fibonacci fractions in the the Solar System, and it is also clear why he took Neptune to be the outermost limiting planet, i.e., the resonant triples necessarily commence with the first three fibonacci numbers (1,1,2,3,5,8,13,21,34,55,89, etc.) and increase accordingly. But there is far more to this matter for the three resonant triples 1:1:2, 1:2:3and 2:3:5 associated with the four superior planets Neptune, Uranus, Saturn and Jupiter are not only sequential, they are also successive Fibonacci triples bound together in a most complex manner.
Before moving on to the last issue a question naturally arises whether an inner limit exists, and whether this might be determined. Even so, with Neptune "accounted for" there still remain two additional anomalous regions to complicate matters, but once again the elevation of Ceres to the status of Dwarf planet at least fills the next region below Jupiter, though still leaving the "anomalous" location of Earth to be resolved. Fortunately, however, the inclusion of Ceres provides two further sequential resonant triples (3:5:8 and5:8:13 respectively) while the Phi-Series planetary framework also renders assistance below Mercury, since (in theoretical terms at least) it is only a matter of decreasing exponents by unity to move inwards as far as one wishes. In this manner it becomes possible to suggest that the resonant triples not only extend sequentially downwards from Neptune to Mercury (resonant triple 13:21:34) but also beyond Mercury to a specific limit at the fifth inner position (final resonant triple of 144:233:377) as seen below in Table 4 for Phi-Series periods Phi 5 through Phi -13
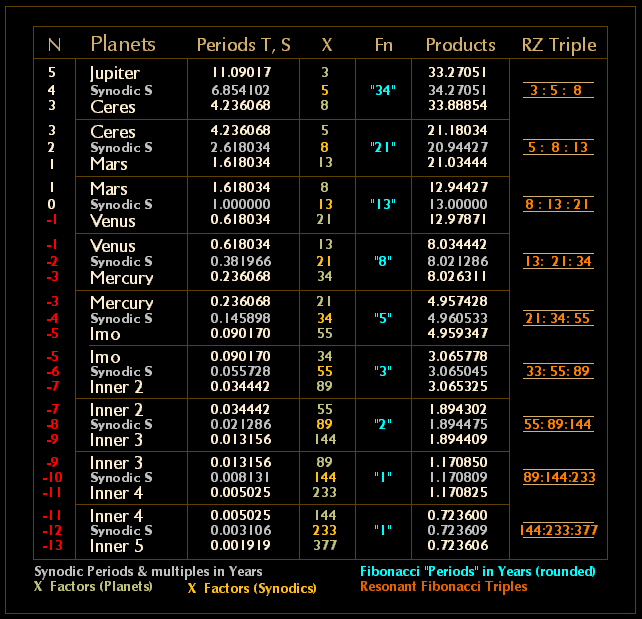
In Table 4 it is the pairings that that are duplicated, not the divisors. Some columns are self-explanatory, e.g., the Phi-Series exponents in Column N, as are the resulting sidereal (T) and synodic periods (S) although in the latter case they are generated by the even-numbered exponents rather than the more usual general synodic formula - just one more facet of an already complex dynamic matter. The parameters in Column X are the numbers of complete sidereal revolutions and synodic cycles per pairing (i.e., sidereal and synodic X-Factors), while (omitting Column FN for the time being) the data in the Products and the RZ Triples are exactly that, with the latter also theX-Factors from the X Column.
The rounded periods in Column Fn require some explanation, although the perceptive reader may have already seen that the closer the Products get to the Inner Limit, the more obvious it becomes that the former in every instance are consistent approximations for sequential, fractional exponential values of Phi, e.g., the lowest (0.723606) approximates Phi -2/3 = 0.72556, the next (1.17085) Phi 1/3 = 1.17398, followed by 1.8944 ( Phi 4/3 = 1.89954 ), then 3.065 ( Phi7/3 = 3.0735) and so on, thus the exponents increase by unity with each sidereal pairing. It is also clear from these lower products that for integer values expressed in years, rounding alternates between each pairing (i.e., 0.72360 rounded up = 1, 1.1708 rounded down = 1, 1.8944 rounded up = 2, 3.065 rounded down = 3, etc., producing yet again the Fibonacci Series from the initial commencement point. Lastly, the period below Inner 5 would be Phi -14 with the product obtained from central value of the previous pairing (233) which in turn rounds down to zero. Hence the suggestion that the Inner 5 position provides the innermost limit.
Applying the same techniques to Solar Systen mean values for Mars, Ceres and the four superior planets results in a similar, but not identical pattern, for although the alternative rounding continues in sequence as far as the lower products of the Jupiter -Saturn pairing, beyond this pair the products increasing diverge from the rounded Fibonacci Periods, as do the last pair of resonant triples:
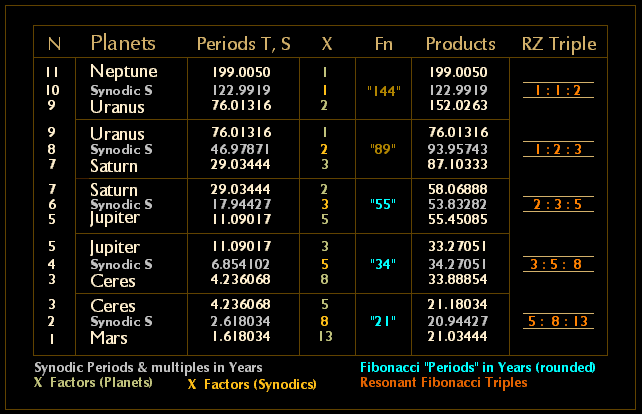
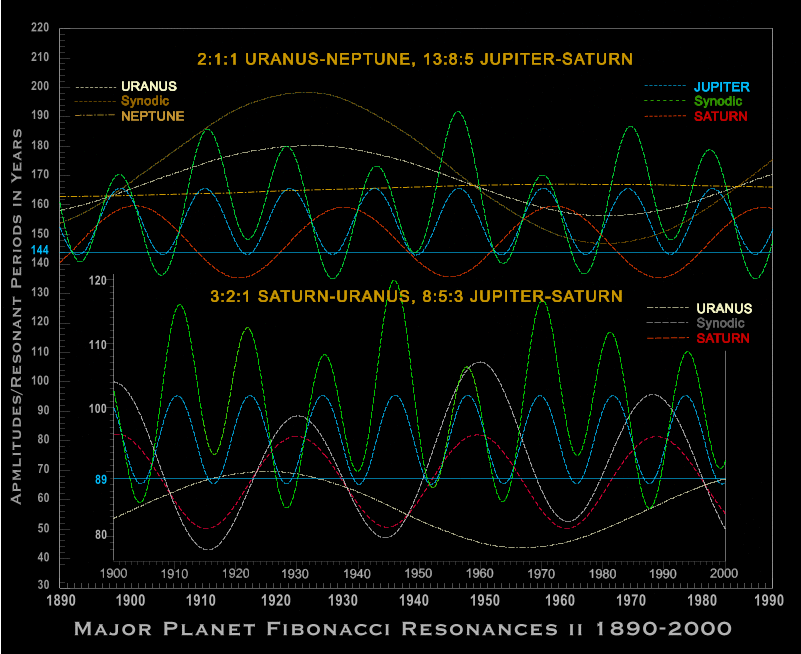
Figure 1. Jupiter-Saturn-Uranus-Neptune real-time Fibonacci Resonances I, 1890-1990
IV.4. SOLAR SYSTEM RESONANT PHYLLOTACTIC TRIPLES
At which point we return to the divisions obtained by Benjamin Peirce and consider next the overall Solar System from Mercury to Neptune with Pluto omitted, Ceres included and Earth in a synodic location between Mars and Venus as applied in Tables 4 and 5.
Thus in Table 6 below the mean sidereal periods of revolution and intervening mean synodic periods are multiplied by the corresponding X-Factors (numbers of mean sidereal and mean synodic periods) to produce the resonant period for each pair of planets with the latter also providing the corresponding Resonant (RZ) Triples. There is more that could be shown here, including resonant triple variants for Earth and its bracketing synodic periods, and also further investigations involving slightly improved correspondances obtained from the use of aphelion and and perihelion periods rather than mean values.
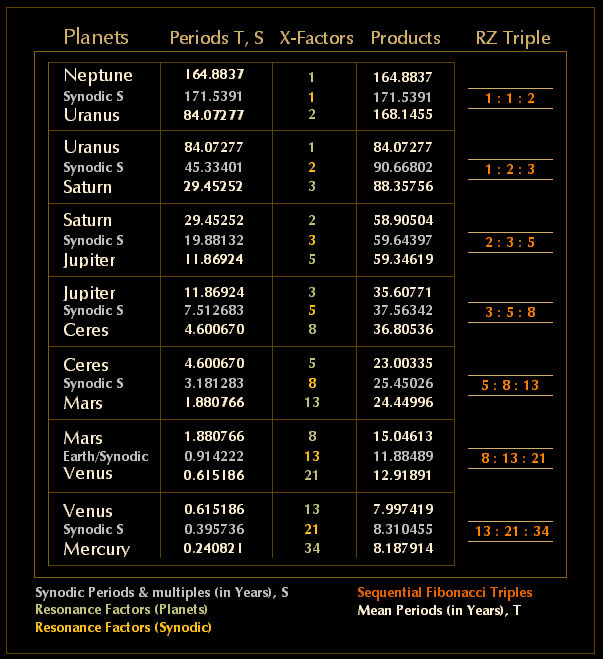
Table 6.Resonant Phyllotactic Triples, Mercury to Neptune (Mean values; Ceres included, Earth Synodic)

Figure 2. Phyllotactic Resonant Triples in the Solar System
Although it is the synodic cycle that binds each individual pair, it is clear from the resonant triples and the lower right insert that the middle number of the first triple (the number of Neptune-Uranus synodics) is the same as the firstvalue of the next triple (the number of sidereal revolutions ofUranus), and that the last value of the first triple (also the number of revolutions of Uranus in the first set) is the middlevalue of the next (i.e., the numbers of Uranus-Saturn synodics) and that this is a consistent pattern that links the resonant triples throughout. Which in passing is more than faintly reminiscent of details and relationships furnished in Plato'sTimaeus 31b-32c, though this is not our current concern here.
V. PHYLLOTAXIS AND THE PHI-SERIES
What remains now is the relationship between Benjamin Peirce's divisors, the Phi-Series, and the application of phyllotaxis to the structure of the Solar System.
The above somewhat limited discussion necessarily concerns complex waveforms and motions for the mean, varying and extremal values dictated by elliptical orbits. Although one could suggest that both the Fibonacci and the Lucas Series are embedded in the Solar System, it might be more accurate to say that they are in fact pulsating through it, and perhaps have been since time immemorial. That this inquiry should eventually lead to planetary resonances involving both the Lucas and the Fibonacci Series is hardly surprising given the prominence of the mathematical relationships known to exist between the two series (see, for example The Lucas Numbers and Phi - More Facts and Figures detailed by Dr. R. Knott). What is different here, however, is that the known relations that combine the two series occur in a specific and distinct astronomical context -- not only with respect to the residual elements of Solar System -- but also with respect to the theoretical Phi-Series exponential planetary framework such that (a) the two major period constants ( PhiandPhi 2 ):
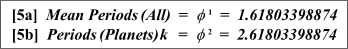
re-occur in the form of the double Fibonacci sequence, and (b), the proximity of theLucas Series to the Phi-Series becomes increasingly apparent as thePhi-Series planetary periods increase from Jupiter onwards and outwards (i.e.,Lucas 11 : Phi-Series 11.09016994; Lucas 29 : Phi-Series 29.03444185, etc.):
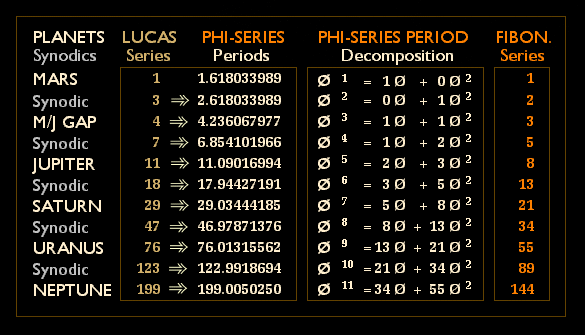
Thus we already encounter in the Phi-seriesplanetary framework complex dynamic relationships between the two inner inferior planets and the two largest superior planets involving constants known to be intimately related to phyllotaxis

To put the full significance of the Phi-Seriesplanetary framework and the constants in question in their full perspective it may be useful to include here a discussion pertaining to phyllotaxis from Part III:11
" It has long been recognized that although Phi and the Fibonacci Series are intimately related to the subject of natural growth that they are not limited to these two fields alone. Remaining with the Phi-Series, Jay Kappraff points out that the French architect Le Corbusier "developed a linear scale of lengths based on the irrational number (phi), the golden mean, through the double geometric and Fibonacci (phi) series" for his Modular System. The latter's interest in the topic is explained further in the following informative passage from Kappraff's CONNECTIONS: The Geometric Bridge between Art and Science:
As a young man, Le Coubusier studied the elaborate spiral patterns of stalks, or paristiches as they are called, on the surface of pine cones, sunflowers, pineapples, and other plants. This led him to make certain observations about plant growth that have been known to botanists for over a century.
Plants, such as sunflowers, grow by laying down leaves or stalks on an approximately planar surface. The stalks are placed successively around the periphery of the surface. Other plants such as pineapples or pinecones lay down their stalks on the surface of a distorted cylinder. Each stalk is displaced from the preceding stalk by a constant angle as measured from the base of the plant, coupled with a radial motion either inward or outward from the center for the case of the sunflower [see Figure 3.21 (b)] or up a spiral ramp as on the surface of the pineapple. The angular displacement is called the divergence angle and is related to the golden mean. The radial or vertical motion is measured by the pitch h. The dynamics of plant growth can be described by and h; we will explore this further in Section 6.9 [Coxeter, 1953].
Each stalk lies on two nearly orthogonally intersecting logarithmic spirals, one clockwise and the other counterclockwise. The numbers of counterclockwise and clockwise spirals on the surface of the plants are generally successive numbers from the F series, but for some species of plants they are successive numbers from other Fibonacci series such as the Lucas series. These successive numbers are called the phyllotaxis numbers of the plant. For example, there are 55 clockwise and 89 counterclockwise spirals lying on the surface of the sunflower; thus sunflowers are said to have 55, 89 phyllotaxis. On the other hand, pineapples are examples of 5, 8 phyllotaxis (although, since 13 counterclockwise spirals are also evident on the surface of a pineapple, it is sometimes referred to as 5, 8, 13 phyllotaxis). We will analyze the surface structure of the pineapple in greater detail in Section 6.9.3.7.2 Nature responds to a physical constraint After more than 100 years of study, just what causes plants to grow in accord with the dictates of Fibonacci series and the golden mean remains a mystery. However, recent studies suggest some promising hypotheses as to why such patterns occur [Jean, 1984], [Marzec and Kappraff, 1983], [Erickson, 1983].
A model of plant growth developed by Alan Turing states that the elaborate patterns observed on the surface of plants are the consequence of a simple growth principle, namely, that new growth occurs in places "where there is the most room," and some kind of as-yet undiscovered growth hormone orchestrates this process. However, Roger Jean suggests that a phenomenological explanation based on diffusion is not necessary to explain phyllotaxis. Rather, the particular geometry observed in plants may be the result of minimizing an entropy function such as he introduces in his paper [1990].
Actual measurements and theoretical considerations indicate that both Turing's diffusion model and Jean's entropy model are best satisfied when successive stalks are laid down at regular intervals of 2Pi /Phi 2 radians, or 137.5 degrees about a growth center, as Figure 3.22 illustrates for a celery plant. The centers of gravity of several stalks conform to this principle. One clockwise and one counterclockwise logarithmic spiral wind through the stalks giving an example of 1,1 phyllotaxis.
The points representing the centers of gravity are projected onto the circumference of a circle in Figure 3.23, and points corresponding to the sequence of successive iterations of the divergence angle, 2Pi n/Phi 2, are shown for values of n from 1 to 10 placed in 10 equal sectors of the circle. Notice how the corresponding stalks are placed so that only one stalk occurs in each sector. This is a consequence of the following spacing theorem that is used by computer scientists for efficient parsing schemes [Knuth, 1980].Theorem 3.3 Let x be any irrational number. When the points [x] f, [2x] f, [3x] f,..., [nx] f are placed on the line segment [0,1], the n + 1 resulting line segments have at most three different lengths.Here clock arithmetic based on the unit interval, or mod 1 as mathematicians refer to it, is used, as shown in Figure 3.24, in place of the interval mod 2pi around the plant stem. It turns out that segments of various lengths are created and destroyed in a first-in-first-out manner. Of course, some irrational numbers are better than others at spacing intervals evenly. For example, an irrational that is near 0 or I will start out with many small intervals and one large one. Marzec and Kappraff [1983] have shown that the two numbers 1/Phi and 1/Phi2 lead to the "most uniformly distributed" sequence among all numbers between Phi and 1. These numbers section the largest interval into the golden mean ratio,Phi :l, much as the blue series breaks the intervals of the red series in the golden ratio.
Moreover, [(n + 1)x]f will fall into one of the largest existing segments. ( [ ] f means "fractional part of ").
Thus nature provides a system for proportioning the growth of plants that satisfies the three canons of architecture (see Section 1.1). All modules (stalks) are isotropic (identical) and they are related to the whole structure of the plant through self-similar spirals proportioned by the golden mean. As the plant responds to the unpredictable elements of wind, rain, etc., enough variation is built into the patterns to make the outward appearance aesthetically appealing (nonmonotonous). This may also explain why Le Corbusier was inspired by plant growth to recreate some of its aspects as part of the Modulor system.(Jay Kappraff, Chapter 3.7. The Golden Mean and Patterns of Plant Growth, CONNECTIONS : The Geometric Bridge between Art and Science, McGraw-Hill, Inc., New York, 1991:89-96, bold emphases supplied.) For more on this topic see also Dr. R. Knott's extensive treatment The Fibonacci Numbers and the Golden Section, the latter's related links and the The Phyllotaxis Home Page of Smith University)
These multiple occurrences arise from the three-fold nature of the Phi-Series Planetary Framework, which necessarily incorporates identical values for periods, distances and velocities according to their exponential position in the framework, including the Inverse Velocities, which (as will be shown later) also play an important role in the computation of angular momentum. From this viewpoint the well-known 60-year, 2 : 3 : 5 fibonacci resonance between the two most massive planets in the Solar system (Jupiter and Saturn) takes on further significance as Figure 8 (21c] shows, for the arithmetic mean of the actual Jupiter and Saturn mean velocities Vr (shown in the upper and lower real-time waveforms) is not only 0.381280708; the daily average function for this pair of planets for the 400-year interval from 1600 - 2000 CE [ 146,000+ data points; Julian Day 2305447.5 through Julian Day 2451544.5 ] is in turn 0.381071579. The figure is necessarily a two-dimensional representation of the orbital motions of the two major Fibonacci planets. Further complications naturally arise from minor differences in the inclination of the planetary planes, periodic changes in the lines of apsides, and the fact that the entire Solar System is (in a temporal sense) also spiraling towards the constellation of Hercules.
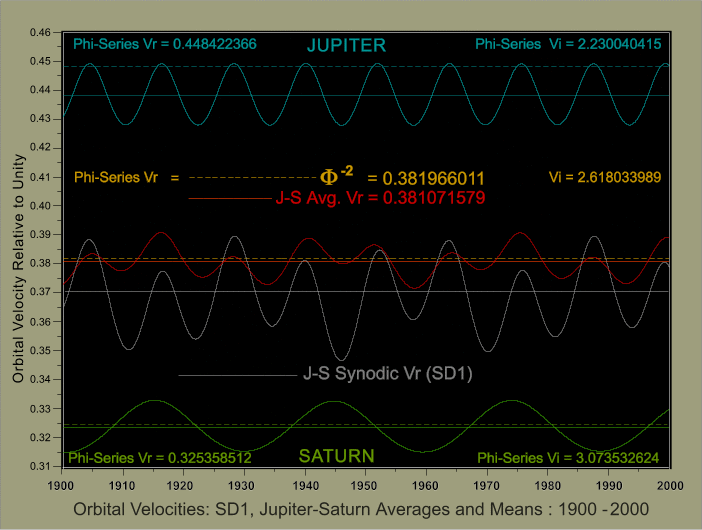
The inclusion of real-time velocities (both relative and inverse) is natural and necessary enough because of the complex dynamic motions involved and they are doubly significant when it is realized that relative to unity angular momentum is in turn the product of the mass and the inverse velocity. Moreover, the role and possible influence of the four superior planets can hardly be ignored given that together the latter provide 99% of the total angular momentum with Jupiter and Saturn alone providing more than 65% of the total.
In passing, as far as the current lack of familiarity in dealing with orbital velocities in the above manner may be concerned, I can only say that almost 18 years have elapsed since my restoration of the velocity components of the laws of planetary motion 10 was published in the Journal of the Royal Astronomical Society of Canada ( "Projectiles, Parabolas, and Velocity Expansions of the Laws of Planetary Motion "JRASC, Vol 83, No. 3, June 1989 ) and that it is disappointing that they have not been put into more general use, especially since the available orbital relationships are effectively quadrupled by their inclusion, i.e.,
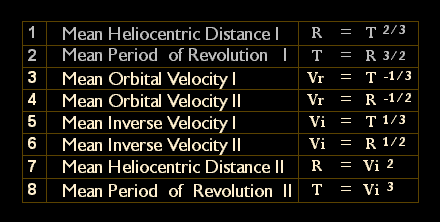
Table 9. Distance-Period-Velocity Relationships
We are at present, it seems, far too pleased with ourselves, and for far too little reason.
But from a wider and larger "organic" perspective we surely need to consider where we ourselves are ultimately headed. And we also need to ask ourselves whether humankind exists in benign and symbiotic relationships with other living organisms (both near and far), or whether our behavior more resembles that of a parasitic infestation, even perhaps to the point of destroying our environment and ourselves. A harsh assessment? Perhaps so, but it is not un-called for in light of our virtually unchecked population growth, our ceaseless depredation of the environment and our worsening cycles of violence. So how indeed do we measure up from this wider and more complex perspective, and what might this augur for future expansion beyond planet Earth? Perhaps more pertinently still, when we ask the perennial question: "Are we Alone?" we might also be wise to ask ourselves whether we are always likely to remain so in view of our unsavoury past, troublesome present, and far from certain future.
Returning to the researches of Benjamin Peirce, in retrospect it is hard to say how far his lines of inquiry might have been extended, or what might ultimately have resulted, but it must surely have been a far more useful endeavor than the circular, simplistic and ad hoc diversions introduced and perpetuated by "Bode's Law." How could something so momentous and far-reaching have been so easily driven into obscurity? According to the modern editor of Agassiz' Essay on Classification, (E. Lurie) it was partly the work of Asa Gray and Chauncey Wright, as explained in the following footnote (the latter's No.149):
Agassiz tried to interest Americans in this concept, an idea typical of German speculative biology and one that he had been much impressed with since his student days at the University of Munich. See Asa Gray, "On the Composition of the Plant by Phytons, and Some Applications of Phyllotaxis," Proceedings, AAAS, II (1850), 438-444, and Benjamin Peirce, "Mathematical Investigations of the Fractions Which Occur in Phyllotaxis," in ibid., 444-447. Gray was never entirely convinced of the validity of this ideal conception. He subsequently encouraged Chauncey Wright to examine the problem of leaf arrangement, with the result that such facts were shown to be understandable in terms of the principle of natural selection.
".. There is a great deal more, of
course, that could be said
concerning the details and the methodology applied to the fitting of
spirals forms to shells and many other natural applications provided in
Sir d'Arcy Wentworth
Thompson's voluminous On Growth
and Form.12 And
indeed in other
works that for a brief time seem to have flourished around the
beginning
of the last century. The above is included here because it epitomizes
the darker, stumbling side of human progress. And also the realization
that when Thomas Taylor (Introduction toLife
and
Theology of Orpheus) speaks of social decline, loss of knowledge in
ancient times and the efforts to preserve it by those who, "though
they lived in a base
age" nevertheless"happily
fathomed the depth of their great master's works, luminously and
copiously developed their
recondite meaning, and benevolently communicated it in their writings
for the general good," that sadly, such times are still upon
us. Thus, just as Sir Theodore Andrea Cook,13who in the Curves of
Life (1914) was unable to define the "well known logarithmic
spiral"
equated in 1881 with the chemical elements (see the previous section: Spira
Solaris and the Three-fold number),
neither Canon Mosely14 nor
Thompson were
able write openly about the
either the
Golden Ratio or the Pheidian planorbidae. Nor unto the present day, it
seems have others, for if not a forbidden subject per se, it
long
seems to have been a poor career choice, so to speak. Moreover, even
after
Louis Agassiz introduced Benjamin Peirce's phyllotaxic approach to
structure of the Solar System in his Essay
on Classification
(1857) the matter was swiftly dispatched and rarely referred to again.
A possibly momentous shift in awareness, shunted aside with greatest of
ease, as the editor of
Essay on Classification, (E. Lurie)15
explained in the short loaded
footnote discussed in the
previous section.
Nor it would seem, were the
works of Arthur
Harry Church16 (On the Relation of
Phyllotaxis to Mechanical Law,
1904) or Samuel Colman17-18 (Nature's
Harmonic Unity,
1911) allowed
to take root. Nor again were the lines of inquiry laid out in
Jay Hambidge's19 Dynamic Symmetry
(1920) permitted to have
much on effect on the status quo either, not to mention Sir
Theodore Andrea Cook's Curves of Life
(1914) and the general
the thrust of the many papers published during the previous century and
on into the present.20-26
Where does this
obfuscation and
stagnation leaves us now?
Wondering
perhaps where we might be today if the implications of the phyllotactic
side of the matter introduced in 1850 by Benjamin Pierce had at
least been allowed to filter into the mainstream of knowledge with
its wider, all-inclusive perspective concerning "life" as we currently
understand it. The realization, perhaps, that we may indeed belong to
something larger than ourselves, and that as an integral, living part
of the Solar System rather than an isolated destructive apex,
that we should conduct ourselves with more care and consideration
towards all forms of life...."
All
living things are one, like the blood
which unites one family. All
of life forms one great web; man did not weave the Web of Life, he is
only a part of it. He is only a strand within it. Whatever he does to
the Web of Life he does to himself. ( The
Great Barrier Reef,
dir. Dr. George Casey, Science museum of Minnesota, 2001)27
Native wisdom tends to assign human beings enormous responsibility for sustaining harmonious relations within the whole natural world rather than granting them unbridled license to follow personal or economic whim ... Native wisdom sees spirit, however one defines that term, as dispersed throughout the cosmos or embodied in an inclusive, cosmos- sanctifying divine being. Spirit is not concentrated in a single, monotheistic Supreme Being ... Native spiritual and ecological knowledge has intrinsic value and worth, regardless of its resonances with or "confirmation" by modern Western scientific values.. (Peter Knudtson and David Suzuki, Wisdom of the Elders, 1992)
Here we surely need to come of age, and quickly.
Needless to say, there is much work to be done and many fences to be mended, but with a distinct focus and increased cooperation between Western and Arab scholars perhaps we may yet still build a few solid bridges towards a better and a more tolerant world.
spirasolaris
January 19, 2007
NOTES AND REFERENCES
- Agassiz, Louis. ESSAY ON CLASSIFICATION, Ed. E. Lurie, Belknap Press, Cambridge, 1962:131.
- Peirce, Benjamin. "Mathematical Investigations of the Fractions Which Occur in Phyllotaxis," Proceedings, AAAS, II 1850:444-447.
- Agassiz, Louis. ESSAY ON CLASSIFICATION, Ed. E. Lurie, Belknap Press, Cambridge, 1962:127.
- Called here IMO from Leverrier, M, "The Intra-Mercurial Planet Question," Nature 14 (1876) 533. [Anon.]
- Agassiz, Louis. ESSAY ON CLASSIFICATION, Ed. E. Lurie, Belknap Press, Cambridge, 1962:127.
- Peirce, Benjamin. Address
of
Professor Benjamin Peirce, President of the American
Association for
the Year 1853, on retiring from the duties of President. AAAS, 1853:6–7.
Source (JPG): The
Cornell Library Historical Mathematics Monographs. [ html version: Peirce1853 ]
- Concise Dictionary of Scientific Bibliography, Charles Scribner’s Sons, New York, 1981:540.
- Agassiz,
Louis. (Louis
Agassiz, ESSAY ON
CLASSIFICATION, Ed. E. Lurie, Belknap Press, Cambridge,
1962:127-128.
- Bretagnon, P and Jean-Louis Simon, Planetary Programs and Tables from -4000 to +2800, Willman-Bell, Inc. Richmond, 1986.
- Harris, John N. "Projectiles, Parabolas, and Velocity Expansions of the Laws of Planetary Motion " JRASC, Vol 83, No. 3, June 1989:207-218.
- Kappraff, Jay. CONNECTIONS : The Geometric Bridge between Art and Science, McGraw-Hill, Inc., New York, 1991:89-96.
- Thomson, Sir D'Arcy Wentworth. On Growth and Form, Cambridge University Press, Cambridge 1942; Dover Books, Minneola 1992.
- Cook, Sir Theodore Andrea. The Curves of Life, Dover, New York 1978; republication of the London (1914) edition.
- Mosely, Rev. H. "On the geometrical forms of turbinated and discoid shells," Phil. trans. Pt. 1. 1838:351-370.
- Lurie, E. (Ed.) Essay On Classification, Belknap Press, Cambridge 1962:128.
- Church, Arthur Harry. On The Relation of Phyllotaxis to Mechanical Law, Williams and Norgate, London 1904; also: http://www.sacredscience.com (cat #154).
- Colman, Samuel. Nature's
Harmonic
Unity, Benjamin Blom, New York 1971. Also:
- ___________ Harmonic Proportion and Form in Nature,
Art and Architecture, Dover, Mineola, 2003.
- Hambidge, Jay. Dynamic Symmetry,Yale University Press, New Haven 1920:16-18.
- It is
necessary to acknowledge the many positive strides made during the last
25 years, especially Roger V. Jean's Phyllotaxis:
A systemic study in plant
morphogenesis (1994) which by virtue of its scale and scope
invokes
the same admiration reserved for Sir D'Arcy Wentworth
Thompson's On
Growth and Form
(1917) and similar major works.
- Jean, Roger V. Phyllotaxis: A systemic study in plant morphogenesis, Cambridge University Press, Cambridge 1994.
- __________ Mathematical Approach to Pattern and Form in Plant Growth. Wiley, New York (1984).
- Kappraff, Jay. "The Spiral in Nature, Myth, and Mathematics" in Spiral Symmetry, Eds. István Hargittai and Clifford A. Pickover, World Scientific, Singapore, 1992.
- __________"The
relations between mathematics and mysticism of the golden mean through
history." In Fivefold Symmetry,
ed. I. Hargittai. World Scientific, Singapore, 1992: 33-65.
- Stewart, Ian. What Shape is a Snowflake,
Weidenfeld & Nicholson, London, 2001.
- Ghyka, Matila C. The Geometry of Art and Life,
Dover Publications, New York, 1977.
- Casey, George. The Great Barrier Reef, dir. Dr. George Casey, Science museum of Minnesota, 2001.
- Knudson, Peter and David Suzuki, Wisdom of the Elders, University of British Columbia Press, Vancouver, 1992.
- Menut, Albert D. and Alexander J. Denomy, Le Livre du ciel et du monde, University of Wisconsin Press, Madison 1968.
ASTRONOMICAL FRAMEWORK
QUANTIFICATION
AND QUALIFICATION I
THE GOLDEN SECTION AND THE STRUCTURE OF THE SOLAR SYSTEM
Spira
Solaris: Form and Phyllotaxis
I Bode's Flaw
http://www.spirasolaris.ca/sbb4a.html
Bode's "Law" - more correctly the Titius-Bode relationship - was an
ad hoc scheme for approximating mean planetary distances that was
originated by Johann Titius in 1866 and popularized by Johann Bode in
1871. The " law " later failed in the cases of the outermost
planets Neptune and Pluto, but it was flawed from the outset with
respect to distances of both MERCURY and EARTH, as Titius was perhaps
aware.
II The Alternative
http://www.spirasolaris.ca/sbb4b_07.html
Describes an alternative approach to the structure of the Solar System
that employs logarithmic data, orbital velocity, synodic motion, and
mean
planetary periods in contrast to ad hoc methodology and the use
of mean heliocentric distances alone.
III The Exponential
Order
http://www.spirasolaris.ca/sbb4c_07.html
The constant of linearity for the resulting planetary framework
is the
ubiquitous constant Phi known since antiquity. Major departures
from the theoretical norm are the ASTEROID BELT, NEPTUNE, and EARTH in
a resonant synodic position between VENUS and MARS.
Fibonacci/Golden Section Resonances in the Solar System.
Spira Solaris and
the plan-view of the Milky Way.
http://www.spirasolaris.ca/dfmilkyway.html
Last updated: March 13, 2007
QUANTIFICATION
AND QUALIFICATION II
GOLDEN SECTION SPIRALS IN NATURE, TIME AND PLACE
THE
THREE-FOLD NUMBER
IVd2b Spira Solaris and
the 3-Fold Number
http://www.spirasolaris.ca/sbb4d2b.html
The Spiral of Pheidias; Pheidian/Golden Spirals
Defined.
Pheidian Spirals and the Chemical Elements.
Notes on the
Logarithmic Spiral (Jay Hambidge; R. C. Archibald)
http://www.spirasolaris.ca/hambidge1a.html
R.C. Archibald's Golden
Bibliography.
The Whirlpool Galaxy (M51) (BW: 100kb)
http://www.spirasolaris.ca/m51abw.html
The Whirlpool Galaxy (M51)(Colour: 200kb)
http://www.spirasolaris.ca/m51.html
The Phyllotaxic
approach to the structure of the Solar System of Benjamin Pierce
(1750)
THE PHEIDIAN PLANORBIDAE
IVd2c Spira Solaris and
the Pheidian Planorbidae.
http://www.spirasolaris.ca/sbb4d2c.html
Applied to Nautiloid spirals, Ammonites, Snails and Seashells.
The
Phedian Planorbidae in Astronomical context; Orbital velocity, Mass and
Angular Momentum.
Ammonites and Seashells (Beginning excerpt).
http://www.spirasolaris.ca/sbb4d2cs.html
Whirling Rectangles
and The Golden Section (Animation I)
http://www.spirasolaris.ca/animation1.html
Whirling Rectangles
and The Golden Section (Animation II)
http://www.spirasolaris.ca/animation2.html
Appendix: The Matter of Lost
Light.
The understanding of Canon Mosely and Sir D'Arcy Wentworth Thompson.
Velocity
Expansions of
the
Laws of Planetary Motion.
http://www.spirasolaris.ca/sbb7a.html
Abstract
Kepler's Third Law of planetary motion: T2 = R3
(T = period in years, R = mean distance in astronomical
units) may be extended to include the inverse of the mean speed Vi (in
units
of the inverse of the Earth's mean orbital speed) such that: R = Vi2
and T2 = R3 = Vi 6. The first relation
- found in Galileo's last major work, the Dialogues Concerning Two
New
Sciences (1638) - may also be restated and expanded to include
relative
speed Vr (in units of Earth's mean orbital speed k) and absolute speed
Va
= kVr. This paper explains the context of Galileo's velocity expansions
of
the laws of planetary motion and applies these relationships to the
parameters
of the Solar System. A related "percussive origins" theory of planetary
formation is also discussed.
Note: This paper (which deals with the resurrection of the Fourth Law of Planetary Motion, i.e., the velocity component) was written north of the 70th parallel during the Summer of 1988.
It was subsequently published in the Journal of the Royal Astronomical Society of Canada (JRASC) the following year. It is reproduced here with the permission of the Editor of the Journal.
Times
Series Analysis.
http://www.spirasolaris.ca/time1.html
The advent of modern computers permits the investigation of planetary
motion
on an unprecedented scale. It is now feasible to treat single events
sequentially and apply detailed time-series analyses to the results.
Time Series Graphics
http://www.spirasolaris.ca/times2.html
Examples of chaotic
and resonant planetary relationships in the Solar System and
a possible link with Solar Activity.
Copyright © 1997. John N. Harris, M.A. (CMNS). This section last updated on July 28, 2004.